【基本】指数関数のグラフ

🕒 2018/06/14 🔄 2023/07/13

整数乗や有理数乗、無理数乗などを踏まえて、ここでは指数関数のグラフがどうなるかを見ていきます。

📘 目次

2のx乗のグラフ

ここでは、 $y=2^x$ の x にいろいろな値を入れて、グラフがどうなるかを見てみましょう。

まず、 $x=1,2,3$ のときは、 $y=2,4,8$ となります。また、 $x=0,-1,-2$ のときは、【基本】整数の指数で見たように、 $y=1,\dfrac{1}{2}, \dfrac{1}{4}$ となります。 $x$ が1減るごとに、 $y$ は $\dfrac{1}{2}$ 倍になっていくのでした。

さらに、 $x=\dfrac{1}{2},-\dfrac{1}{2}$ を考えると、【基本】有理数の指数で見たように、 $y=\sqrt{2},\dfrac{1}{\sqrt{2} }$ となるのでした。また、 $x=\dfrac{3}{2}$ なら、 $y=2^{\frac{3}{2} }=2\sqrt{2}$ となります。

これらをもとにいくつか点をとってみると、次のようになります。

さらに、 x が有理数のときの点を追加していくと、間の点が埋まっていきます。無理数のときの値も、近くの有理数の値を使って定義した（参考：【基本】実数の指数）ので、最終的に、 $y=2^x$ のグラフは、次のようになめらかにつながっていきます（先ほどの点に追加しています）。

また、左に1進むと $y$ は $\dfrac{1}{2}$ 倍になるので、左に行くほどどんどん小さくなり、 $0$ に近づいていきます。グラフでいえば、 x 軸に近づいていく、ということですね。

指数関数

先ほど、 $y=2^x$ のグラフを見ました。このような、 $y=a^x$ という形をした関数を、指数関数(exponential function) と言います。指数の部分に $x$ がある関数、ということですね。

なお、このとき、 $a$ には2つの条件が付きます。1つは、 $a\gt 0$ という条件です。これがないと、 $a^x$ が決まらないことがあるからです（例えば、 $a=-1,x=\dfrac{1}{2}$ のとき、 $y$ に対応する実数がない）。

2つ目の条件は、 $a\ne 1$ という条件です。 $a=1$ なら、 $a^x$ はつねに $1$ なので、そういう場合は外します。

今後、指数関数と言えば、 $a$ にあたる部分は、$1$ ではない正の実数、という条件で考えることにします。

なお、 $y=a^x$ の $a$ のことを底（てい、base）といいます。 $y=a^x$ を「 $a$ を底とする $x$ の指数関数」といいます。

先ほど見たグラフは、指数関数 $y=2^x$ のグラフ、ということになります。

他の指数関数のグラフ

$a$ をいろいろ変えて、 $y=a^x$ のグラフがどうなるかを考えてみましょう。

例えば、 $a=3$ のとき、 $y=3^x$ となります。このときも、 $x=0$ のときは $y=1$ なので、点 $(0,1)$ を通ることがわかります。ただ、 $x$ が1増えると $3$ 倍になり、 $x$ が1減ると $\dfrac{1}{3}$ 倍になることから、 $y=2^x$ のときと比べると、 y 軸の右側ではより大きく、左側ではより小さくなります。

よって、グラフは次のようになります。

次に、 $a=\dfrac{1}{2}$ のときを考えてみましょう。つまり、 $y=\left(\dfrac{1}{2}\right)^x$ ですね。このとき、 $x=-1,0,1$ とすると、 $y=2,1,\dfrac{1}{2}$ となります。 $y=2^x$ のときとは逆で、 x が1増えると $\dfrac{1}{2}$ 倍になり、 x が1減ると $2$ 倍になります。このことから、 $y=\left(\dfrac{1}{2}\right)^x$ は $y=2^x$ と左右対称なグラフとなります。

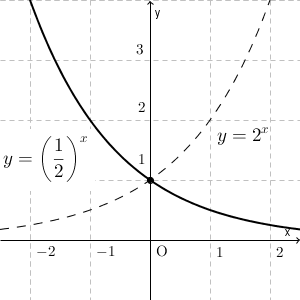
左右対称になることは、次のように変形してもわかるでしょう。
\begin{eqnarray} \left(\dfrac{1}{2}\right)^x &=& (2^{-1})^x \\ &=& 2^{-x} \end{eqnarray}こう書けば、 $y=2^x$ のグラフを y 軸で反転させれば $y=\left(\dfrac{1}{2}\right)^x$ のグラフになることがわかりやすいですね。

一般に、指数関数 $y=a^x$ について、 $x=0,1$ のときに $y=1,a$ であることから、グラフは、 $(0,1)$, $(1,a)$ の2点を通ることがわかります。

また、 $x$ が1増えれば $y$ は $a$ 倍に、1減れば $\dfrac{1}{a}$ 倍になることから、 $a\gt 1$ ならグラフは右肩上がり、 $a\lt 1$ ならグラフは右肩下がりの曲線になることがわかります。上のグラフの $a=2,\dfrac{1}{2}$ のときを見比べてもわかりますね。

$y$ の値はつねに正です。グラフから、いくらでも大きな値をとりえるし、0に近いどんな小さな値もとりえることがわかります。

$a$ の値に関わらず、グラフは x 軸に限りなく近づきます。このような線を漸近線といいます。つまり、指数関数のグラフは、 x 軸が漸近線となります。