【基本】指数関数の性質

ここでは、指数関数の大小関係に関する性質を見ていきます。

指数関数のグラフの復習

指数関数 $y=a^x$ のグラフの復習をしておきましょう（参考：【基本】指数関数のグラフ）。

指数関数のグラフは、底が $1$ より大きいときと小さいときとで大きく異なるのでした。まず、 $a\gt 1$ のときは、次のように、右肩上がりのグラフになります。具体的にいくつか点をとってみると、右肩上がりになることはわかると思います。

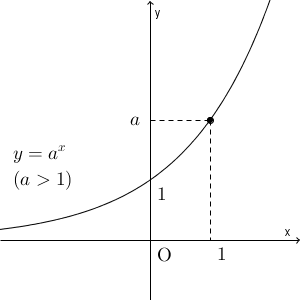
$0\lt a\lt 1$ のときは、逆に、右肩下がりのグラフになります。右に1進むと、 $y$ の値は $a$ 倍されるので、どんどん小さくなっていくからですね。グラフは次のようになります。

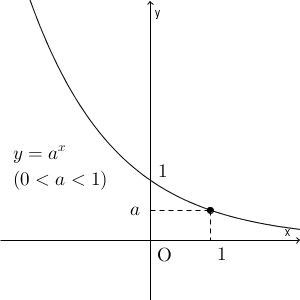
どちらの場合も、 $y$ の値はつねに正であり、正の値をすべてとりえます。また、 $x$ 軸が漸近線となります。

指数関数の大小関係

指数関数のグラフを踏まえて、指数関数の大小関係について考えてみましょう。

(1)は、すべて「3のなんとか乗」と書けそうですね。それぞれを、 $3^x$ の形で書きなおすと、それぞれ次のようになります。\[ 3^{\frac{1}{2} },\ 3^{\frac{2}{3} },\ 3^{\frac{3}{5} } \]このままだと指数の大小関係がわかりにくいので、指数の分母を30に合わせてみましょう。\[ 3^{\frac{15}{30} },\ 3^{\frac{20}{30} },\ 3^{\frac{18}{30} } \]こうすると、指数の大小関係がわかります。

ここで、 $y=3^x$ のグラフがどうなるかを考えてみましょう。底（ $y=a^x$ の $a$ の部分）は、 $3$ であり、 $1$ より大きいですね。なので、先ほど復習したように、グラフは右肩上がりになります。つまり、 $x$ が大きいほど $y$ も大きくなる、ということですね。

なので、指数が小さい順番に並べればいいので、\[ \sqrt{3},\ \sqrt[5]{27}, \ \sqrt[3]{9} \]が答えとなります。

(2)は、すべて、 $\dfrac{1}{2}$ のなんとか乗と書けそうだ、とわかるので、同じように書き直してみましょう。なお、先ほどと同じように、指数の分母は合わせておきます。\[ \left(\dfrac{1}{2}\right)^{\frac{15}{30} },\ \left(\dfrac{1}{2}\right)^{\frac{20}{30} }, \left(\dfrac{1}{2}\right)^{\frac{18}{30} } \]

指数の部分は先ほどと同じです。しかし、底の部分が異なります。底は $\dfrac{1}{2}$ なので $1$ より小さいです。そのため、先ほど復習したように、グラフは右肩下がりになります。つまり、 $x$ が大きいほど $y$ は小さくなります。

なので、指数が大きい順番に並べればいいので、\[ \sqrt[3]{\dfrac{1}{4} }, \ \sqrt[5]{\dfrac{1}{8} }, \ \sqrt{\dfrac{1}{2} } \]が答えとなります。

ここで見たように、底が $1$ より大きいのか小さいのか、という情報はとても重要です。これによってグラフの形状、大小関係がガラッと変わってしまうからです。指数関数を考えるときは、底が $1$ より大きいのか、小さいのかをつねに意識するようにしましょう。

おわりに

ここでは、指数関数のグラフについて復習した後、大小関係を考える問題を見ました。底の大きさに注意することを忘れないようにしましょう。