【標準】指数関数を含む関数の最大・最小
ここでは、指数関数を含む関数の最大値や最小値を求める問題を見ていきます。
指数関数を含む関数の最大・最小1
右辺には、底が異なる指数関数があるので、まずは底をそろえましょう。 $2$ で揃えれば、1つ目の項は、 $4^x=2^{2x}$ とできます。また、これから $2^x$ を1つにまとめたほうがよさそう、ということが予想できるので、2つ目の項も\[ 2^{x+2} = 4\cdot 2^x \]と変形します。こうすると、元の式は\[ y=2^{2x}-4\cdot 2^x+1 \]と変形できます。
ここで、 $t=2^x$ とおくと、この式は次のように変形できます。
\begin{eqnarray}
y
&=&
t^2-4t+1 \\[5pt]
&=&
(t-2)^2-3 \\[5pt]
\end{eqnarray}これは $t$ についての二次関数なので、あとはグラフをかいて考えればおしまいです。が、 $t$ はどういう値をとるかを考えていませんでした。
今、 $-2\leqq x \leqq 2$ であり、 $t=2^x$ とおいているのでした。底は $2$ で、 $1$ より大きいため、グラフは右肩上がりです。よって、 $t$ の範囲は\[ \dfrac{1}{4} \leqq t \leqq 4 \]となります。この範囲で、 $y=t^2-4t+1$ のグラフをかいてみます。
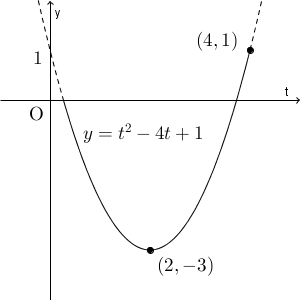
これより、 $t=2$ 、つまり、 $x=1$ のときに、最小値 $-3$ をとることがわかります。また、 $t=4$ 、つまり、 $x=2$ のときに、最大値 $1$ をとることがわかります。これらが答えです。
$t=a^x$ とおくときには、底が $1$ より大きいか小さいかに注意して、 $t$ の範囲がどうなるかを考える必要があります。定義域を確認してから、最大値・最小値を考えるようにします。
指数関数を含む関数の最大・最小2
$y$ の後半部分は、 $t$ を用いて簡単に置き換えることができます。問題は $4^x+4^{-x}$ の部分ですね。これは、 $t$ を2乗すれば、欲しいパーツが出てきます。
\begin{eqnarray}
t^2
&=&
(2^x+2^{-x})^2 \\[5pt]
&=&
2^{2x}+2\cdot 2^x \cdot 2^{-x}+2^{-2x} \\[5pt]
&=&
4^x+2+4^{-x} \\[5pt]
\end{eqnarray}となるので、\[ 4^x+4^{-x}=t^2-2 \]と変形することができます。なので、 $y$ を $t$ を用いて表すと
\begin{eqnarray}
y
&=&
(t^2-2)-2t \\[5pt]
&=&
t^2-2t-2 \\[5pt]
\end{eqnarray}となります。これが前半部分の答えです。
問題文には「 $t=2^x+2^{-x}$ とおきなさい」と書いていますが、書いていなくても、 $4^x+4^{-x}$ と $2^x+2^{-x}$ を見て、「 $t=2^x+2^{-x}$ とおけばよさそう」と思いつけるようになっておきましょう。
さて、後半部分ですが、今となっては、二次関数の最小値を求める問題になっています。平方完成をして
\begin{eqnarray}
y
&=&
t^2-2t-2 \\[5pt]
&=&
(t-1)^2-3 \\[5pt]
\end{eqnarray}となります。なので、「 $t=1$ のときに最小値 $3$ をとる」と思ってしまいそうですが、そうではありません。 $t$ の範囲を考えないといけません。
$t=2^x+2^{-x}$ とおいていました。 $2^x$ も $2^{-x}$ も、両方正だから、この和も正です。しかし、正の値すべてをとるわけではありません。これはとても重要です。
$y=2^x$ と $y=2^{-x}$ のグラフをかいてみると、次のようになります。
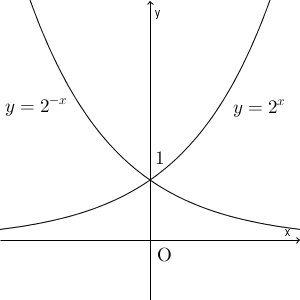
グラフを見てみると、 $x\gt 0$ のところでは $y=2^x$ はつねに $1$ より大きいです。また、 $x\lt 0$ のところでは、 $y=2^{-x}$ はつねに $1$ より大きいです。なので、 $t=2^x+2^{-x}$ は、つねに $1$ より大きく、「 $t=1$ のときに最小値をとる」なんてことはありえないことがわかります。 $t=1$ となることがないですからね。
では、 $t$ の範囲はどうなるかというと、思いつきにくいですが、相加・相乗平均の関係を使います(参考:【基本】相加・相乗平均の関係)。 $2^x,2^{-x}$ がともに正なので
\begin{eqnarray}
2^x+2^{-x} \geqq 2\sqrt{2^x\cdot2^{-x} } =2
\end{eqnarray}となります(等号は $2^x=2^{-x}$ のとき、つまり、 $x=0$ のときに成り立つ)。また、 $y=2^x$ も $y=2^{-x}$ も正の値をすべてとり得るので、 $t$ は2以上の値をすべてとり得ることがわかります。この $t\geqq 2$ の範囲で、関数の値を考えなければいけません。
$t\geqq 2$ の範囲で $y=t^2-2t-2$ のグラフをかくと、次のようになります。
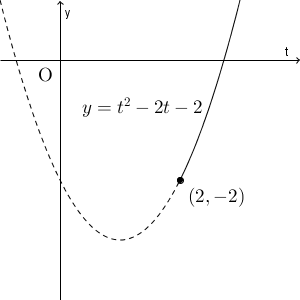
これより、 $t=2$ 、つまり、 $x=0$ のときに、 $y$ は最小値 $-2$ をとることがわかります。
$a\gt0,a\ne1$ のとき、 $a^x$ と $a^{-x}$ の和は、相加・相乗平均の関係から、 $2$ 以上になります。何度も使わないと思いつきにくいですが、掛けて $1$ になるものを足す場面では、よく使われます。
おわりに
ここでは、指数関数を含む関数の最大・最小を求める問題を見ました。指数関数の部分を別の文字で置き換えるときには、範囲がどうなるかに注意しましょう。





