【基本】関数の極限とはさみうちの原理

🕒 2018/08/25 🔄 2023/06/24

ここでは、大小関係のある複数の関数について、極限がどうなるかを見ていきます。また、三角関数の極限についても、少し触れておきます。

📘 目次

三角関数の極限

まず、三角関数のグラフを用いて、三角関数の極限を考えてみましょう（参考：【基本】三角関数のグラフ）。

$y=\sin \theta$ のグラフは次のようになります。

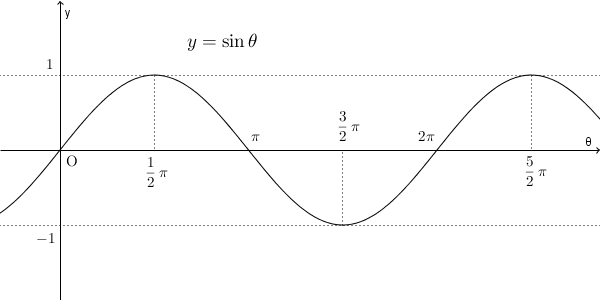
このグラフを見てもわかる通り、 $y=\sin \theta$ は $-1$ から $1$ までの値を繰り返しとり、一定の値はとりません。なので、 $\theta\to\infty$ や $\theta\to -\infty$ としたときの極限はありません。

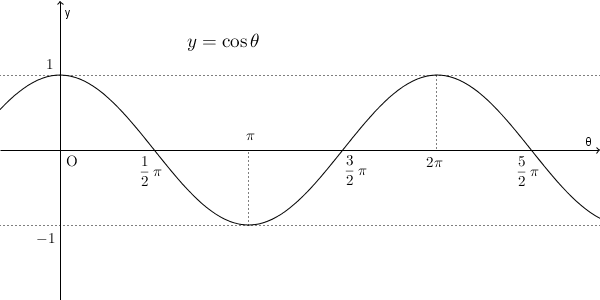
上のグラフは $y=\cos \theta$ のグラフですが、これも同様に、 $\theta\to\infty$ や $\theta\to -\infty$ としたときの極限はありません。

また、 $y=\tan \theta$ のグラフは次のようになります。

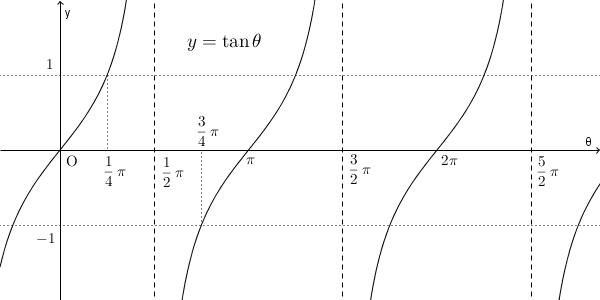
これも、 $\theta\to\infty$ や $\theta\to -\infty$ としたときの極限はありません。また、 $\theta\to\dfrac{\pi}{2}-0$ としたときの極限は正の無限大、 $\theta\to\dfrac{\pi}{2}+0$ としたときの極限は負の無限大なので、 $\theta\to\dfrac{\pi}{2}$ としたときの極限はありません。

こうしてみると、三角関数を使った極限はあまりなさそうな気がしてきますね。ただ、これから見ていくように、三角関数そのままの形ではなく、少し変形させた形で登場することになります。

関数の極限と大小関係

例題

次の極限を求めなさい。\[ \lim_{x\to\infty} \frac{\sin x}{x} \]

先ほども見た通り、分子は収束しません。なので、工夫をして極限を求める必要があります。

似たような極限を、【基本】数列の極限とはさみうちの原理のページで見ています。「 $\sin x$ の値は収束しないけれど、取りうる値の範囲は制限される」ことを利用していましたが、ここでもそのアイデアが使えます。

先ほどのグラフでも見ましたが、 $\sin x$ は $-1$ 以上 $1$ 以下の値しかとりません。なので、 $x$ が正のときは\[ -\frac{1}{x} \leqq \frac{\sin x}{x} \leqq \frac{1}{x} \]が成り立ちます。ここで、 $x\to \infty$ とすると、左の辺も右の辺も $0$ に収束します。なので、真ん中の辺も $0$ に収束するしかありません。よって、\[ \lim_{x\to\infty} \frac{\sin x}{x}=0 \]となります。

【基本】数列の極限とはさみうちの原理のページで見た、数列の極限と大小関係、はさみうちの原理は、関数の場合にも成り立ちます。関数の場合で書き直すと、次のようになります。

関数の極限と大小関係

関数 $f(x)$, $g(x)$ は、 $x$ が $a$ の近くで常に $f(x)\leqq g(x)$ であるとする。
このとき、 $\displaystyle\lim_{x\to a}f(x)=\alpha, \lim_{x\to a}g(x)=\beta$ ならば、 $\alpha\leqq \beta$ が成り立つ。
また、 $\displaystyle\lim_{x\to a} f(x)=\infty$ ならば、 $\displaystyle \lim_{x\to a}g(x)=\infty$ が成り立つ（追い出しの原理）。

「 $x$ が $a$ の近くで」というのは、 $x\to a$ の場合を考えるのだから、 $a$ のまわりだけで $f(x)\leqq g(x)$ が成り立っていればいい、すべての $x$ について成り立っていなくてもいい、ということです。

また、 $x$ が $a$ の近くでつねに $f(x)\lt g(x)$ だったとしても、上の式の $\alpha\leqq \beta$ はそのままです。 $\alpha\lt \beta$ が成り立つとは限りません。数列のときと同様に、イコールがつくことに注意しましょう。

はさみうちの原理（関数）

関数 $f(x)$, $g(x)$, $h(x)$ は、 $x$ が $a$ の近くで常に $f(x)\leqq h(x)\leqq g(x)$ を満たし、 $\displaystyle\lim_{x\to a}f(x)=\alpha, \lim_{x\to a}g(x)=\alpha$ となるならば、 $\displaystyle \lim_{x\to a}h(x)=\alpha$ となる。

同じ値に収束する関数に挟まれてしまったら、真ん中もその値に収束する、というのは、イメージしやすいと思います。 $\sin$ を $-1$ と $1$ ではさんで、はさみうちの原理から極限を求める、というのは、よく使う手法です。

また、先ほどの例題では、次のようにはさむ方法もよく使われます。\[ 0\leqq \frac{|\sin x|}{x} \leqq \frac{1}{x} \]$x$ が正のときは、これが成り立ちます。ここで、左端は常に $0$ で固定なので、右辺だけを考えればよくなるわけですね。極限を考える数が2つから1つに減るので、このように、片方を定数で固定してはさむ方法もよく使われます。

上で見た内容で、$x\to a$ の部分は、 $x\to \infty$ に置き換えても成り立ちます。その場合は、「 $x$ が $a$ の近くで」の部分は「 $x$ が十分大きい場合に」と読み替えればOKです。