【基本】関数の極限の性質

ここでは、整式で表される関数の極限を見ながら、関数の極限の性質を見ていきます。

整式と極限

これは、 $x$ を $2$ に近づけていったときに、 $x^2-x+1$ がどんな値に近づいていくか、を求める問題です。想像できる人もいるでしょうが、一応、グラフをかいて考えてみましょう。

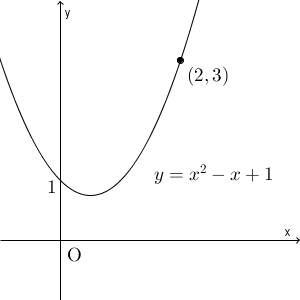
グラフは上のようになります。 $f(x)=x^2-x+1$ とすると、このグラフを見てもわかる通り、 $x$ を $2$ に近づけていけば、 $f(x)$ は $f(2)$ に近づいていくことがわかります。よって、極限は、\[ \lim_{x\to 2} (x^2-x+1)=2^2-2+1=3 \]となります。

このように、関数 $f(x)$ が整式で表されている場合（参考：【基本】整式とそれに関連する用語）、 $a$ が有限の値なら\[ \lim_{x\to a} f(x)=f(a) \]が成り立ちます。整式の場合は、極限を求めるのは難しくないですね。

簡単すぎて、「代入すればいいだけなのに、なんで極限なんて考えるんだ？」と思う人もいるかもしれませんが、安心してください、代入できない、難しい問題がこのあとたくさん出てきますので。

関数の極限の性質

今後、関数同士を足したり掛けたり割ったりしたときに、極限がどうなるかを考えたい場面が出てきます。【基本】数列の極限の性質で見たように、関数の場合も次の性質が成り立ちます。

これらは、整式で表された関数だけでなく、今後見ていくいろんな関数で成り立ちます。 $x\to a$ としたときに、 $f(x)\to\alpha$, $g(x)\to\beta$ となるのだから、どれも成り立つのは自然だと感じるでしょう。

高校数学の範囲では、これらを証明することはせず、イメージで「そりゃそうですよねぇ」という説明でおしまいです。大学数学では、極限の定義を厳密に行い、上の内容も証明することになるのですが、ここではそれはやめておきます。

上では、 $x\to a$ としたときの極限を考えていますが、 $x\to \infty$ や $x\to -\infty$ としたときの極限の場合も、収束するなら同じように成り立ちます。

数列のときもそうでしたが、「収束する」という条件はとても重要です。収束しない場合は、上のことは成り立ちません。

例えば、 $f(x)=\dfrac{1}{x^2}$, $g(x)=x^3$ として、 $x\to 0$ としたときの極限を考えてみると、 $f(x)$ は 正の無限大に発散、 $g(x)$ は $0$ に収束、となります。ここで、 $f(x)g(x)$ の極限を考えてみると、 $0$ に収束します。

$g(x)=x^2$ とすると、この場合も $g(x)$ は $0$ に収束しますが、 $f(x)g(x)$ は $1$ に収束します。つねに $1$ となるので、極限も $1$ になります。

$g(x)=x$ とすると、 $g(x)$ は $0$ に収束します。しかし、 $f(x)g(x)=\dfrac{1}{x}$ は収束しません。【基本】片側極限で見たように、右側極限（正の無限大）と左側極限（負の無限大）が一致しないので、極限を持ちません。

このように、収束しないものがあると、上で見た性質は使えず、極限はその都度工夫して求めなければいけません。特に、「∞ - ∞」、「∞ × 0」、「∞ ÷ ∞」、「0 ÷ 0」の形になってしまうものは、関数によって極限が変わってくるので、「不定形」と呼ばれています。このような場合にどう計算していくかは、今後様々な例を見ていくことになります。

おわりに

ここでは、整式で表される関数で、具体的に関数の極限を求めた後、関数の極限の性質を見ました。収束する場合は、足したり掛けたりした関数の極限を計算するのは難しくありませんが、収束しないものが含まれると工夫が必要になります。数列のところで見たテクニックも使いますし、それ以外の手法が必要になる場面もあるので、今後じっくり見ていくことにしましょう。