🏠 Home / 数学III / 関数と極限 / 関数の極限

【基本】指数関数の極限

🕒 2018/08/23 🔄 2023/06/24

ここでは、指数関数に関する極限について考えていきます。

📘 目次

指数関数の復習

指数関数の極限を考える前に、指数関数やそのグラフについて、少し復習しておきましょう。

【基本】指数関数のグラフや【基本】指数関数の性質で見たように、指数関数 $y=a^x$ のグラフは、 $a$ の値によって、大きく形が変わるのでした。

$a\gt 1$ のときは、 $y=a^x$ の値は、 $x$ が大きくなるほど大きく、小さくなるほど小さくなっていきます。

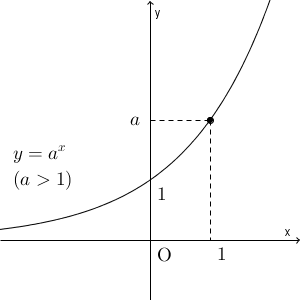
グラフは上のようになり、$a\gt 1$ のときは\[ \lim_{x\to \infty} a^x=\infty,\ \lim_{x\to -\infty} a^x=0 \]となります。

また、 $0\lt a \lt 1$ のときは、 $y=a^x$ の値は、 $x$ が大きくなるほど小さく、小さくなるほど大きくなります。

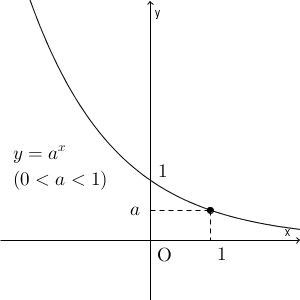
グラフは上のようになり、$0\lt a\lt 1$ のときは\[ \lim_{x\to \infty} a^x=0,\ \lim_{x\to -\infty} a^x=\infty \]となります。

これらを踏まえて、指数関数の極限を考えていきましょう。

指数関数の極限（そのまま代入）

例題1

次の極限を求めなさい。\[ \lim_{x\to 2} (3^x-2^{2x}) \]

先ほどのグラフを見てもわかる通り、 $x\to 2$ とすると、 $3^x$ は $3^2$ に近づいていきます。 $2^{2x}$ は $2^4$ に近づいていくので、\[ \lim_{x\to 2} (3^x-2^{2x}) = 3^2-2^4=-7 \]となります。

指数関数の極限（カッコでくくる）

例題2

次の極限を求めなさい。\[ \lim_{x\to \infty} (3^x-2^{2x}) \]

$3^x$, $2^{2x}$ の両方とも正の無限大に発散してしまうので、このままでは極限を考えることができません。ただ、今の場合は、両方とも底が $1$ より大きいので、「底が大きい方が、値が大きくなっていくスピードが速い」ことがわかります。このことから、極限を考えてみましょう。

$2^{2x}=4^x$ なので、 $3^x$ と $4^x$ なら、後者の方がはやく大きくなっていきます。このことをはっきり表すために、次のように変形してみます。
\begin{eqnarray} & & \lim_{x\to \infty} (3^x-2^{2x}) \\[5pt] &=& \lim_{x\to \infty} (3^x-4^x) \\[5pt] &=& \lim_{x\to \infty} 4^x\left\{\left(\frac{3}{4}\right)^x-1\right\} \\[5pt] \end{eqnarray}$\left(\dfrac{3}{4}\right)^x$ の部分は、底が $1$ より小さい正の数なので、 $x\to\infty$ とすると $0$ に収束します。よって、最後の式の波かっこの中は、 $-1$ に収束します。 $4^x$ は正の無限大に発散するので、全体としては、負の無限大に発散します。\[ \lim_{x\to \infty} (3^x-2^{2x})=-\infty \]となります。

指数関数の極限（分母分子を同じもので割る）

例題3

次の極限を求めなさい。\[ \lim_{x\to -\infty} \frac{3^x-2^{2x} }{3^{x+1}+2^{2x} } \]

底が $1$ より大きいので、指数関数の部分は、どれも $0$ に収束します。なので、分母も分子も $0$ に収束してしまうため、このままでは極限を求めることができません。ただ、例題2で見たように、底が違えば値が変化するスピードが違ってきます。このことに注目して考えていきましょう。

まずは、値の変化をわかりやすくするため、指数部分が $x$ となるように、次のように変形してみましょう。
\begin{eqnarray} & & \lim_{x\to -\infty} \frac{3^x-2^{2x} }{3^{x+1}+2^{2x} } \\[5pt] &=& \lim_{x\to -\infty} \frac{3^x-4^x}{3\cdot 3^x+4^x} \\[5pt] \end{eqnarray}$x\to -\infty$ としたとき、 $3^x$ よりも $4^x$ のほうが速く小さくなっていきます。このことがはっきりとわかるように、分母・分子を $3^x$ で割ってみましょう。\[ \lim_{x\to -\infty} \frac{1-\left(\frac{4}{3}\right)^x}{3+\left(\frac{4}{3}\right)^x} \]$\left(\dfrac{4}{3}\right)^x$ の部分は、底が $1$ より大きいので、 $x\to -\infty$ とすると $0$ に収束します。このことから、分母は $3$ に、分子は $1$ に収束するので、\[ \lim_{x\to -\infty} \frac{3^x-2^{2x} }{3^{x+1}+2^{2x} }=\frac{1}{3} \]となることがわかります。

$x\to -\infty$ だと考えにくい人は、【基本】無理関数の極限の最後で見たように、 $t=-x$ と置いて考えてみるのもいいでしょう。こう置いて、同じように変形していけば
\begin{eqnarray} & & \lim_{t\to \infty} \frac{3^{-t}-2^{-2t} }{3^{-t+1}+2^{-2t} } \\[5pt] &=& \lim_{t\to \infty} \frac{3^{-t}-4^{-t} }{3\cdot 3^{-t}+4^{-t} } \\[5pt] &=& \lim_{t\to \infty} \frac{1-\left(\frac{3}{4}\right)^t}{3+\left(\frac{3}{4}\right)^t} \\[5pt] &=& \frac{1}{3} \\[5pt] \end{eqnarray}と求めることもできます。底が正で $1$ より小さいので、 $t\to\infty$ としたときに $\left(\dfrac{3}{4}\right)^t\to 0$ となることを使っています。