共通テスト 数学II・数学B 2018年度プレテスト 第1問 [2] 解説

2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【必答問題】

問題編

問題

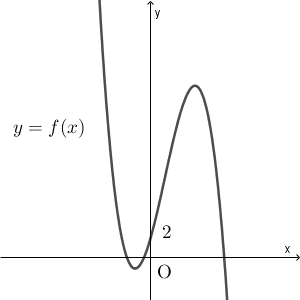
　3次関数 $f(x)$ は、 $x=-1$ で極小値 $-\dfrac{4}{3}$ をとり、 $x=3$ で極大値をとる。また、曲線 $y=f(x)$ は点 $(0,2)$ を通る。

(1) $f(x)$ の導関数 $f'(x)$ は $\myBox{カ}$ 次関数であり、 $f'(x)$ は\[ \left(x+\myBox{キ}\right)\left(x+\myBox{ク}\right) \]で割り切れる。

(2)
\begin{eqnarray} f(x)=\dfrac{\myBox{ケコ} }{\myBox{サ} }x^3+\myBox{シ}x^2+\myBox{ス}x+\myBox{セ} \end{eqnarray}である。

(3) 方程式 $f(x)=0$ は、三つの実数解をもち、そのうち負の解は $\myBox{ソ}$ 個である。

　また、 $f(x)=0$ の解を $a,b,c$ $(a\lt b\lt c)$ とし、曲線 $y=f(x)$ の $a\leqq x\leqq b$ の部分と $x$ 軸とで囲まれた図形の面積を $S$ 、曲線 $y=f(x)$ の $b\leqq x\leqq c$ の部分と $x$ 軸とで囲まれた図形の面積を $T$ とする。

　このとき\[ \int_a^c f(x)dx=\myBox{タ} \]である。 $\myBox{タ}$ に当てはまるものを、次の 0 ～ 8 のうちから一つ選べ。

　0: $0$
　1: $S$
　2: $T$
　3: $-S$
　4: $-T$
　5: $S+T$
　6: $S-T$
　7: $-S+T$
　8: $-S-T$

考え方

極値やグラフの通る点からもとの関数を求めるのは、微分積分の問題では典型的な問題です。

(3)の後半は、具体的な値が出てこないので考えにくいかもしれません。区間をわけて、どういう式で求められるかを考えてみましょう。

【必答問題】

解答編

問題

　3次関数 $f(x)$ は、 $x=-1$ で極小値 $-\dfrac{4}{3}$ をとり、 $x=3$ で極大値をとる。また、曲線 $y=f(x)$ は点 $(0,2)$ を通る。

(1) $f(x)$ の導関数 $f'(x)$ は $\myBox{カ}$ 次関数であり、 $f'(x)$ は\[ \left(x+\myBox{キ}\right)\left(x+\myBox{ク}\right) \]で割り切れる。

解説

3次関数を微分すると2次関数になります。また、 $x=-1,3$ で極値をとることから、 $f'(x)=0$ の解が $x=-1,3$ になるので、 $f'(x)$ は $(x+1)(x-3)$ で割り切れます。

解答

カキク：213

参考

【基本】極大値と極小値

解答編 つづき

問題

(2)
\begin{eqnarray} f(x)=\dfrac{\myBox{ケコ} }{\myBox{サ} }x^3+\myBox{シ}x^2+\myBox{ス}x+\myBox{セ} \end{eqnarray}である。

解説

$f'(x)$ は、定数 $a$ を使って、 $f'(x)=a(x+1)(x-3)$ と書けます。これより、 $f'(x)=a(x^2-2x-3)$ となります。

微分してこの関数になることから、 $f(x)$ はこれを積分すれば求められます。積分定数を $C$ とすると
\begin{eqnarray} f(x) &=& \int a(x^2-2x-3) dx \\[5pt] &=& a\left(\frac{x^3}{3}-x^2-3x\right)+C \end{eqnarray}となります。

曲線 $y=f(x)$ は 点 $(0,2)$ を通ることから、 $f(0)=2$ なので、 $C=2$ です。また、 $f(-1)=-\dfrac{4}{3}$ なので
\begin{eqnarray} f(-1) &=& -\dfrac{4}{3} \\[5pt] a\left\{\frac{(-1)^3}{3}-(-1)^2-3\cdot(-1)\right\}+2 &=& -\dfrac{4}{3} \\[5pt] \frac{5}{3}a &=& -\dfrac{10}{3} \\[5pt] a &=& -2 \\[5pt] \end{eqnarray}と求められます。

以上から
\begin{eqnarray} f(x) &=& -2\left(\frac{x^3}{3}-x^2-3x\right)+2 \\[5pt] &=& -\frac{2}{3}x^3+2x^2+6x+2 \\[5pt] \end{eqnarray}となります。

解答

ケコサシスセ：-23262

解答編 つづき

問題

(3) 方程式 $f(x)=0$ は、三つの実数解をもち、そのうち負の解は $\myBox{ソ}$ 個である。

解説

$x\leqq 0$ の範囲では、 $f(x)$ の値は次のように変化します。

$f(x)$ の値は、正の値から $-\dfrac{4}{3}$ まで減少し、その後 $2$ まで増加します。なので、 $f(x)=0$ となるタイミングは2回あるので、 $x\lt 0$ を満たす $f(x)=0$ の解は2つであることがわかります。

解答

ソ：2

解答編 つづき

問題

　また、 $f(x)=0$ の解を $a,b,c$ $(a\lt b\lt c)$ とし、曲線 $y=f(x)$ の $a\leqq x\leqq b$ の部分と $x$ 軸とで囲まれた図形の面積を $S$ 、曲線 $y=f(x)$ の $b\leqq x\leqq c$ の部分と $x$ 軸とで囲まれた図形の面積を $T$ とする。

　このとき\[ \int_a^c f(x)dx=\myBox{タ} \]である。 $\myBox{タ}$ に当てはまるものを、次の 0 ～ 8 のうちから一つ選べ。

　0: $0$
　1: $S$
　2: $T$
　3: $-S$
　4: $-T$
　5: $S+T$
　6: $S-T$
　7: $-S+T$
　8: $-S-T$

解説

$f(x)$ の値は、減少⇒増加⇒減少 と変化するので、 $a\leqq x\leqq b$ の範囲では $f(x)\leqq 0$ であり、 $b\leqq x\leqq c$ の範囲では $f(x)\geqq 0$ です。

なので、
\begin{eqnarray} S &=& -\int_a^b f(x) dx \\[5pt] T &=& \int_b^c f(x) dx \\[5pt] \end{eqnarray}であることから \begin{eqnarray} \int_a^c f(x) dx &=& \int_a^b f(x) dx + \int_b^c f(x) dx \\[5pt] &=& -S+T \end{eqnarray}となります。

解答

タ：7

参考

【基本】曲線とx軸の間の面積と積分