共通テスト 数学II・数学B 2018年度プレテスト 第5問 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【選択問題】(第3問~第5問から2問選択)
問題編
問題
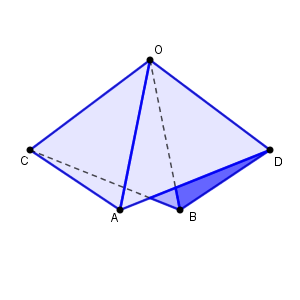
(1) 右の図のような立体を考える。ただし、六つの面 OAC, OBC, OAD, OBD, ABC, ABD は1辺の長さが $1$ の正三角形である。この立体の $\angle \mathrm{ COD }$ の大きさを調べたい。
線分 AB の中点を M、線分 CD の中点を N とおく。
$\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$, $\overrightarrow{ \mathrm{ OC } }=\vec{c}$, $\overrightarrow{ \mathrm{ OD } }=\vec{d}$ とおくとき、次の問いに答えよ。
(i) 次の $\myBox{ア}$ ~ $\myBox{エ}$ に当てはまる数を求めよ。
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OM } }=\dfrac{\myBox{ア} }{\myBox{イ} }\ (\vec{a}+\vec{b}) \\[5pt] & & \overrightarrow{ \mathrm{ ON } }=\dfrac{\mybox{ア} }{\mybox{イ} }\ (\vec{c}+\vec{d}) \\[5pt] & & \vec{a}\cdot\vec{b} = \vec{a}\cdot\vec{c} = \vec{a}\cdot\vec{d} = \vec{b}\cdot\vec{c} = \vec{b}\cdot\vec{d} =\dfrac{\myBox{ウ} }{\myBox{エ} } \\[5pt] \end{eqnarray}(ii) 3点 O, N, M は同一直線上にある。内積 $\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ CN } }$ の値を用いて、 $\overrightarrow{ \mathrm{ ON } }=k\overrightarrow{ \mathrm{ OM } }$ を満たす $k$ の値を求めよ。\[ k=\dfrac{\myBox{オ} }{\myBox{カ} } \]
(iii) $\angle \mathrm{ COD }=\theta$ とおき、 $\cos\theta$ の値を求めたい。次の方針1または方針2について、 $\myBox{キ}$ ~ $\myBox{シ}$ に当てはまる数を求めよ。
方針1
$\vec{d}$ を $\vec{a}$, $\vec{b}$, $\vec{c}$ を用いて表すと、\[ \vec{d}=\dfrac{\myBox{キ} }{\myBox{ク} }\vec{a} +\dfrac{\myBox{ケ} }{\myBox{コ} }\vec{b} -\vec{c} \]であり、 $\vec{c}\cdot\vec{d}=\cos\theta$ から $\cos\theta$ が求められる。方針2
$\overrightarrow{ \mathrm{ OM } }$ と $\overrightarrow{ \mathrm{ ON } }$ のなす角を考えると、 $\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } }=|\overrightarrow{ \mathrm{ OM } }|\ |\overrightarrow{ \mathrm{ ON } }|$ が成り立つ。 $|\overrightarrow{ \mathrm{ ON } }|^2 = \dfrac{\myBox{サ} }{\myBox{シ} }+\dfrac{1}{2}\cos\theta$ であるから、 $\overrightarrow{ \mathrm{ OM } }\cdot \overrightarrow{ \mathrm{ ON } }$, $|\overrightarrow{ \mathrm{ OM } }|$ の値を用いると、 $\cos\theta$ が求められる。(iv) 方針1または方針2を用いて $\cos\theta$ の値を求めよ。\[ \cos\theta=\dfrac{\myBox{スセ} }{\myBox{ソ} } \]
(2) (1) の図形から、四つの面 OAC, OBC, OAD, OBD だけを使って、下のような図形を作成したところ、この図形は $\angle \mathrm{ AOB }$ を変化させると、それにともなって $\angle \mathrm{ COD }$ も変化することがわかった。
$\angle \mathrm{ AOB }=\alpha$, $\angle \mathrm{ COD }=\beta$ とおき、 $\alpha\gt 0$, $\beta\gt 0$ とする。このときも、線分 AB の中点と線分 CD の中点および点 O は一直線上にある。
(i) $\alpha$ と $\beta$ が満たす関係式は(1)の方針2を用いると求めることができる。その関係式として正しいものを、次の 0 ~ 4 のうちから一つ選べ。 $\myBox{タ}$
0: $\cos\alpha+\cos\beta=1$
1: $(1+\cos\alpha)(1+\cos\beta)=1$
2: $(1+\cos\alpha)(1+\cos\beta)=-1$
3: $(1+2\cos\alpha)(1+2\cos\beta)=\dfrac{2}{3}$
4: $(1-\cos\alpha)(1-\cos\beta)=\dfrac{2}{3}$
(ii) $\alpha=\beta$ のとき、 $\alpha=\myBox{チツ}\ ^{\circ}$ であり、このとき、点 D は $\myBox{テ}$ にある。 $\myBox{チツ}$ に当てはまる数を求めよ。また、 $\myBox{テ}$ に当てはまるものを、次の 0 ~ 2 のうちから一つ選べ。
0: 平面 ABC に関して O と同じ側
1: 平面 ABC 上
2: 平面 ABC に関して O と異なる側
考え方
ベクトルについて理解していることはもちろん、空間や図形の把握能力も問われています。さらに、後半は前半と何が違うかを把握したうえで、どの計算や考え方が使い回せるか、どの部分を新しく考えないといけないのかを、正しく認識しなくてはならず、全体的に難しい内容になっています。
前問までで求めた内容のうち、どれを使うといいのかを考えて解いていきましょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
(1) 右の図のような立体を考える。ただし、六つの面 OAC, OBC, OAD, OBD, ABC, ABD は1辺の長さが $1$ の正三角形である。この立体の $\angle \mathrm{ COD }$ の大きさを調べたい。
線分 AB の中点を M、線分 CD の中点を N とおく。
$\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$, $\overrightarrow{ \mathrm{ OC } }=\vec{c}$, $\overrightarrow{ \mathrm{ OD } }=\vec{d}$ とおくとき、次の問いに答えよ。
(i) 次の $\myBox{ア}$ ~ $\myBox{エ}$ に当てはまる数を求めよ。
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OM } }=\dfrac{\myBox{ア} }{\myBox{イ} }\ (\vec{a}+\vec{b}) \\[5pt] & & \overrightarrow{ \mathrm{ ON } }=\dfrac{\mybox{ア} }{\mybox{イ} }\ (\vec{c}+\vec{d}) \\[5pt] & & \vec{a}\cdot\vec{b} = \vec{a}\cdot\vec{c} = \vec{a}\cdot\vec{d} = \vec{b}\cdot\vec{c} = \vec{b}\cdot\vec{d} =\dfrac{\myBox{ウ} }{\myBox{エ} } \\[5pt] \end{eqnarray}
解説
図形は、2つの正四面体をくっつけたものです。
M は線分 AB の中点なので\[ \overrightarrow{ \mathrm{ OM } }=\frac{\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ OB } } }{2}=\frac{1}{2}(\vec{a}+\vec{b}) \]が成り立ちます。
N は線分 CD の中点なので\[ \overrightarrow{ \mathrm{ ON } }=\frac{\overrightarrow{ \mathrm{ OC } }+\overrightarrow{ \mathrm{ OD } } }{2}=\frac{1}{2}(\vec{c}+\vec{d}) \]が成り立ちます。
また、三角形 OAB はすべての辺の長さが $1$ なので正三角形です。このことから
\begin{eqnarray}
\vec{a}\cdot\vec{b}=1\cdot1\cdot\cos 60^{\circ}=\frac{1}{2}
\end{eqnarray}となります。他の面も正三角形なので、同じように計算すれば、 $\vec{a}\cdot\vec{c}$, $\vec{a}\cdot\vec{d}$, $\vec{b}\cdot\vec{c}$, $\vec{b}\cdot\vec{d}$ は、どれも $\dfrac{1}{2}$ だとわかります。
解答
アイウエ:1212
解答編 つづき
問題
(ii) 3点 O, N, M は同一直線上にある。内積 $\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ CN } }$ の値を用いて、 $\overrightarrow{ \mathrm{ ON } }=k\overrightarrow{ \mathrm{ OM } }$ を満たす $k$ の値を求めよ。\[ k=\dfrac{\myBox{オ} }{\myBox{カ} } \]
解説
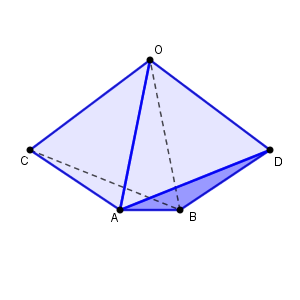
図形の対称性から、線分 CD の中点 N は、三角形 OAB 上にあり、さらに、線分 OM 上にあることもわかります。
また、直線 CD は、平面 OAB に垂直であることもわかります。
以上から、 $\overrightarrow{ \mathrm{ ON } }=k\overrightarrow{ \mathrm{ OM } }$ とおくことができ、 $\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ CN } }=0$ が成り立ちます。
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ CN } } \\[5pt]
&=&
\vec{a}\cdot \left( k\overrightarrow{ \mathrm{ OM } } -\vec{c} \right) \\[5pt]
&=&
\frac{k}{2}\vec{a}\cdot\vec{a}+\frac{k}{2}\vec{a}\cdot\vec{b}-\vec{a}\cdot\vec{c} \\[5pt]
&=&
\frac{k}{2}+\frac{k}{4}-\frac{1}{2} \\[5pt]
&=&
\frac{3k}{4}-\frac{1}{2} \\[5pt]
\end{eqnarray}が $0$ になるので、 $k=\dfrac{2}{3}$ だとわかります。
問題文の通りに解けばこのようになりますが、点 C 側からこの図形を見ると、もっと簡単に求められます。
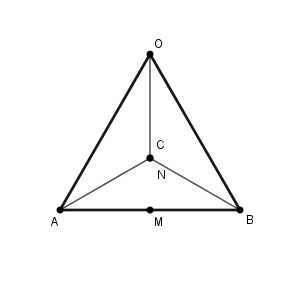
正三角形 OAB の重心が N で、辺AB の中点が M なので、重心の性質から\[ \overrightarrow{ \mathrm{ ON } }=\frac{2}{3}\overrightarrow{ \mathrm{ OM } } \]と求めることもできます。
解答
オカ:23
解答編 つづき
問題
(iii) $\angle \mathrm{ COD }=\theta$ とおき、 $\cos\theta$ の値を求めたい。次の方針1または方針2について、 $\myBox{キ}$ ~ $\myBox{シ}$ に当てはまる数を求めよ。
方針1
$\vec{d}$ を $\vec{a}$, $\vec{b}$, $\vec{c}$ を用いて表すと、\[ \vec{d}=\dfrac{\myBox{キ} }{\myBox{ク} }\vec{a} +\dfrac{\myBox{ケ} }{\myBox{コ} }\vec{b} -\vec{c} \]であり、 $\vec{c}\cdot\vec{d}=\cos\theta$ から $\cos\theta$ が求められる。方針2
$\overrightarrow{ \mathrm{ OM } }$ と $\overrightarrow{ \mathrm{ ON } }$ のなす角を考えると、 $\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } }=|\overrightarrow{ \mathrm{ OM } }|\ |\overrightarrow{ \mathrm{ ON } }|$ が成り立つ。 $|\overrightarrow{ \mathrm{ ON } }|^2 = \dfrac{\myBox{サ} }{\myBox{シ} }+\dfrac{1}{2}\cos\theta$ であるから、 $\overrightarrow{ \mathrm{ OM } }\cdot \overrightarrow{ \mathrm{ ON } }$, $|\overrightarrow{ \mathrm{ OM } }|$ の値を用いると、 $\cos\theta$ が求められる。
解説
方針1を考えます。先ほど $\overrightarrow{ \mathrm{ ON } }=\frac{2}{3}\overrightarrow{ \mathrm{ OM } }$ とわかったので、
\begin{eqnarray}
\overrightarrow{ \mathrm{ ON } } &=& \frac{2}{3} \overrightarrow{ \mathrm{ OM } } \\[5pt]
\frac{1}{2}(\vec{c}+\vec{d}) &=& \frac{2}{3} \cdot \frac{1}{2}(\vec{a}+\vec{b}) \\[5pt]
\vec{d}
&=&
\frac{2}{3}\vec{a}+\frac{2}{3}\vec{b}-\vec{c} \\[5pt]
\end{eqnarray}となります。
次に、方針2を考えます。
\begin{eqnarray}
|\overrightarrow{ \mathrm{ ON } }|^2
&=&
\left| \frac{1}{2}(\vec{c}+\vec{d}) \right|^2 \\[5pt]
&=&
\frac{1}{4}+\frac{1}{2}\vec{c}\cdot\vec{d}+\frac{1}{4} \\[5pt]
&=&
\frac{1}{2}+\frac{1}{2}\cos\theta \\[5pt]
\end{eqnarray}となります。
もしくは、次のようにして図形的に考えることも可能です。三角形 OCN は直角三角形なので、 ON の長さは $\cos\dfrac{\theta}{2}$ です。半角の公式から
\begin{eqnarray}
\cos^2\dfrac{\theta}{2} &=& \frac{\cos\theta+1}{2}
\end{eqnarray}なので、\[ |\overrightarrow{ \mathrm{ ON } }|^2=\frac{1}{2}+\frac{1}{2}\cos\theta \]となります。
解答
キクケコ:2323
サシ:12
解答編 つづき
問題
(iv) 方針1または方針2を用いて $\cos\theta$ の値を求めよ。\[ \cos\theta=\dfrac{\myBox{スセ} }{\myBox{ソ} } \]
解説
まずは、方針1で求めてみます。
\begin{eqnarray}
& &
\vec{c}\cdot\vec{d} \\[5pt]
&=&
\vec{c}\cdot \left(\frac{2}{3}\vec{a}+\frac{2}{3}\vec{b}-\vec{c}\right) \\[5pt]
&=&
\frac{2}{3}\vec{c}\cdot\vec{a}+\frac{2}{3}\vec{c}\cdot\vec{b}-\vec{c}\cdot\vec{c} \\[5pt]
&=&
\frac{2}{3}\cdot\frac{1}{2}+\frac{2}{3}\cdot\frac{1}{2}-1 \\[5pt]
&=&
-\frac{1}{3}
\end{eqnarray}と求められます。
方針2でも求めてみましょう。 O, N, M はこの順に同一直線上にあるので、 $\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } }$ は $|\overrightarrow{ \mathrm{ OM } }|\ |\overrightarrow{ \mathrm{ ON } }|$ と等しくなります。問題文に沿って計算すると
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } } \\[5pt]
&=&
\frac{1}{2}(\vec{a}+\vec{b}) \cdot \frac{1}{2}(\vec{c}+\vec{d}) \\[5pt]
&=&
\frac{1}{4} \left( \vec{a}\cdot\vec{c}+\vec{a}\cdot\vec{d}+\vec{b}\cdot\vec{c}+\vec{b}\cdot\vec{d}\right) \\[5pt]
&=&
\frac{1}{4} \times \frac{1}{2} \times 4 \\[5pt]
&=&
\frac{1}{2}
\end{eqnarray}となります。また、 $|\overrightarrow{ \mathrm{ OM } }|$ は、1辺が $1$ の正三角形の高さなので、 $\dfrac{\sqrt{3} }{2}$ です。以上から
\begin{eqnarray}
\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } } &=& |\overrightarrow{ \mathrm{ OM } }|\ |\overrightarrow{ \mathrm{ ON } }| \\[5pt]
\frac{1}{2} &=& \frac{\sqrt{3} }{2} |\overrightarrow{ \mathrm{ ON } }| \\[5pt]
|\overrightarrow{ \mathrm{ ON } }| &=& \frac{1}{\sqrt{3} }
\end{eqnarray}と求められます。
問題文に沿って求めるとこうなりますが、そもそも、 $\overrightarrow{ \mathrm{ ON } }=\frac{2}{3}\overrightarrow{ \mathrm{ OM } }$ なので、 $|\overrightarrow{ \mathrm{ ON } }|=\dfrac{\sqrt{3} }{3}$ と求めることも可能です。
この結果を使えば、
\begin{eqnarray}
|\overrightarrow{ \mathrm{ ON } }|^2 &=& \frac{1}{2}+\dfrac{1}{2}\cos\theta \\[5pt]
\frac{1}{3} &=& \frac{1}{2}+\dfrac{1}{2}\cos\theta \\[5pt]
\cos\theta &=& -\frac{1}{3} \\[5pt]
\end{eqnarray}と求められます。
解答
スセソ:-13
解答編 つづき
問題
(2) (1) の図形から、四つの面 OAC, OBC, OAD, OBD だけを使って、下のような図形を作成したところ、この図形は $\angle \mathrm{ AOB }$ を変化させると、それにともなって $\angle \mathrm{ COD }$ も変化することがわかった。
$\angle \mathrm{ AOB }=\alpha$, $\angle \mathrm{ COD }=\beta$ とおき、 $\alpha\gt 0$, $\beta\gt 0$ とする。このときも、線分 AB の中点と線分 CD の中点および点 O は一直線上にある。
(i) $\alpha$ と $\beta$ が満たす関係式は(1)の方針2を用いると求めることができる。その関係式として正しいものを、次の 0 ~ 4 のうちから一つ選べ。 $\myBox{タ}$
0: $\cos\alpha+\cos\beta=1$
1: $(1+\cos\alpha)(1+\cos\beta)=1$
2: $(1+\cos\alpha)(1+\cos\beta)=-1$
3: $(1+2\cos\alpha)(1+2\cos\beta)=\dfrac{2}{3}$
4: $(1-\cos\alpha)(1-\cos\beta)=\dfrac{2}{3}$
解説
(1)と同じように、図形の対称性から、N が三角形OAB 上にあること、さらに、OM 上にあることがわかります。そのため、 $\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } }=|\overrightarrow{ \mathrm{ OM } }|\ |\overrightarrow{ \mathrm{ ON } }|$ が成り立ちます。
$\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } }$ の値は、 $\frac{1}{2}(\vec{a}+\vec{b}) \cdot \frac{1}{2}(\vec{c}+\vec{d})$ ですが、これは(1)(iv) で求めたときと同じ計算で $\dfrac{1}{2}$ となります。
また、
\begin{eqnarray}
& &
|\overrightarrow{ \mathrm{ OM } }|^2 \\[5pt]
&=&
\frac{1}{4} (|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2) \\[5pt]
&=&
\frac{1}{2} (1+\cos\alpha) \\[5pt]
\end{eqnarray}と
\begin{eqnarray}
& &
|\overrightarrow{ \mathrm{ ON } }|^2 \\[5pt]
&=&
\frac{1}{4} (|\vec{c}|^2+2\vec{c}\cdot\vec{d}+|\vec{d}|^2) \\[5pt]
&=&
\frac{1}{2} (1+\cos\beta) \\[5pt]
\end{eqnarray}が成り立ちます。
以上から、
\begin{eqnarray}
|\overrightarrow{ \mathrm{ OM } }|^2\ |\overrightarrow{ \mathrm{ ON } }|^2 &=& (\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } })^2 \\[5pt]
\frac{1}{2} (1+\cos\alpha)\cdot \frac{1}{2} (1+\cos\beta) &=& \frac{1}{4} \\[5pt]
(1+\cos\alpha)(1+\cos\beta) &=& 1 \\[5pt]
\end{eqnarray}が成り立ちます。
なお、図形的に考えることもできます。三角形 OAM で考えると、この三角形は直角三角形なので\[ \mathrm{ OM }=\cos\dfrac{\beta}{2} \]が成り立ちます。また、直角三角形 OCN について考えると\[ \mathrm{ ON }=\cos\dfrac{\alpha}{2} \]が成り立ちます。
以上から、
\begin{eqnarray}
|\overrightarrow{ \mathrm{ OM } }|^2\ |\overrightarrow{ \mathrm{ ON } }|^2 &=& (\overrightarrow{ \mathrm{ OM } }\cdot\overrightarrow{ \mathrm{ ON } })^2 \\[5pt]
\cos^2\dfrac{\alpha}{2} \cdot \cos^2\dfrac{\beta}{2}&=& \frac{1}{4} \\[5pt]
\frac{\cos\alpha+1}{2} \cdot \frac{\cos\beta+1}{2} &=& \frac{1}{4} \\[5pt]
(1+\cos\alpha)(1+\cos\beta) &=& 1 \\[5pt]
\end{eqnarray}が成り立ちます。
ちなみに、(1)は、 $\cos\angle \mathrm{ AOB }=\dfrac{1}{2}$, $\cos\angle \mathrm{ COD }=-\dfrac{1}{3}$ の場合に対応します。これらの値を代入して成り立つかどうかも確認しておくといいでしょう。
解答
タ:1
解答編 つづき
問題
(ii) $\alpha=\beta$ のとき、 $\alpha=\myBox{チツ}\ ^{\circ}$ であり、このとき、点 D は $\myBox{テ}$ にある。 $\myBox{チツ}$ に当てはまる数を求めよ。また、 $\myBox{テ}$ に当てはまるものを、次の 0 ~ 2 のうちから一つ選べ。
0: 平面 ABC に関して O と同じ側
1: 平面 ABC 上
2: 平面 ABC に関して O と異なる側
解説
$\alpha=\beta$ のとき、 $(1+\cos\alpha)^2=1$ が成り立つから、 $\cos\alpha=0$ 、つまり、 $\alpha=90^{\circ}$ となります。
このとき、 OM も ON も長さが $\dfrac{\sqrt{2} }{2}$ となるので、 M と N は一致します。線分 AB と線分 CD の中点が一致するので、この4点は同一平面上にあることがわかります。
なお、このときの図形は、正八面体を半分に切ったものになります。
解答
チツ:90
テ:1