共通テスト 数学II・数学B 2018年度プレテスト 第1問 [3] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
$\log_{10}2=0.3010$ とする。このとき、 $10^{\myBox{チ} }=2$, $2^{\myBox{ツ} }=10$ となる。 $\myBox{チ}$, $\myBox{ツ}$ に当てはまるものを、次の 0 ~ 8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $0$
1: $0.3010$
2: $-0.3010$
3: $0.6990$
4: $-0.6990$
5: $\dfrac{1}{0.3010}$
6: $-\dfrac{1}{0.3010}$
7: $\dfrac{1}{0.6990}$
8: $-\dfrac{1}{0.6990}$
(2) 次のようにして対数ものさしAを作る。
対数ものさしA 2以上の整数 $n$ のそれぞれに対して、1の目盛りから右に $\log_{10}n$ だけ離れた場所に $n$ の目盛りを書く。
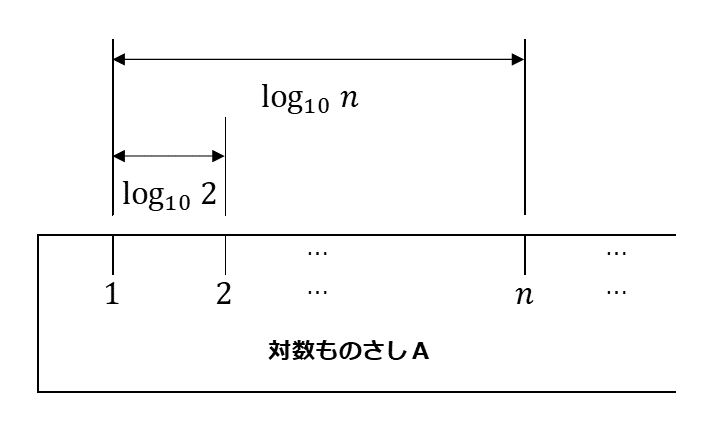
(i) 対数ものさしAにおいて、3の目盛りと4の目盛りの間隔は、1の目盛りと2の目盛りの間隔 $\myBox{テ}$ 。 $\myBox{テ}$ に当てはまるものを、次の 0 ~ 2 のうちから一つ選べ。
0: より大きい
1: に等しい
2: より小さい
また、次のようにして対数ものさしBを作る。
対数ものさしB 2以上の整数 $n$ のそれぞれに対して、1の目盛りから左に $\log_{10}n$ だけ離れた場所に $n$ の目盛りを書く。
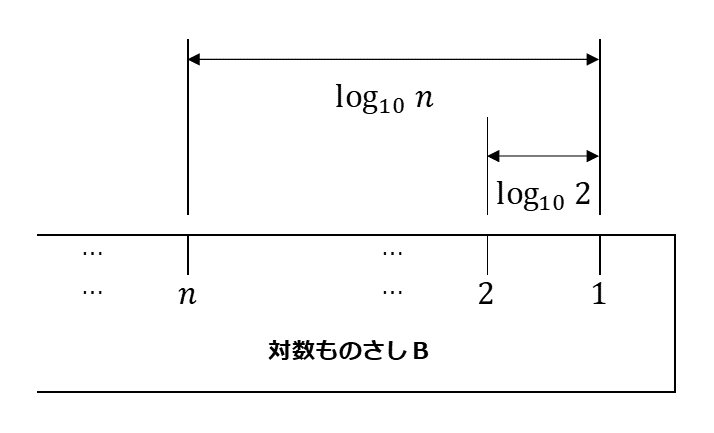
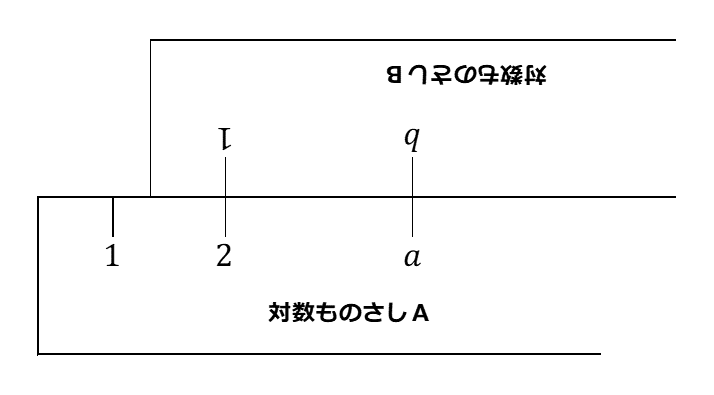
(ii) 次の図にように、対数ものさしAの2の目盛りと対数ものさしBの1の目盛りを合わせた。このとき、対数ものさしBの $b$ の目盛りに対応する対数ものさしAの目盛りは $a$ になった。
$a$ と $b$ の関係について、いつでも成り立つ式を、次の 0 ~ 3 のうちから一つ選べ。 $\myBox{ト}$
0: $a=b+2$
1: $a=2b$
2: $a=\log_{10}(b+2)$
3: $a=\log_{10}2b$
さらに、次のようにしてものさしCを作る。
ものさしC 自然数 $n$ のそれぞれに対して、 0 の目盛りから左に $n\log_{10}2$ だけ離れた場所に $n$ の目盛りを書く。
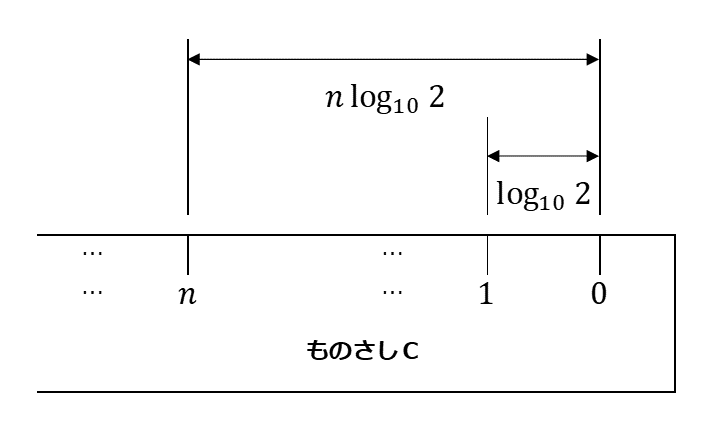
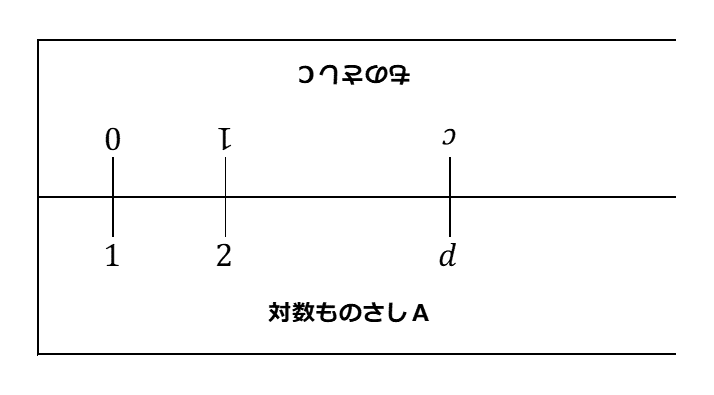
(iii) 次の図のように対数ものさしAの1の目盛りとものさしCの 0 の目盛りを合わせた。このとき、ものさしCの $c$ の目盛りに対応する対数ものさしAの目盛りは $d$ になった。
$c$ と $d$ の関係について、いつでも成り立つ式を、次の 0 ~ 3 のうちから一つ選べ。 $\myBox{ナ}$
0: $d=2c$
1: $d=c^2$
2: $d=2^c$
3: $c=\log_{10}d$
(iv) 対数ものさしAと対数ものさしBの目盛りを一度だけ合わせるか、対数ものさしAとものさしCの目盛りを一度だけ合わせることにする。このとき、適切な箇所の目盛りを読み取るだけで実行できるものを、次の 0 ~ 5 のうちからすべて選べ。 $\myBox{ニ}$
0: $17$ に $9$ を足すこと。
1: $23$ から $15$ を引くこと。
2: $13$ に $4$ をかけること。
3: $63$ を $9$ で割ること。
4: $2$ を $4$ 乗すること。
5: $\log_2 64$ の値を求めること。
考え方
対数ものさしを使った問題です。これは実際にあるものですが、この存在を知らなくても解ける問題になっています。とはいえ、初めて聞いて最後まで解ききるのはなかなか大変です。
(2)の(iii)までは、対数ものさしを使って、どのような値が計算できるかを確認する問題です。(i)で2つの目盛りの間隔が問われていますが、(ii)も(iii)も目盛りの間隔に着目して考えます。
最後の(iv)は、(ii)(iii)で得られた内容を応用して考えていきます。ただ、全部正しく答えるのは相当難しいです。(iv)の正答率は 1.3% とのことです。
解答編
問題
$\log_{10}2=0.3010$ とする。このとき、 $10^{\myBox{チ} }=2$, $2^{\myBox{ツ} }=10$ となる。 $\myBox{チ}$, $\myBox{ツ}$ に当てはまるものを、次の 0 ~ 8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $0$
1: $0.3010$
2: $-0.3010$
3: $0.6990$
4: $-0.6990$
5: $\dfrac{1}{0.3010}$
6: $-\dfrac{1}{0.3010}$
7: $\dfrac{1}{0.6990}$
8: $-\dfrac{1}{0.6990}$
解説
$\log_{10}2$ とは、 $10^{x}=2$ を満たす $x$ のことです。なので、 $\log_{10}2=0.3010$ であることを使って、 $10^{0.3010}=2$ となります。
この両辺を $\dfrac{1}{0.3010}$ 乗すると、左辺は $(10^{0.3010})^{\frac{1}{0.3010} }=10^1=10$ となります。なので、\[ 2^{\frac{1}{0.3010} }=10 \]が成り立ちます。
解答
チ:1
ツ:5
参考
解答編 つづき
問題
(2) 次のようにして対数ものさしAを作る。
対数ものさしA 2以上の整数 $n$ のそれぞれに対して、1の目盛りから右に $\log_{10}n$ だけ離れた場所に $n$ の目盛りを書く。

(i) 対数ものさしAにおいて、3の目盛りと4の目盛りの間隔は、1の目盛りと2の目盛りの間隔 $\myBox{テ}$ 。 $\myBox{テ}$ に当てはまるものを、次の 0 ~ 2 のうちから一つ選べ。
0: より大きい
1: に等しい
2: より小さい
解説
1の目盛りを基準にすると、2の目盛りは $\log_{10}2$ だけ離れていて、3の目盛りは $\log_{10}3$ 、 4の目盛りは $\log_{10}4$ だけ離れています。
このことから、3の目盛りと4の目盛りの間隔は $\log_{10}4-\log_{10}3$ と表すことができます。これは $\log_{10}\dfrac{4}{3}$ と変形することができます。また、1の目盛りと2の目盛りの間隔は $\log_{10}2$ であり、底が1よりも大きいことから\[ \log_{10}\dfrac{4}{3}\lt \log_{10}2 \]が成り立ちます。なので、選択肢 2 が入ることがわかります。
解答
テ:2
解答編 つづき
問題
また、次のようにして対数ものさしBを作る。
対数ものさしB 2以上の整数 $n$ のそれぞれに対して、1の目盛りから左に $\log_{10}n$ だけ離れた場所に $n$ の目盛りを書く。

(ii) 次の図にように、対数ものさしAの2の目盛りと対数ものさしBの1の目盛りを合わせた。このとき、対数ものさしBの $b$ の目盛りに対応する対数ものさしAの目盛りは $a$ になった。
$a$ と $b$ の関係について、いつでも成り立つ式を、次の 0 ~ 3 のうちから一つ選べ。 $\myBox{ト}$
0: $a=b+2$
1: $a=2b$
2: $a=\log_{10}(b+2)$
3: $a=\log_{10}2b$
解説
対数ものさしAの目盛り2 と目盛り $a$ との間隔は $\log_{10}a-\log_{10}2$ です。また、対数ものさしBの目盛り1 と目盛り $b$ との間隔は $\log_{10}b$ です。これが等しいことから
\begin{eqnarray}
\log_{10}a-\log_{10}2 &=& \log_{10}b \\[5pt]
\log_{10}\frac{a}{2} &=& \log_{10}b \\[5pt]
\frac{a}{2} &=& b \\[5pt]
a &=& 2b \\[5pt]
\end{eqnarray}が成り立ちます。
解答
ト:1
解答編 つづき
問題
さらに、次のようにしてものさしCを作る。
ものさしC 自然数 $n$ のそれぞれに対して、 0 の目盛りから左に $n\log_{10}2$ だけ離れた場所に $n$ の目盛りを書く。

(iii) 次の図のように対数ものさしAの1の目盛りとものさしCの 0 の目盛りを合わせた。このとき、ものさしCの $c$ の目盛りに対応する対数ものさしAの目盛りは $d$ になった。
$c$ と $d$ の関係について、いつでも成り立つ式を、次の 0 ~ 3 のうちから一つ選べ。 $\myBox{ナ}$
0: $d=2c$
1: $d=c^2$
2: $d=2^c$
3: $c=\log_{10}d$
解説
対数ものさしAの目盛り1 と目盛り $d$ との間隔は $\log_{10}d$ です。また、ものさしCの目盛り0 と目盛り $c$ との間隔は $c\log_{10}2$ です。これが等しいことから
\begin{eqnarray}
\log_{10}d &=& c\log_{10}2 \\[5pt]
\log_{10}d &=& \log_{10}2^c \\[5pt]
d &=& 2^c \\[5pt]
\end{eqnarray}が成り立ちます。
解答
ナ:2
解答編 つづき
問題
(iv) 対数ものさしAと対数ものさしBの目盛りを一度だけ合わせるか、対数ものさしAとものさしCの目盛りを一度だけ合わせることにする。このとき、適切な箇所の目盛りを読み取るだけで実行できるものを、次の 0 ~ 5 のうちからすべて選べ。 $\myBox{ニ}$
0: $17$ に $9$ を足すこと。
1: $23$ から $15$ を引くこと。
2: $13$ に $4$ をかけること。
3: $63$ を $9$ で割ること。
4: $2$ を $4$ 乗すること。
5: $\log_2 64$ の値を求めること。
解説
対数ものさしAの目盛り $a_1,a_2$ と対数ものさしBの目盛り $b_1,b_2$ が合ったとします( $a_1\lt a_2$, $b_1\lt b_2$ )。このとき、 $\log_{10}a_2-\log_{10}a_1$ と $\log_{10}b_2-\log_{10}b_1$ が等しいということなので
\begin{eqnarray}
\log_{10}a_2-\log_{10}a_1 &=& \log_{10}b_2-\log_{10}b_1 \\[5pt]
\log_{10}\frac{a_2}{a_1} &=& \log_{10}\frac{b_2}{b_1} \\[5pt]
\frac{a_2}{a_1} &=& \frac{b_2}{b_1} \\[5pt]
\end{eqnarray}が成り立ちます。ここで、 $a_1=4$, $b_2=13$, $b_1=1$ とすると $a_2=13\times 4$ となります。つまり、対数ものさしAの目盛り4 と対数ものさしBの目盛り1 を合わせたとき、対数ものさしBの目盛り13 に対応する対数ものさしAの目盛りを見れば、そこが $13\times 4$ になる、ということです。
また、 $a_1=1$, $b_2=63$, $b_1=9$ とすると $a_2=\dfrac{63}{9}$ となります。つまり、対数ものさしAの目盛り1 と対数ものさしBの目盛り9 を合わせたとき、対数ものさしBの目盛り63 に対応する対数ものさしAの目盛りを見れば、そこが $\dfrac{63}{9}$ になる、ということです。
このように、対数ものさしAと対数ものさしBを使うことで、掛け算と割り算を計算することができます。
次に、ものさしCを使う場合を考えます。対数ものさしAの目盛り $a_1,a_2$ とものさしCの目盛り $c_1,c_2$ が合ったとします( $a_1\lt a_2$, $c_1\lt c_2$ )。このとき、 $\log_{10}a_2-\log_{10}a_1$ と $c_2\log_{10}2-c_1\log_{10}2$ が等しいということなので
\begin{eqnarray}
\log_{10}a_2-\log_{10}a_1 &=& c_2\log_{10}2-c_1\log_{10}2 \\[5pt]
\log_{10}\frac{a_2}{a_1} &=& \log_{10} 2^{c_2-c_1} \\[5pt]
\frac{a_2}{a_1} &=& 2^{c_2-c_1} \\[5pt]
\end{eqnarray}が成り立ちます。ここで、 $a_1=1$, $c_2=4$, $c_1=0$ とすると $a_2=2^4$ となります。つまり、対数ものさしAの目盛り1 とものさしCの目盛り0 を合わせたとき、ものさしCの目盛り4 に対応する対数ものさしAの目盛りを見れば、そこが $2^4$ になる、ということです。
また、 $a_1=1$, $a_2=64$, $c_1=0$ とすると $64=2^{c_2}$ となります。つまり、対数ものさしAの目盛り1 とものさしCの目盛り0 を合わせたとき、対数ものさしAの目盛り64 に対応するものさしCの目盛りを見れば、そこが $\log_2 64$ になる、ということです。
このように、対数ものさしAとものさしCを使うことで、2の累乗や2を底とする対数の値を求めることができます。
なお、これらの式変形からもわかる通り、和や差を求めることはできません。
解答
ニ:2345