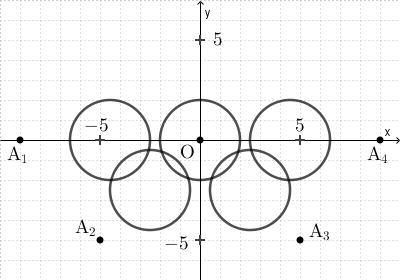共通テスト 数学II・数学B 2018年度プレテスト 第2問 [2] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
(1) 座標平面上に点 A をとる。点 P が放物線 $y=x^2$ 上を動くとき、線分 AP の中点 M の軌跡を考える。
(i) 点 A の座標が $(0,-2)$ のとき、点 M の軌跡の方程式として正しいものを、次の 0 ~ 5 のうちから一つ選べ。 $\myBox{ト}$
0: $y=x^2-1$
1: $y=2x^2-1$
2: $y=\dfrac{1}{2}x^2-1$
3: $y=|x|-1$
4: $y=2|x|-1$
5: $y=\dfrac{1}{2}|x|-1$
(ii) $p$ を実数とする。点 A の座標が $(p,-2)$ のとき、点 M の軌跡は (i) の軌跡を $x$ 軸方向に $\myBox{ナ}$ だけ平行移動したものである。 $\myBox{ナ}$ に当てはまるものを、次の 0 ~ 5 のうちから一つ選べ。
0: $\dfrac{1}{2}p$
1: $p$
2: $2p$
3: $-\dfrac{1}{2}p$
4: $-p$
5: $-2p$
(iii) $p,q$ を実数とする。点 A の座標が $(p,q)$ のとき、点 M の軌跡と放物線 $y=x^2$ との共有点について正しいものを、次の 0 ~ 5 のうちからすべて選べ。 $\myBox{ニ}$
0: $q=0$ のとき、共有点はつねに2個である。
1: $q=0$ のとき、共有点が1個になるのは $p=0$ のときだけである。
2: $q=0$ のとき、共有点は0個、1個、2個のいずれの場合もある。
3: $q\lt p^2$ のとき、共有点はつねに0個である。
4: $q=p^2$ のとき、共有点はつねに1個である。
5: $q\gt p^2$ のとき、共有点はつねに0個である。
(2) ある円 $C$ 上を動く点 Q がある。下の図は定点 $\mathrm{O}(0,0)$, $\mathrm{A}_1(-9,0)$, $\mathrm{A}_2(-5,-5)$, $\mathrm{A}_3(5,-5)$, $\mathrm{A}_4(9,0)$ に対して、線分 $\mathrm{OQ}$, $\mathrm{A_1Q}$, $\mathrm{A_2Q}$, $\mathrm{A_3Q}$, $\mathrm{A_4Q}$ のそれぞれの中点の軌跡である。このとき、円 $C$ の方程式として最も適当なものを、次の 0 ~ 7 のうちから一つ選べ。 $\myBox{ヌ}$
0: $x^2+y^2=1$
1: $x^2+y^2=2$
2: $x^2+y^2=4$
3: $x^2+y^2=16$
4: $x^2+(y+1)^2=1$
5: $x^2+(y+1)^2=2$
6: $x^2+(y+1)^2=4$
7: $x^2+(y+1)^2=16$
考え方
センター試験ではあまり出なかった軌跡の問題です。(1)の(i)(ii)は、軌跡の方程式を求めて解くのが普通ですが、選択肢から選ぶだけであれば特別な点から選択肢をしぼることもできます。ただ、(iii)は軌跡の方程式を求めないと解けないでしょう。
(2)は軌跡から逆に考える問題です。ただ、特別な点から選択肢をしぼるのがいいでしょう。円がいっぱいあって大変そうに思うかもしれませんが、実は真ん中の円について考えるだけで答えは求められます。円がいっぱいあるのは、東京オリンピックにちなんで、五輪のマークにしたかったのでしょう。
【必答問題】
解答編
問題
(1) 座標平面上に点 A をとる。点 P が放物線 $y=x^2$ 上を動くとき、線分 AP の中点 M の軌跡を考える。
(i) 点 A の座標が $(0,-2)$ のとき、点 M の軌跡の方程式として正しいものを、次の 0 ~ 5 のうちから一つ選べ。 $\myBox{ト}$
0: $y=x^2-1$
1: $y=2x^2-1$
2: $y=\dfrac{1}{2}x^2-1$
3: $y=|x|-1$
4: $y=2|x|-1$
5: $y=\dfrac{1}{2}|x|-1$
解説
点 P の座標を $(\alpha,\beta)$ とすると、 $\beta=\alpha^2$ が成り立ちます。点 M の座標を $(x,y)$ とすると\[ \dfrac{0+\alpha}{2}=x,\quad \dfrac{-2+\beta}{2}=y \]が成り立ちます。これから $\alpha=2x$, $\beta=2y+2$ が得られます。これを $\beta=\alpha^2$ に代入して
\begin{eqnarray}
2y+2 &=& (2x)^2 \\[5pt]
2y &=& 4x^2-2 \\[5pt]
y &=& 2x^2-1 \\[5pt]
\end{eqnarray}となります。これが点 M の軌跡の方程式となります。
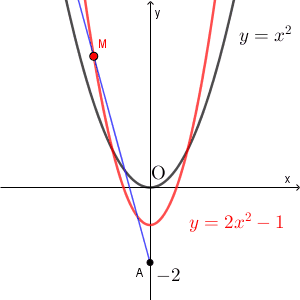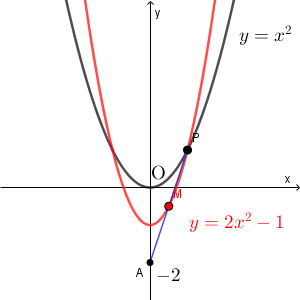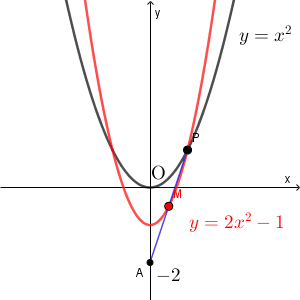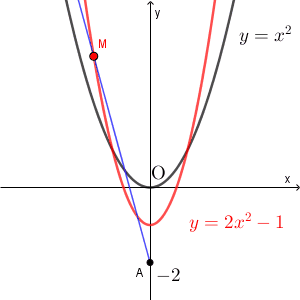
なお、選択肢から選ぶだけであれば、適当な点 P から答えをしぼっていくこともできます。例えば $(4,16)$ とすれば、このときの点 M は $(2,7)$ なので、これからも選択肢 1 にしぼることもできます。
解答
ト:1
解答編 つづき
問題
(ii) $p$ を実数とする。点 A の座標が $(p,-2)$ のとき、点 M の軌跡は (i) の軌跡を $x$ 軸方向に $\myBox{ナ}$ だけ平行移動したものである。 $\myBox{ナ}$ に当てはまるものを、次の 0 ~ 5 のうちから一つ選べ。
0: $\dfrac{1}{2}p$
1: $p$
2: $2p$
3: $-\dfrac{1}{2}p$
4: $-p$
5: $-2p$
解説
点 P の座標を $(\alpha,\beta)$ とします。点 M の座標を $(x,y)$ とすると\[ \dfrac{p+\alpha}{2}=x,\quad \dfrac{-2+\beta}{2}=y \]が成り立ちます。これから $\alpha=2x-p$, $\beta=2y+2$ が得られます。これを $\beta=\alpha^2$ に代入して
\begin{eqnarray}
2y+2 &=& (2x-p)^2 \\[5pt]
2y &=& 4\left(x-\frac{p}{2}\right)^2-2 \\[5pt]
y &=& 2\left(x-\frac{p}{2}\right)^2-1 \\[5pt]
\end{eqnarray}となります。これが点 M の軌跡の方程式となります。これは (i) の軌跡を $x$ 軸方向に $\dfrac{p}{2}$ だけ平行移動したものであることがわかります。
なお、選択肢から選ぶだけであれば、頂点に注目して答えをしぼることもできます。軌跡のうち $y$ 座標が一番小さい点は、点 P が原点にあるときに対応する M です。(i)のときはこの点が $(0,-1)$ で、今考えているケースでは $\left(\dfrac{p}{2}, -1\right)$ なので、このことからも $x$ 軸方向に $\dfrac{p}{2}$ だけ平行移動したものであることがわかります。
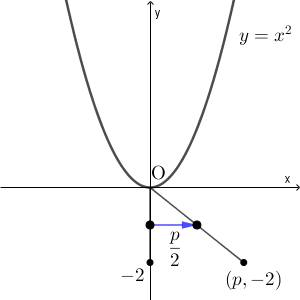
解答
ナ:0
解答編 つづき
問題
(iii) $p,q$ を実数とする。点 A の座標が $(p,q)$ のとき、点 M の軌跡と放物線 $y=x^2$ との共有点について正しいものを、次の 0 ~ 5 のうちからすべて選べ。 $\myBox{ニ}$
0: $q=0$ のとき、共有点はつねに2個である。
1: $q=0$ のとき、共有点が1個になるのは $p=0$ のときだけである。
2: $q=0$ のとき、共有点は0個、1個、2個のいずれの場合もある。
3: $q\lt p^2$ のとき、共有点はつねに0個である。
4: $q=p^2$ のとき、共有点はつねに1個である。
5: $q\gt p^2$ のとき、共有点はつねに0個である。
解説
点 P の座標を $(\alpha,\beta)$ とします。点 M の座標を $(x,y)$ とすると\[ \dfrac{p+\alpha}{2}=x,\quad \dfrac{q+\beta}{2}=y \]が成り立ちます。これから $\alpha=2x-p$, $\beta=2y-q$ が得られます。これを $\beta=\alpha^2$ に代入して
\begin{eqnarray}
2y-q &=& (2x-p)^2 \\[5pt]
2y &=& 4\left(x-\frac{p}{2}\right)^2+q \\[5pt]
y &=& 2\left(x-\frac{p}{2}\right)^2+\frac{q}{2} \\[5pt]
\end{eqnarray}となります。これが点 M の軌跡の方程式となります。
選択肢 0 ~ 2 は、 $q=0$ の場合を考えています。このときの軌跡は $y = 2\left(x-\frac{p}{2}\right)^2$ です。これと $y=x^2$ との共有点を考えます。
\begin{eqnarray}
2\left(x-\frac{p}{2}\right)^2 &=& x^2 \\[5pt]
\left(x-\frac{p}{2}\right)^2-\frac{1}{2}x^2 &=& 0 \\[5pt]
\left(x-\frac{p}{2}+\frac{\sqrt{2} }{2}x\right)\left(x-\frac{p}{2}-\frac{\sqrt{2} }{2}x\right) &=& 0 \\[5pt]
\left(\frac{1+\sqrt{2} }{2}x-\frac{p}{2}\right)\left(\frac{1-\sqrt{2} }{2}x-\frac{p}{2}\right) &=& 0 \\[5pt]
\end{eqnarray}より、 $x=\dfrac{p}{1+\sqrt{2} }$, $\dfrac{p}{1-\sqrt{2} }$ となります。これは $p=0$ のときはともに $0$ となり、 $p\ne 0$ のときは異なる値になります。このことから、共有点が1個になるのは $p=0$ のときだけで、他のケースでは共有点が2個なので、選択肢 0 ~ 2 の中では 1 が正しいとわかります。
次に選択肢 3 ~ 5 について考えます。M の軌跡 $y = 2\left(x-\frac{p}{2}\right)^2+\frac{q}{2}$ と $y=x^2$ との共有点を考えます。
\begin{eqnarray}
2\left(x-\frac{p}{2}\right)^2+\frac{q}{2} &=& x^2 \\[5pt]
2x^2-2px+\frac{p^2}{2}+\frac{q}{2} &=& x^2 \\[5pt]
x^2-2px+\frac{p^2+q}{2} &=& 0 \\[5pt]
\end{eqnarray}この実数解の個数が共有点の個数に一致します。この判別式を $D$ とすると
\begin{eqnarray}
D &=&
(-2p)^2-4 \cdot \frac{p^2+q}{2} \\[5pt]
&=&
4p^2-2p^2-2q \\[5pt]
&=& 2(p^2-q) \\[5pt]
\end{eqnarray}となります。
$q\lt p^2$ のとき、 $D\gt 0$ なので、共有点はつねに2個です。 $q=p^2$ のとき $D=0$ なので、共有点はつねに1個です。 $q\gt p^2$ のときは $D\lt 0$ なので、共有点はつねに0個です。以上から、選択肢のなかで 4, 5 が正しいことがわかります。
解答
ニ:1, 4, 5
解答編 つづき
問題
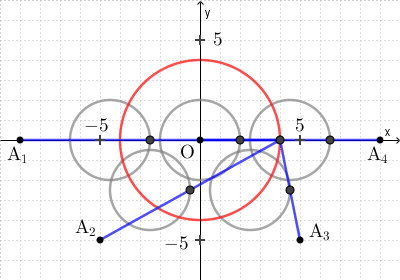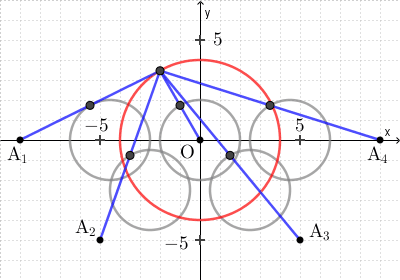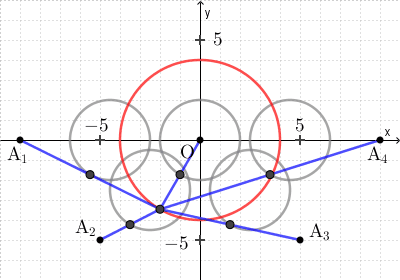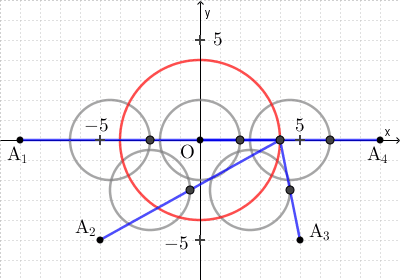
(2) ある円 $C$ 上を動く点 Q がある。下の図は定点 $\mathrm{O}(0,0)$, $\mathrm{A}_1(-9,0)$, $\mathrm{A}_2(-5,-5)$, $\mathrm{A}_3(5,-5)$, $\mathrm{A}_4(9,0)$ に対して、線分 $\mathrm{OQ}$, $\mathrm{A_1Q}$, $\mathrm{A_2Q}$, $\mathrm{A_3Q}$, $\mathrm{A_4Q}$ のそれぞれの中点の軌跡である。このとき、円 $C$ の方程式として最も適当なものを、次の 0 ~ 7 のうちから一つ選べ。 $\myBox{ヌ}$
0: $x^2+y^2=1$
1: $x^2+y^2=2$
2: $x^2+y^2=4$
3: $x^2+y^2=16$
4: $x^2+(y+1)^2=1$
5: $x^2+(y+1)^2=2$
6: $x^2+(y+1)^2=4$
7: $x^2+(y+1)^2=16$
解説
円がたくさんありますが、一つに注目して考えます。
中心が原点で半径が $2$ の円について考えます。点 Q と点 O の中点が $(0,2)$ になることから、点 Q は $(0,4)$ を通ることがわかります。選択肢の中でこの点を通るのは、選択肢 3 しかありません。
このとき、次のように、各中点の軌跡がもとの図の5つの円となります。
なお、図からわかりにくいですが、 $(1,-1)$ や $(4,-4)$ は通っていない点に注意しましょう。
解答
ヌ:3