共通テスト 数学II・数学B 2018年度プレテスト 第2問 [1] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
100g ずつ袋詰めされている食品AとBがある。1袋あたりのエネルギーは食品Aが 200kcal、食品Bが 300kcal であり、1袋あたりの脂質の含有量は食品Aが 4g、食品Bが 2g である。
(1) 太郎さんは、食品AとBを食べるにあたり、エネルギーは 1500kcal 以下に、脂質は 16g 以下に抑えたいと考えている。食べる量(g)の合計が最も多くなるのは、食品AとBをどのような量の組合せで食べるときかを調べよう。ただし、一方のみを食べる場合も含めて考えるものとする。
(i) 食品Aを $x$ 袋分、食品Bを $y$ 袋分だけ食べるとする。このとき、 $x,y$ は次の条件①, ②を満たす必要がある。
摂取するエネルギー量についての条件 $\myBox{ア}$ …①
摂取する脂質の量についての条件 $\myBox{イ}$ …②
$\myBox{ア}$, $\myBox{イ}$ に当てはまる式を、次の各解答群のうちから一つずつ選べ。
$\myBox{ア}$ の解答群
0: $200x+300y\leqq 1500$
1: $200x+300y\geqq 1500$
2: $300x+200y\leqq 1500$
3: $300x+200y\geqq 1500$$\myBox{イ}$ の解答群
0: $2x+4y\leqq 16$
1: $2x+4y\geqq 16$
2: $4x+2y\leqq 16$
3: $4x+2y\geqq 16$(ii) $x,y$ の値と条件①,②の関係について正しいものを、次の 0 ~ 3 のうちから二つ選べ。ただし、解答の順序は問わない。 $\myBox{ウ}$, $\myBox{エ}$
0: $(x,y)=(0,5)$ は条件①を満たさないが、条件②は満たす。
1: $(x,y)=(5,0)$ は条件①を満たすが、条件②は満たさない。
2: $(x,y)=(4,1)$ は条件①も条件②も満たさない。
3: $(x,y)=(3,2)$ は条件①と条件②をともに満たす。(iii) 条件①, ②をともに満たす $(x,y)$ について、食品AとBを食べる量の合計の最大値を二つの場合で考えてみよう。
食品A、Bが1袋を小分けにして食べられるような食品のとき、すなわち $x,y$ のとり得る値が実数の場合、食べる量の合計の最大値は $\myBox{オカキ}$ g である。このときの $(x,y)$ の組は、 $(x,y)=\left(\dfrac{\myBox{ク} }{\myBox{ケ} }, \dfrac{\myBox{コ} }{\myBox{サ} }\right)$ である。
次に、食品A、Bが1袋を小分けにして食べられないような食品のとき、すなわち $x,y$ のとり得る値が整数の場合、食べる量の合計の最大値は $\myBox{シスセ}$ g である。このときの $(x,y)$ の組は $\myBox{ソ}$ 通りある。
(2) 花子さんは、食品AとBを合計 600g 以上食べて、エネルギーは 1500 kcal 以下にしたい。脂質を最も少なくできるのは、食品A、Bが1袋を小分けにして食べられない食品の場合、Aを $\myBox{タ}$ 袋、Bを $\myBox{チ}$ 袋食べるときで、そのときの脂質は $\myBox{ツテ}$ g である。
考え方
健康診断におびえる中年の悩みみたいな問題ですが、それは気にせずに考えましょう。
センター試験のときはほとんど出なかった、線形計画法の問題です。とり得る値が実数の場合は授業でもやると思いますが、整数の場合はあまりやらないかもしれません。ただ、整数の場合はとり得る値の組合せは少ないので、片っ端から試していくことができます。
【必答問題】
解答編
問題
100g ずつ袋詰めされている食品AとBがある。1袋あたりのエネルギーは食品Aが 200kcal、食品Bが 300kcal であり、1袋あたりの脂質の含有量は食品Aが 4g、食品Bが 2g である。
(1) 太郎さんは、食品AとBを食べるにあたり、エネルギーは 1500kcal 以下に、脂質は 16g 以下に抑えたいと考えている。食べる量(g)の合計が最も多くなるのは、食品AとBをどのような量の組合せで食べるときかを調べよう。ただし、一方のみを食べる場合も含めて考えるものとする。
(i) 食品Aを $x$ 袋分、食品Bを $y$ 袋分だけ食べるとする。このとき、 $x,y$ は次の条件①, ②を満たす必要がある。
摂取するエネルギー量についての条件 $\myBox{ア}$ …①
摂取する脂質の量についての条件 $\myBox{イ}$ …②
$\myBox{ア}$, $\myBox{イ}$ に当てはまる式を、次の各解答群のうちから一つずつ選べ。
$\myBox{ア}$ の解答群
0: $200x+300y\leqq 1500$
1: $200x+300y\geqq 1500$
2: $300x+200y\leqq 1500$
3: $300x+200y\geqq 1500$$\myBox{イ}$ の解答群
0: $2x+4y\leqq 16$
1: $2x+4y\geqq 16$
2: $4x+2y\leqq 16$
3: $4x+2y\geqq 16$
解説
食品Aの1袋あたりのエネルギーは 200kcal なので、 $x$ 袋食べれば $200x$ kcal です。食品Bの1袋あたりのエネルギーは 300kcal なので、 $y$ 袋食べれば $300y$ kcal です。この合計を 1500kcal 以下にしたいので、エネルギー量についての条件は\[ 200x+300y\leqq 1500 \]となります。
脂質についても同様に考えると、食品Aを $x$ 袋食べれは $4x$ g、食品Bを $y$ 袋食べれば $2y$ g 摂取することになるので、これを 16g 以下にしたいという条件は\[ 4x+2y\leqq 16 \]と表すことができます。
解答
ア:0
イ:2
解答編 つづき
問題
(ii) $x,y$ の値と条件①,②の関係について正しいものを、次の 0 ~ 3 のうちから二つ選べ。ただし、解答の順序は問わない。 $\myBox{ウ}$, $\myBox{エ}$
0: $(x,y)=(0,5)$ は条件①を満たさないが、条件②は満たす。
1: $(x,y)=(5,0)$ は条件①を満たすが、条件②は満たさない。
2: $(x,y)=(4,1)$ は条件①も条件②も満たさない。
3: $(x,y)=(3,2)$ は条件①と条件②をともに満たす。
解説
それぞれの値を代入してみて、確認していきます。
条件①は、 $200x+300y\leqq 1500$ です。 $(x,y)$ が $(0,5)$ のときは左辺は $1500$ なので満たします。同様に考えて、 $(5,0)$ のときも満たす、 $(4,1)$ のときも満たす、 $(3,2)$ のときも満たす、ことがわかります。
条件②は、 $4x+2y\leqq 16$ です。 $(x,y)$ が $(0,5)$ のときは左辺は $10$ なので満たします。同様に考えて、 $(5,0)$ のときは満たさない(左辺が $20$ だから)、 $(4,1)$ のときは満たさない(左辺は $18$ だから)、 $(3,2)$ のときは満たす、ことがわかります。
以上の結果にあっている選択肢は、1 と 3 です。
解答
ウエ:1・3
解答編 つづき
問題
(iii) 条件①, ②をともに満たす $(x,y)$ について、食品AとBを食べる量の合計の最大値を二つの場合で考えてみよう。
食品A、Bが1袋を小分けにして食べられるような食品のとき、すなわち $x,y$ のとり得る値が実数の場合、食べる量の合計の最大値は $\myBox{オカキ}$ g である。このときの $(x,y)$ の組は、 $(x,y)=\left(\dfrac{\myBox{ク} }{\myBox{ケ} }, \dfrac{\myBox{コ} }{\myBox{サ} }\right)$ である。
解説
2つの条件 $200x+300y\leqq 1500$ と $4x+2y\leqq 16$ を満たす領域を考えます。1つ目の条件は
\begin{eqnarray}
200x+300y & \leqq & 1500 \\[5pt]
2x+3y & \leqq & 15 \\[5pt]
y & \leqq & -\dfrac{2}{3}x +5 \\[5pt]
\end{eqnarray}と変形できます。また、2つ目の条件は
\begin{eqnarray}
4x+2y & \leqq & 16 \\[5pt]
2x+y & \leqq & 8 \\[5pt]
y & \leqq & -2x+8 \\[5pt]
\end{eqnarray}と変形できます。また、 $y=-\dfrac{2}{3}x+5$ と $y=-2x+8$ の交点は
\begin{eqnarray}
-\dfrac{2}{3}x+5 &=& -2x+8 \\[5pt]
\dfrac{4}{3}x &=& 3 \\[5pt]
x &=& \dfrac{9}{4} \\[5pt]
\end{eqnarray}と $y=-2\cdot\dfrac{9}{4}+8=\dfrac{7}{2}$ から、 $\left(\dfrac{9}{4}, \dfrac{7}{2}\right)$ となることがわかります。
$x,y$ は $0$ 以上の値をとる、と考えていいので、条件をみたす $(x,y)$ の領域は下の図の色のついた部分となります(境界線を含む)。

食品AもBも、1袋100g なので、食べる量は $100x+100y$ で表すことができます。これを $100k$ とおくと、 $y=-x+k$ と変形できます。上の領域と共有点を持ち、 $k$ が大きくなる場合を考えると、傾きが $-2 \lt -1 \lt -\dfrac{2}{3}$ であることから、 $k$ が最大になるのは、次の場合であることがわかります。
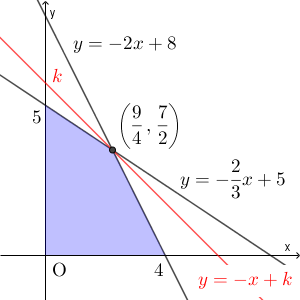
$k$ が最大になるのは $(x,y)=\left(\dfrac{9}{4}, \dfrac{7}{2}\right)$ のときであり、このとき食べる量は\[ \frac{9}{4}\times 100 + \frac{7}{2}\times 100=575 \]から、575g だとわかります。
解答
オカキ:575
クケコサ:9472
参考
解答編 つづき
問題
次に、食品A、Bが1袋を小分けにして食べられないような食品のとき、すなわち $x,y$ のとり得る値が整数の場合、食べる量の合計の最大値は $\myBox{シスセ}$ g である。このときの $(x,y)$ の組は $\myBox{ソ}$ 通りある。
解説
条件を満たす $(x,y)$ は、以下の色のついた部分(境界を含む)で、さらにどちらの座標も整数のときです。

$x$ は $0$ から $4$ までの値しかとらないので、順番に調べていくことができます。
$x\leqq 2$ の範囲では、 $y\leqq-\dfrac{2}{3}x+5$ を満たすものを考えればいいです(上のグラフから、 $x\leqq 2$ の範囲では $y=-2x+8$ の直線より $y=-\dfrac{2}{3}x+5$ のほうが下にあるため)。
$y$ が一番大きくなるときを考えればいいですね。 $x=0$ のときは $y\leqq 5$ なので、最大値は $5$ です。 $x=1$ のときは $y\leqq \frac{13}{3}$ なので、最大値は $4$ です。 $x=2$ のときは $y\leqq \frac{11}{3}$ なので、最大値は $3$ です。
$x\geqq 3$ の範囲では、 $y\leqq -2x+8$ を満たすものを考えます。 $x=3$ のときは $y$ の最大値は $2$ で、 $x=4$ のときは $y$ の最大値は $0$ です。
以上から、食べる量 $100(x+y)$ が最大になり得る候補は、 $(x,y)=$ $(0,5)$, $(1,4)$, $(2,3)$, $(3,2)$, $(4,0)$ です。これらに対し、 $100(x+y)$ を計算すると、それぞれ、 $500$, $500$, $500$, $500$, $400$ となるので、最大値は $500$ で、こうなる $(x,y)$ の組は4通りあることがわかります。
解答
シスセ:500
ソ:4
解答編 つづき
問題
(2) 花子さんは、食品AとBを合計 600g 以上食べて、エネルギーは 1500 kcal 以下にしたい。脂質を最も少なくできるのは、食品A、Bが1袋を小分けにして食べられない食品の場合、Aを $\myBox{タ}$ 袋、Bを $\myBox{チ}$ 袋食べるときで、そのときの脂質は $\myBox{ツテ}$ g である。
解説
食品Aを $x$ 袋、食品Bを $y$ 袋食べるとします。このとき、合計 600g 以上食べるという条件は\[ 100x+100y\geqq 600 \]と表すことができます。これを変形すると\[ y\geqq -x+6 \]となります。
また、エネルギーを 1500 kcal 以下にするという条件は\[ 200x+300y\leqq 1500 \]と表すことができます。これを変形すると\[ y\leqq -\frac{2}{3}x+5 \]となります。
また、 $y=-x+6$ と $y=-\dfrac{2}{3}x+5$ の交点は
\begin{eqnarray}
-x+6 &=& -\dfrac{2}{3}x+5 \\[5pt]
-\dfrac{1}{3}x &=& -1 \\[5pt]
x &=& 3 \\[5pt]
\end{eqnarray}と $y=-3+6=3$ から、 $(3,3)$ だとわかります。
$x,y$ が0以上の値をとると考えます。条件をみたす $(x,y)$ の領域は下の図の色のついた部分で、どちらの座標も整数のものです(境界線を含む)。

脂質を $k$ g とおけば、 $4x+2y=k$ が成り立ちます。これは $y=-2x+\dfrac{k}{2}$ と変形でき、2直線の傾きよりも小さいことから、 $k$ が最も小さくなるのは次のように $(3,3)$ を通るときです。
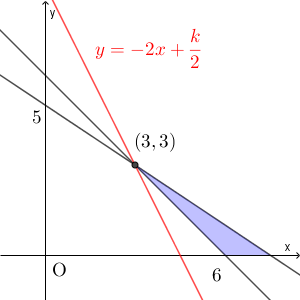
このとき、脂質は $4\cdot 3+2\cdot 3=18$ となります。
解答
タ:3
チ:3
ツテ:18





