【標準】領域と最大・最小

🕒 2017/09/21 🔄 2023/05/01

ここでは、領域を使った、最大・最小に関する問題を考えます。また、「求める領域が境界線のどちらか」を簡単に判断する方法もあわせて紹介します。

📘 目次

求める領域が境界線のどちらか、を簡単に判断する方法

例題

x, y が次の3つの不等式を満たしているとする。\[ y \leqq x,\ x-2y\leqq 1, \ 2x-y\leqq 2 \]このとき、 $x+4y$ の最大値と最小値を求めなさい。

3つの条件を組み合わせて $x+4y$ に関する条件を作り出すのは大変です。こうした問題では、まず、条件を満たす $(x,y)$ がどういう点かを考え、次に $x+4y$ の値の取りうる範囲を考える、という順番で求めていきます。

まずは、境界線の交点を求めていきましょう。それぞれ、連立方程式を解いていけばいいですね。 $y=x$ と $x-2y=1$ の交点は、 $(-1,-1)$ となります。 $x-2y=1$ と $2x-y=2$ の交点は、 $(1,0)$ です。 $2x-y=2$ と $y=x$ の交点は、 $(2,2)$ となります。

これらから、3つの不等式が表す領域は、下の色のついた部分（境界線上の点を含む）となります。

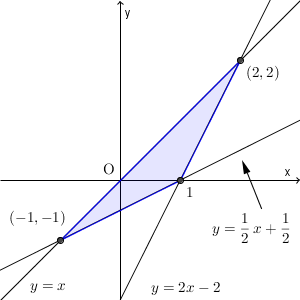
ところで、「境界線はわかるけど、どちらが考えている領域かすぐにはわからない」という人がいるかもしれません。例えば、 $2x-y\leqq 2$ の境界線は $y=2x-2$ であることはわかるが、この左上部分か、右下部分か、どちらかがすぐにわからない、ということです。

きちんと不等式を変形をして\[ y\geqq 2x-2 \]としてから考えれば、境界線よりも上の部分であることがわかります。しかし、不等号の向きは計算間違いしやすいので、検算方法があると便利ですね。実は簡単にチェックできます。

まず、原点が $2x-y\leqq 2$ を満たすか考えましょう。 $0\leqq 2$ は成り立ちます。よって、 $2x-y\leqq 2$ の表す領域に原点が含まれる、ということがわかります。そのため、境界線 $y=2x-2$ から見て原点を含む側が、不等式を表す領域だ、ということがわかります。

境界線が原点を通っていない場合には、この検算方法が使えます。同じように考えれば、 $x-2y\leqq 1$ の表す領域も原点を含むことがわかりますね。

境界線が原点を通っている場合、例えば、 $y \leqq x$ などの場合は、 x 軸上の点や y 軸上の適当な点でチェックすれば楽です。 $(0,1)$ で考えてみると、 $1\leqq 0$ という成り立たない式が出てくるので、$(0,1)$ は領域に含まれないんだな、ということがわかります。なので、この点を含んでないほうが、不等式の表す領域となります。

領域と最大・最小

さて、求める領域が分かったので、これを踏まえて $x+4y$ の値について考えていきましょう。

領域を見た感じでは、 x, y が大きければ $x+4y$ も大きくなり、 x, y が小さければ $x+4y$ も小さくなるので、 $(2,2)$ で最大、 $(-1,-1)$ で最小となるんだろう、と予想できます。

ただ、こうした考えでは、 $x-4y$ などとなった場合に困ります。領域の形や、求める式の形が変わっても使える方法を知っておいた方がいいですよね。

x, y 両方動くので考えづらいです。なので、 $x+4y=k$ とおいて、 k が取りうる範囲を考える、というように視点を切り替えます。

$x+4y=k$ を変形すると、 $y=-\dfrac{1}{4}x+\dfrac{1}{4}k$ となります。このことから、次のように考えることができます。

この領域内の点に対し、その点を通る傾き $-\dfrac{1}{4}$ の直線をひきます。このとき、切片が $\dfrac{1}{4}k$ になる、つまり、切片を $4$ 倍したものが、その点に対応する $x+4y$ の値だ、ということです。

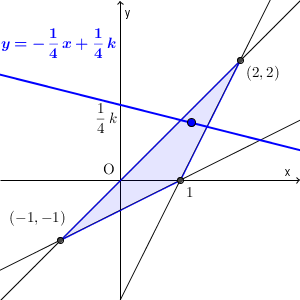
このことから、この領域と共有点を持つように、傾き $-\dfrac{1}{4}$ の直線を動かし、y 軸との交点が一番上の場合が最大、一番下の場合が最小になる、ということがわかります。

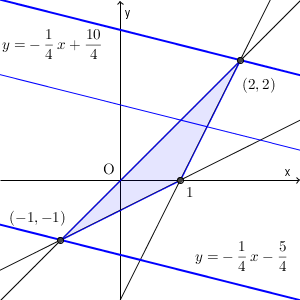
そのため、図より、 $y=-\dfrac{1}{4}x+\dfrac{1}{4}k$ の切片が最大になるときは $(2,2)$ と通るとき、最小になるのは $(-1,-1)$ を通るときであることがわかります。

よって、 $x+4y$ が最大になるのは、 $x=2,y=2$ のときで、その値は $10$ です。最小になるのは、 $x=-1,y=-1$ のときで、その値は $-5$ です。これが答えです。

これが、もし「 $2x-3y$ の最大・最小を求めなさい」だったら、 $2x-3y=k$ とおき、 $y=\dfrac{2}{3}x-\dfrac{1}{3}k$ と変形し、この直線と領域とが共有点を持つように動かすことになります。

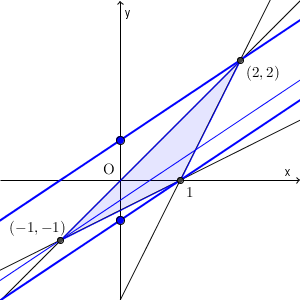
最大・最小をとる点がかわることや k の符号に注意しましょう。この場合、 $2x-3y$ が最大になるのは、切片が一番小さくなるときであり、 $x=1,y=0$ のときで、その値は $2$ です。最小は、切片が一番大きくなるときであり、 $x=2,y=2$ のときで、その値は $-2$ となります。

「式の値が最大だから切片も最大」とはならないことに注意しましょう。また、式の形によって、最大・最小をとる点が変わることにも注意しましょう。これらのことから、きちんと図をかいて解答するようにしましょう。