【基本】極大値と極小値

🕒 2017/10/18 🔄 2023/05/01

ここでは、極大値と極小値についてみていきます。なお、ここで出てくる関数は、整式で表されるものを想定しています。

（2020年8月10日追記：極値の定義を、微分可能性を仮定しないものに書き換え、全体的に記事を書き直しました。）

📘 目次

極大値と極小値

【基本】増減表では、増減表の書き方、そして、それを利用したグラフのかき方をみました。導関数の符号を調べることで、関数が単調に増加しているのか、単調に減少しているのかがわかるのでしたね。

例えば、 $f(x)=2x^3-x$ という関数であれば、 $f'(x)=6x^2-1$ であることから、増減表は次のようになります。
\begin{array}{c|ccccc} x & \cdots & -\frac{\sqrt{6} }{6} & \cdots & \frac{\sqrt{6} }{6} & \cdots \\ \hline f’(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & \frac{\sqrt{6} }{9} & \searrow & -\frac{\sqrt{6} }{9} & \nearrow \end{array}これより、 $y=f(x)$ のグラフは、次のようになることがわかります。

増減表を見れば、 $x=-\dfrac{\sqrt{6} }{6}$ の前後で、導関数の符号がプラスからマイナスになることや、 $x=\dfrac{\sqrt{6} }{6}$ の前後で、導関数の符号がマイナスからプラスになることがわかります。その結果、山や谷ができることがわかるのですね。

この山の頂上の部分 $(x=-\frac{\sqrt{6} }{6}$ のところ $)$ はグラフの特徴的な点です。定義域全体で見ると最大ではないですが、この点のまわりでは最大です。このような、局所的な最大値のことを極大値といいます。

一方、谷底の部分にも名前がついています。ここも、定義域全体で見ると最小ではないですが、この点のまわりでは最小です。このような、局所的な最小値のことを極小値といいます。

また、極大値と極小値をまとめて極値といいます。

式を使って書くと、次のようになります。

極大値・極小値

$x=a$ を含む小さい区間で、 $x\ne a$ ならば $f(x)\lt f(a)$ が成り立つとき、 $f(x)$ は $x=a$ で極大になる、といい、 $f(a)$ のことを極大値という。
$x=a$ を含む小さい区間で、 $x\ne a$ ならば $f(x)\gt f(a)$ が成り立つとき、 $f(x)$ は $x=a$ で極小になる、といい、 $f(a)$ のことを極小値という。
極大値と極小値をまとめて極値という。

例えば、「極値を求めなさい」といわれたら、極大値と極小値の両方を求める、ということです。

$f(x)$ が微分可能な場合（数学IIでは基本的に微分可能な場合しか出てきませんが）、上の増減表からもわかる通り、 $x=a$ の前後で導関数の符号がプラスからマイナスへと切り替わるとき、関数の値は増加から減少に切り替わり、グラフは山のような形となるため、 $x=a$ で極大値をとることになります。

逆に、 $x=a$ の前後で導関数の符号がマイナスからプラスへと切り替わるとき、関数の値は減少から増加に切り替わり、グラフは谷のような形となるため、 $x=a$ で極小値をとることになります。

極値をとるところでは、導関数の符号がプラスからマイナスになるか、マイナスからプラスになります。どちらの場合であっても、極値をとるところでは、導関数の値は $0$ となることがわかります。

極大値・極小値

$f(x)$ が微分できる場合は、以下のことが成り立つ。
$x=a$ の前後で $f'(x)$ の符号が正から負に変わるとき、 $f(a)$ は極大値となる。
$x=a$ の前後で $f'(x)$ の符号が負から正に変わるとき、 $f(a)$ は極小値となる。
$f(x)$ が $x=a$ で極値をとるなら、 $f'(a)=0$ となる。

極大値と極小値に関する注意

極大値・極小値について、少し注意が必要なところがあります。

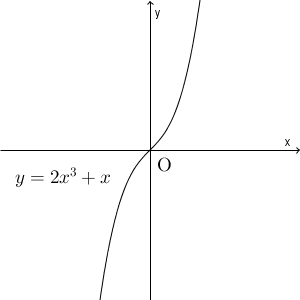
1つは、「必ずしも極値が存在するわけではない」ということです。例えば、 $y=2x^3+x$ という関数を考えてみましょう。この場合 $y'=6x^2+1$ なので、導関数は常に正です。なので、「正から負」になる部分も「負から正」になる部分もありません。よって、この場合、極値は存在しません。常に単調に増加することがわかります。

また、「 $x=a$ で極値をとるなら $f'(a)=0$ 」と書きましたが、逆は成り立ちません。つまり、 $f'(a)=0$ でも、 $x=a$ で極値をとるとは限らないんですね。例えば、 $y=x^3$ という関数であれば、導関数は $y'=3x^2$ です。よって $f'(0)=0$ となります。しかし、この前後の導関数の符号を見ると、「正から正」です。そのため、山や谷にはなりません。

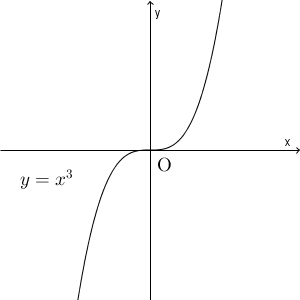
この場合も、極値はとりません。

つまり、 $f'(x)=0$ を満たす x は、極値をとる候補ではありますが、極値をとるとはいえないんですね。そのため、こうした候補を計算してから、1つ1つ、この値の前後で導関数の符号がどうなっているかを調べる必要があります。正から負、負から正のどちらかとなっている場合でなければ、極値をとるとは限りません。

以後、こうしたことに注意していきましょう。