センター試験数学I・数学A 2020年度第1問 [3] 解説

🕒 2020/01/19 🔄 2023/05/01

【必答問題】

問題編

問題

　$c$ を定数とする。2次関数 $y=x^2$ のグラフを、2点 $(c,0)$, $(c+4, 0)$ を通るように平行移動して得られるグラフを $G$ とする。

(1) $G$ をグラフに持つ2次関数は、 $c$ を用いて\[ y=x^2-2\left(c+\myBox{ツ}\right)x+c\left(c+\myBox{テ}\right) \]と表せる。

　2点 $(3,0)$, $(3,-3)$ を両端とする線分と $G$ が共有点をもつような $c$ の値の範囲は\[ -\myBox{ト}\leqq c\leqq \myBox{ナ},\ \myBox{ニ}\leqq c\leqq \myBox{ヌ} \]である。

(2) $\mybox{ニ}\leqq c\leqq \mybox{ヌ}$ の場合を考える。 $G$ が点 $(3,-1)$ を通るとき、 $G$ は2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\myBox{ネ}+\sqrt{\myBox{ノ} }$ 、 $y$ 軸方向に $\myBox{ハヒ}$ だけ平行移動したものである。また、このとき $G$ と $y$ 軸との交点の $y$ 座標は $\myBox{フ}+\myBox{ヘ}\sqrt{\myBox{ホ} }$ である。

考え方

(1)の後半は、グラフをかいて見ると、どういう不等式を求めればいいかがわかりやすくなります。

(2)は、特徴的な点に着目して、どのように移動しているかを考えましょう。なお、後半は前半ができなくてもできます。

【必答問題】

解答編

問題

　$c$ を定数とする。2次関数 $y=x^2$ のグラフを、2点 $(c,0)$, $(c+4, 0)$ を通るように平行移動して得られるグラフを $G$ とする。

(1) $G$ をグラフに持つ2次関数は、 $c$ を用いて\[ y=x^2-2\left(c+\myBox{ツ}\right)x+c\left(c+\myBox{テ}\right) \]と表せる。

解説

$G$ は $y=x^2$ のグラフを平行移動したものなので、 $G$ をグラフに持つ2次関数の $x^2$ の係数は $1$ です。また、グラフ $G$ が通る2点 $(c,0)$, $(c+4, 0)$ は $x$ 軸上の点なので、 $G$ をグラフに持つ2次関数は、
\begin{eqnarray} y &=& (x-c)\{x-(c+4)\} \\[5pt] &=& x^2+(-2c-4)x+c(c+4) \\[5pt] &=& x^2-2(c+2)x+c(c+4) \\[5pt] \end{eqnarray}と求められます。

解答

ツテ：24

解答編つづき

問題

　2点 $(3,0)$, $(3,-3)$ を両端とする線分と $G$ が共有点をもつような $c$ の値の範囲は\[ -\myBox{ト}\leqq c\leqq \myBox{ナ},\ \myBox{ニ}\leqq c\leqq \myBox{ヌ} \]である。

解説

グラフが次のようになっているケースを考えます。

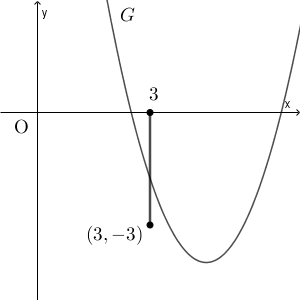
2点 $(3,0)$, $(3,-3)$ を両端とする線分と $G$ が共有点をもつのは、 $x=3$ のときの $y$ 座標が $-3$ 以上 $0$ 以下となる場合です。
\begin{eqnarray} & & 3^2-2(c+2)\cdot 3+c(c+4) \\[5pt] &=& 9-6c-12+c^2+4c \\[5pt] &=& c^2-2c-3 \\[5pt] \end{eqnarray}なので、これが $-3$ 以上 $0$ 以下となる範囲を求めます。

$c^2-2c-3\leqq 0$ は $(c-3)(c+1)\leqq 0$ なので、 $-1\leqq c\leqq 3$ です。

$c^2-2c-3\geqq -3$ は $c(c-2)\geqq 0$ なので、 $c\geqq 2$ または $c\leqq 0$ です。

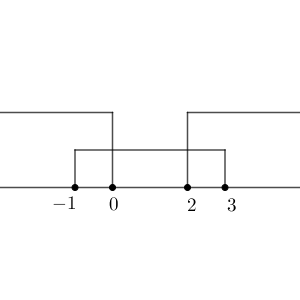
この両方の範囲に含まれているものが答えなので、 $-1\leqq c \leqq 0$ または $2\leqq c \leqq 3$ となります。

解答

トナニヌ：1023

解答編つづき

問題

(2) $\mybox{ニ}\leqq c\leqq \mybox{ヌ}$ の場合を考える。 $G$ が点 $(3,-1)$ を通るとき、 $G$ は2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\myBox{ネ}+\sqrt{\myBox{ノ} }$ 、 $y$ 軸方向に $\myBox{ハヒ}$ だけ平行移動したものである。

解説

まず、グラフの平行移動について考えるために、 $G$ の頂点の座標を考えます。
\begin{eqnarray} y &=& x^2-2(c+2)x+c(c+4) \\[5pt] &=& \{x-(c+2)\}^2-(c+2)^2+c(c+4) \\[5pt] &=& \{x-(c+2)\}^2-c^2-4c-4+c^2+4c \\[5pt] &=& \{x-(c+2)\}^2-4 \\[5pt] \end{eqnarray}なので、頂点の座標は $(c+2, -4)$ となります。よって、グラフ $G$ は $y=x^2$ のグラフを $x$ 軸方向に $c+2$ 移動し、 $y$ 軸方向に $-4$ 移動したものであることがわかります。

次に、 $c$ の値を求めます。グラフ $G$ は $(3,-1)$ を通るので、
\begin{eqnarray} c^2-2c-3 &=& -1 \\[5pt] c^2-2c-2 &=& 0 \\[5pt] c &=& 1\pm\sqrt{3} \end{eqnarray}となりますが、今考えている範囲は $2\leqq c \leqq 3$ なので、 $c=1+\sqrt{3}$ です。

以上から、グラフ $G$ の頂点は $(c+2,-4)=(3+\sqrt{3},-4)$ なので、 $G$ は $y=x^2$ のグラフを $x$ 軸方向に $3+\sqrt{3}$ 移動し、 $y$ 軸方向に $-4$ 移動したものであることがわかります。

なお、前半部分は、次のように考えることもできます。 $y=x^2$ のグラフ上の点で、 $y$ 座標が同じで $x$ 座標の差が $4$ となる点は $(-2,4)$, $(2,4)$ です。なので、 $(-2,4)$ が $(c,0)$ に平行移動したと考えれば、 $x$ 軸方向に $c+2$ 移動し、 $y$ 軸方向に $-4$ 移動したものであることがわかります。

解答

ネノハヒ：33-4

解答編つづき

問題

また、このとき $G$ と $y$ 軸との交点の $y$ 座標は $\myBox{フ}+\myBox{ヘ}\sqrt{\myBox{ホ} }$ である。

解説

ツテより、グラフ $G$ と $y$ 軸との交点の $y$ 座標は $c(c+4)$ なので、
\begin{eqnarray} c(c+4) &=& (1+\sqrt{3})(5+\sqrt{3}) \\[5pt] &=& 8+6\sqrt{3} \\[5pt] \end{eqnarray}となります。