センター試験 数学I・数学A 2020年度 第5問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
$\triangle \mathrm{ABC}$ において、辺 $\mathrm{BC}$ を $7:1$ に内分する点を $\mathrm{D}$ とし、辺 $\mathrm{AC}$ を $7:1$ に内分する点を $\mathrm{E}$ とする。線分 $\mathrm{AD}$ と線分 $\mathrm{BE}$ の交点を $\mathrm{F}$ とし、直線 $\mathrm{CF}$ と辺 $\mathrm{AB}$ の交点を $\mathrm{G}$ とすると
$\dfrac{\mathrm{GB} }{\mathrm{AG} }=\myBox{ア}$, $\dfrac{\mathrm{FD} }{\mathrm{AF} }=\dfrac{\myBox{イ} }{\myBox{ウ} }$, $\dfrac{\mathrm{FC} }{\mathrm{GF} }=\dfrac{\myBox{エ} }{\myBox{オ} }$
である。したがって\[ \dfrac{\triangle\mathrm{CDG}\sf{の面積}}{\triangle\mathrm{BFG}\sf{の面積}}=\dfrac{\myBox{カ} }{\myBox{キク} } \]となる。
4点 $\mathrm{B, D, F, G}$ が同一円周上にあり、かつ $\mathrm{FD}=1$ のとき\[ \mathrm{AB}=\myBox{ケコ} \]である。さらに $\mathrm{AE}=3\sqrt{7}$ とするとき、 $\mathrm{AE\cdot AC}=\myBox{サシ}$ であり\[ \angle\mathrm{AEG}=\myBox{ス} \]である。 $\mybox{ス}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
0: $\angle\mathrm{BGE}$
1: $\angle\mathrm{ADB}$2: $\angle\mathrm{ABC}$
3: $\angle\mathrm{BAD}$
考え方
見るからに、チェバやメネラウスの定理を使う雰囲気があります。視点を変えて、適用していきます。面積比は辺の比を利用すれば求められます。
後半は、4点が同一円周上にあることから、何を使うかピンとくるでしょう。最後の角度の問題は、そこまでで円が登場しているので、何を使うのか予測しやすいでしょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
$\triangle \mathrm{ABC}$ において、辺 $\mathrm{BC}$ を $7:1$ に内分する点を $\mathrm{D}$ とし、辺 $\mathrm{AC}$ を $7:1$ に内分する点を $\mathrm{E}$ とする。線分 $\mathrm{AD}$ と線分 $\mathrm{BE}$ の交点を $\mathrm{F}$ とし、直線 $\mathrm{CF}$ と辺 $\mathrm{AB}$ の交点を $\mathrm{G}$ とすると
$\dfrac{\mathrm{GB} }{\mathrm{AG} }=\myBox{ア}$, $\dfrac{\mathrm{FD} }{\mathrm{AF} }=\dfrac{\myBox{イ} }{\myBox{ウ} }$, $\dfrac{\mathrm{FC} }{\mathrm{GF} }=\dfrac{\myBox{エ} }{\myBox{オ} }$
である。
解説
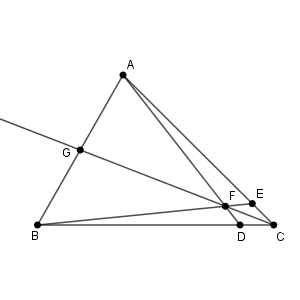
チェバの定理より
\begin{eqnarray}
\frac{\mathrm{GB} }{\mathrm{AG} } \cdot \frac{\mathrm{DC} }{\mathrm{BD} } \cdot \frac{\mathrm{EA} }{\mathrm{CE} } &=& 1 \\[5pt]
\frac{\mathrm{GB} }{\mathrm{AG} } \cdot \frac{1}{7} \cdot \frac{7}{1} &=& 1 \\[5pt]
\frac{\mathrm{GB} }{\mathrm{AG} } &=& 1 \\[5pt]
\end{eqnarray}となります。
次に、三角形 ABD と直線 CG に着目します。
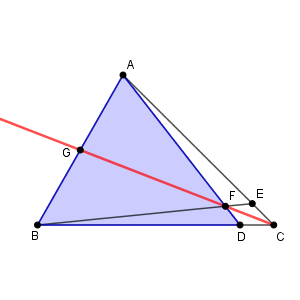
これらに対してメネラウスの定理を使うと
\begin{eqnarray}
\frac{\mathrm{CD} }{\mathrm{BC} } \cdot \frac{\mathrm{FA} }{\mathrm{DF} } \cdot \frac{\mathrm{GB} }{\mathrm{AG} } &=& 1 \\[5pt]
\frac{1}{8} \cdot \frac{\mathrm{FA} }{\mathrm{DF} } \cdot 1 &=& 1 \\[5pt]
\frac{\mathrm{FD} }{\mathrm{AF} } &=& \frac{1}{8} \\[5pt]
\end{eqnarray}となります。
最後に、三角形 BCG と直線 AD に着目します。
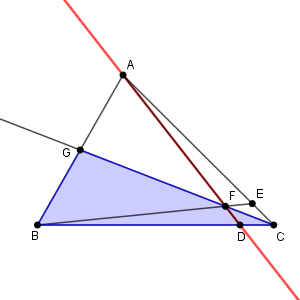
これらに対してメネラウスの定理を使うと
\begin{eqnarray}
\frac{\mathrm{DC} }{\mathrm{BD} } \cdot \frac{\mathrm{FG} }{\mathrm{CF} } \cdot \frac{\mathrm{AB} }{\mathrm{GA} } &=& 1 \\[5pt]
\frac{1}{7} \cdot \frac{\mathrm{FG} }{\mathrm{CF} } \cdot \frac{2}{1} &=& 1 \\[5pt]
\frac{\mathrm{FC} }{\mathrm{GF} } &=& \frac{2}{7} \\[5pt]
\end{eqnarray}となります。
解答
アイウエオ:11827
解答編 つづき
問題
したがって\[ \dfrac{\triangle\mathrm{CDG}\sf{の面積}}{\triangle\mathrm{BFG}\sf{の面積}}=\dfrac{\myBox{カ} }{\myBox{キク} } \]となる。
解説

$\triangle\mathrm{CDG}$ の面積は $\triangle\mathrm{BCG}$ の面積の $\dfrac{1}{8}$ 倍であり、 $\triangle\mathrm{BFG}$ の面積は $\triangle\mathrm{BCG}$ の面積の $\dfrac{\mathrm{FG} }{\mathrm{CG} }=\dfrac{7}{9}$ 倍だから、 $\triangle\mathrm{CDG}$ の面積 を $\triangle\mathrm{BFG}$ の面積で割った値は\[ \dfrac{1}{8}\div\dfrac{7}{9}=\dfrac{9}{56} \]となります。
解答
カキク:956
解答編 つづき
問題
4点 $\mathrm{B, D, F, G}$ が同一円周上にあり、かつ $\mathrm{FD}=1$ のとき\[ \mathrm{AB}=\myBox{ケコ} \]である。
解説
図は正しくないですが、先ほどの図を使いまわして考えていきます。

4点 $\mathrm{B, D, F, G}$ が同一円周上にあるとき、方べきの定理から $\mathrm{AF}\cdot \mathrm{AD}=\mathrm{AG}\cdot \mathrm{AB}$ が成り立ちます。 $\mathrm{FD}=1$ なので、 $\mathrm{AF}=8$, $\mathrm{AD}=9$ であり、 $\mathrm{AG}\cdot \mathrm{AB}=\dfrac{\mathrm{AB}^2}{2}$ だから、 $\dfrac{\mathrm{AB}^2}{2}=72$ より $\mathrm{AB}=12$ と求められます。
解答
ケコ:12
解答編 つづき
問題
さらに $\mathrm{AE}=3\sqrt{7}$ とするとき、 $\mathrm{AE\cdot AC}=\myBox{サシ}$ であり\[ \angle\mathrm{AEG}=\myBox{ス} \]である。 $\mybox{ス}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
0: $\angle\mathrm{BGE}$
1: $\angle\mathrm{ADB}$2: $\angle\mathrm{ABC}$
3: $\angle\mathrm{BAD}$
解説

$\mathrm{AE}=3\sqrt{7}$ のとき、$\mathrm{AC}=\dfrac{8}{7}\mathrm{AE}$ だから、
\begin{eqnarray}
\mathrm{AE}\cdot \mathrm{AC}
&=&
\dfrac{8}{7}\cdot \mathrm{AE}^2 \\[5pt]
&=&
\dfrac{8}{7}\cdot 9\cdot 7 \\[5pt]
&=&
72
\end{eqnarray}となります。この値は、 $\mathrm{AG}\cdot \mathrm{AB}=72$ と等しいので、方べきの定理の逆より、4点 $\mathrm{G, B, C, E}$ が同一円周上にあることがわかります。よって、 $\angle \mathrm{AEG}=\angle \mathrm{ABC}$ が成り立ちます。
解答
サシス:722





