センター試験 数学I・数学A 2019年度追試 第1問 [3] 解説
【必答問題】
問題編
問題
a と b はいずれも0でない実数とする。 x の方程式\[ bx^2+2(2a-b)x+b-4a+3=0\quad\cdots① \]を考える。
(1) 方程式①が異なる二つの実数解をもつのは\[ b\lt\dfrac{\myBox{ツ} }{\myBox{テ} }a^2 \]のときである。このとき、二つの実数解は\[ x=\dfrac{b-\myBox{ト}a\pm\sqrt{\mybox{ツ}a^2-\mybox{テ}b} }{b} \]である。
(2) $b=a^2$ とする。方程式①が異なる二つの実数解をもち、それらの一方が正の解で他方が負の解であるような a の値の範囲は\[ \myBox{ナ}\lt a \lt \myBox{ニ} \]である。また、方程式①が異なる二つの実数解をもち、それらがいずれも正の解であるような a の値の範囲は\[ a\lt\myBox{ヌ}\ ,\quad a\gt \myBox{ネ} \]である。
考え方
(1)は判別式や解の公式を使って計算をします。計算量もそれほど多くはありません。
(2)のようなタイプは、グラフを用いて考えることが多いですが、(1)で解を求めているのでこちらを使って考えても構いません。分母にも文字が入っているので、符号に気を付けて考えましょう。
【必答問題】
解答編
問題
a と b はいずれも0でない実数とする。 x の方程式\[ bx^2+2(2a-b)x+b-4a+3=0\quad\cdots① \]を考える。
(1) 方程式①が異なる二つの実数解をもつのは\[ b\lt\dfrac{\myBox{ツ} }{\myBox{テ} }a^2 \]のときである。このとき、二つの実数解は\[ x=\dfrac{b-\myBox{ト}a\pm\sqrt{\mybox{ツ}a^2-\mybox{テ}b} }{b} \]である。
解説
$b\ne 0$ なので、①は二次方程式です。これが異なる二つの実数解をもつことは、判別式が正であることと同値です。判別式を $D$ とおくと
\begin{eqnarray}
\dfrac{D}{4}
&=&
(2a-b)^2-b(b-4a+3) \\[5pt]
&=&
(4a^2-4ab+b^2)-(b^2-4ab+3b) \\[5pt]
&=&
4a^2-3b \\[5pt]
\end{eqnarray}なので、これが正であることは
\begin{eqnarray}
4a^2-3b \gt 0 \\[5pt]
b \lt \frac{4}{3}a^2 \\[5pt]
\end{eqnarray}と同値です。
このときの実数解は、解の公式より、
\begin{eqnarray}
x
&=&
\frac{-2(2a-b)\pm\sqrt{D} }{2b} \\[5pt]
&=&
\frac{b-2a\pm\sqrt{4a^2-3b} }{b} \\[5pt]
\end{eqnarray}となります。
解答
ツテ:43
ト:2
参考
解答編 つづき
(2) $b=a^2$ とする。方程式①が異なる二つの実数解をもち、それらの一方が正の解で他方が負の解であるような a の値の範囲は\[ \myBox{ナ}\lt a \lt \myBox{ニ} \]である。
解説
まず、 $b=a^2$ は、(1)の条件を満たしているので、方程式①は異なる二つの実数解をもつことに点に注意しましょう。
$b=a^2$ のときを考えるので、代入して文字を一つ減らしましょう。 $a$ に関する条件を考えるので、 $b$ へ代入します。
実数解の片方が正で片方が負の場合を考えるので、実数解を表す式に $b=a^2$ を代入します。
\begin{eqnarray}
x
&=&
\frac{a^2-2a\pm\sqrt{4a^2-3a^2} }{a^2} \\[5pt]
&=&
\frac{a^2-2a\pm\sqrt{a^2} }{a^2} \\[5pt]
\end{eqnarray}となります。 $\pm\sqrt{a^2}$ は、 $a$ が正のときも負のときも、 $a$ と $-a$ を表すので、実数解は、 $x=\dfrac{a^2-2a+a}{a^2}$, $\dfrac{a^2-2a-a}{a^2}$ となります。計算すると、 $x=\dfrac{a-1}{a}$, $\dfrac{a-3}{a}$ です。これらが、片方が正で片方が負になる場合を考えます。
まず、 $a$ が負の場合を考えます。この場合、どちらも分母は負で、分子も負です。そのため、実数解はどちらも正になってしまいます。
残りは正の場合です。この場合、どちらも分母は正なので、分子だけを考えればいいですね。 $a-1$ と $a-3$ なら、後者のほうが小さいので、\[ a-1\gt 0,\quad a-3\lt 0 \]となる場合しかありません。こうして、\[ 1\lt a\lt 3 \]のときであることがわかります。
ここでは、解から考えましたが、二次関数のグラフから考えることも可能です。①の左辺を用いて、次のような二次関数を考えます。
\begin{eqnarray}
y
&=&
bx^2+2(2a-b)x+b-4a+3 \\[5pt]
&=&
a^2x^2+2(2a-a^2)x+a^2-4a+3 \\[5pt]
\end{eqnarray}このグラフと $x$ 軸との交点の $x$ 座標が、①の方程式の解と一致します。グラフが $x$ 軸の正の部分と負の部分の両方と交わるのは、グラフが次のようになっているときです。
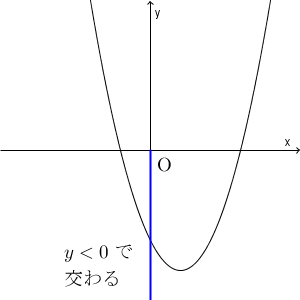
$x^2$ の係数がつねに正なので、グラフは下に凸となります。なので、 $y$ 軸と負の部分で交わっていれば、グラフは必ず $x$ 軸の正の部分と負の部分の両方と交わります。逆に、負の部分と交わっていない場合は、 $x$ 軸の正の部分と負の部分の両方に交わることはありません。
以上から、 $x=0$ としたときに負になる範囲を求めればよく
\begin{eqnarray}
a^2-4a+3 & \lt & 0 \\[5pt]
(a-1)(a-3) & \lt & 0 \\[5pt]
\end{eqnarray}から、 $1\lt a\lt 3$ と求めることもできます。
解答
ナニ:13
参考
解答編 つづき
また、方程式①が異なる二つの実数解をもち、それらがいずれも正の解であるような a の値の範囲は\[ a\lt\myBox{ヌ}\ ,\quad a\gt \myBox{ネ} \]である。
解説
これも、まずは実数解から考えてみましょう。
実数解は、 $x=\dfrac{a-1}{a}$, $\dfrac{a-3}{a}$ と表せるのでした。これらがともに正になる場合を考えます。
$a$ が負の場合は、どちらも分母は負で、分子も負です。そのため、実数解はどちらも正になります。
$a$ が正の場合は、どちらも分母は正なので、分子だけを考えればいいです。 $a-1$ と $a-3$ なら、後者のほうが小さいので、\[ a-3\gt 0 \]であればいいですね。つまり、\[ a\gt 3 \]のときです。
こうして、2つの正の解をもつ $a$ の範囲は、 $a\lt 0$, $a\gt 3$ となります。
これも、グラフを使って考えることもできます。2つの正の解をもつのは、グラフが次のようになっているときです。
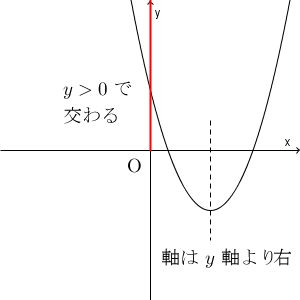
まず、先ほどの問題でも使った $y$ 軸との関係を見ると、 $y$ 軸と正の部分で交わっている、という条件を使うことがわかります。ただ、これだけでは、「ともに負」の場合もあります。そこで、放物線の軸が $y$ 軸よりも右にある、という条件も使います。これらを満たしていれば、必ず2つの正の解をもつし、これを満たしていない場合は2つの正の解をもつことはありません。
$y$ 軸と正の部分で交わることは、\[ a^2-4a+3\gt 0 \]を解いて、 $a\lt 1$, $a\gt 3$ となります。次に、放物線の軸を考えます。 $x^2$ と $x$ の項を平方完成して
\begin{eqnarray}
& &
a^2x^2+2(2a-a^2)x \\[5pt]
&=&
a^2 \left(x^2+\frac{2(2-a)}{a}x\right) \\[5pt]
&=&
a^2 \left(x+\frac{2-a}{a}\right)^2-(2-a)^2 \\[5pt]
\end{eqnarray}となることから、放物線の軸は $y=\dfrac{a-2}{a}$ となります。これが正となることは、 $a\gt 2$, $a\lt 0$ と同値です。
以上から、「 $(a\lt 1$ または $a\gt 3)$ かつ $(a\gt 2$ または $a\lt 0)$ 」をまとめて、「 $a\lt 0$ または $a\gt 3$ 」となります。
解答
ヌネ:03





