センター試験 数学I・数学A 2019年度追試 第5問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=\sqrt{6}$, $\mathrm{ BC }=4$, $\cos\angle \mathrm{ ABC }=\dfrac{\sqrt{6} }{9}$ とする。
辺 BC 上の点 D を $\mathrm{ BD }=1$ となるようにとり、 $\triangle \mathrm{ ACD }$ の外接円の辺 AB の交点で、点 A とは異なる点を E とする。このとき\[ \mathrm{ BE }\cdot \mathrm{ BA }=\myBox{ア} \]であるから、 $\mathrm{ BE }=\dfrac{\myBox{イ}\sqrt{\myBox{ウ} }}{\myBox{エ} }$ である。線分 AD と線分 EC の交点を P とすると\[ \frac{\mathrm{ AP } }{\mathrm{ PD } }=\dfrac{\myBox{オ} }{\myBox{カ} } \]である。 $\mathrm{ AD }=\dfrac{\sqrt{\myBox{キク} }}{\myBox{ケ} }$ であるから、 $\mathrm{ PD }=\dfrac{\sqrt{\myBox{コサ} }}{\myBox{シ} }$ である。また、 $\cos\angle \mathrm{ ADB }=\dfrac{\sqrt{\myBox{スセ} }}{\myBox{ソタ} }$ である。
次に、 $\triangle \mathrm{ AEP }$ の外接円と直線 BP の交点で、点 P とは異なる点を L とする。\[ \mathrm{ BP }\cdot \mathrm{ BL }=\myBox{チ} \]である。\[ \mathrm{ BD }\cdot \mathrm{ BC }=4 \]であるから、 $\tan\angle \mathrm{ BLC }=\myBox{ツ}\sqrt{\myBox{テ} }$ である。
考え方
この分野で学ぶ有名な定理を用いて解いていく問題です。ただ、三角比の内容を使うところが多いので、三角比の内容がわかっていないと詰まるところが多いです。
最後の設問は、途中で $\cos$ の値を求めたことを考えれば、どのように解けばいいか思いつきやすいでしょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=\sqrt{6}$, $\mathrm{ BC }=4$, $\cos\angle \mathrm{ ABC }=\dfrac{\sqrt{6} }{9}$ とする。
辺 BC 上の点 D を $\mathrm{ BD }=1$ となるようにとり、 $\triangle \mathrm{ ACD }$ の外接円の辺 AB の交点で、点 A とは異なる点を E とする。このとき\[ \mathrm{ BE }\cdot \mathrm{ BA }=\myBox{ア} \]であるから、 $\mathrm{ BE }=\dfrac{\myBox{イ}\sqrt{\myBox{ウ} }}{\myBox{エ} }$ である。
解説
図は次のようになっています。
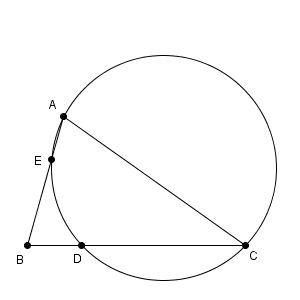
方べきの定理より\[ \mathrm{ BE }\cdot \mathrm{ BA }=\mathrm{ BD }\cdot \mathrm{ BC }=1\cdot4=4 \]と求められます。 $\mathrm{ AB }=\sqrt{6}$ なので、\[ \mathrm{ BE }=\frac{4}{\sqrt{6} }=\frac{2\sqrt{6} }{3} \]となります。
解答
ア:4
イウエ:263
解答編 つづき
線分 AD と線分 EC の交点を P とすると\[ \frac{\mathrm{ AP } }{\mathrm{ PD } }=\dfrac{\myBox{オ} }{\myBox{カ} } \]である。 $\mathrm{ AD }=\dfrac{\sqrt{\myBox{キク} }}{\myBox{ケ} }$ であるから、 $\mathrm{ PD }=\dfrac{\sqrt{\myBox{コサ} }}{\myBox{シ} }$ である。また、 $\cos\angle \mathrm{ ADB }=\dfrac{\sqrt{\myBox{スセ} }}{\myBox{ソタ} }$ である。
解説
図は次のようになっています。
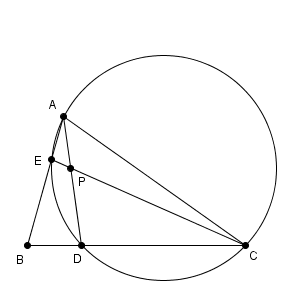
$\triangle \mathrm{ ABD }$ と直線 CE に対してメネラウスの定理を用いると
\begin{eqnarray}
\frac{\mathrm{EB} }{\mathrm{AE} }\cdot\frac{\mathrm{CD} }{\mathrm{BC} }\cdot\frac{\mathrm{PA} }{\mathrm{DP} } &=& 1 \\[5pt]
\frac{\frac{2}{3}\sqrt{6} }{\sqrt{6}-\frac{2}{3}\sqrt{6} }\cdot\frac{3}{4}\cdot\frac{\mathrm{AP} }{\mathrm{PD} } &=& 1 \\[5pt]
\frac{2}{1}\cdot\frac{3}{4}\cdot\frac{\mathrm{AP} }{\mathrm{PD} } &=& 1 \\[5pt]
\frac{\mathrm{AP} }{\mathrm{PD} } &=& \frac{2}{3} \\[5pt]
\end{eqnarray}と求められます。
余弦定理より、
\begin{eqnarray}
\mathrm{ AD }^2
&=&
\mathrm{ BA }^2+\mathrm{ BD }^2-2\mathrm{ BA }\cdot \mathrm{ BD }\cos\angle \mathrm{ ABD } \\[5pt]
&=&
6+1-2\sqrt{6}\cdot \frac{\sqrt{6} }{9} \\[5pt]
&=&
7-\frac{4}{3} \\[5pt]
&=&
\frac{17}{3} \\[5pt]
\end{eqnarray}だから、 $\mathrm{ AD }=\dfrac{\sqrt{17} }{\sqrt{3} }=\dfrac{\sqrt{51} }{3}$ となるため、\[ \mathrm{ PD }=\mathrm{ AD }\cdot \frac{3}{5}=\frac{\sqrt{51} }{5} \]となります。
また、三角形 ADB について、余弦定理より
\begin{eqnarray}
\cos\angle \mathrm{ ADB }
&=&
\frac{\mathrm{ AD }^2+\mathrm{ DB }^2-\mathrm{ AB }^2}{2\cdot \mathrm{ AD }\cdot \mathrm{ DB } } \\[5pt]
&=&
\frac{\frac{17}{3}+1-6}{2\cdot \frac{\sqrt{51} }{3} } \\[5pt]
&=&
\frac{\frac{2}{3} }{\frac{2\sqrt{51} }{3} } \\[5pt]
&=&
\frac{1}{\sqrt{51} } \\[5pt]
&=&
\frac{\sqrt{51} }{51} \\[5pt]
\end{eqnarray}となります。
解答
オカ:23
キクケ:513
コサシ:515
スセソタ:5151
解答編 つづき
次に、 $\triangle \mathrm{ AEP }$ の外接円と直線 BP の交点で、点 P とは異なる点を L とする。\[ \mathrm{ BP }\cdot \mathrm{ BL }=\myBox{チ} \]である。
解説
図は次のようになっています。
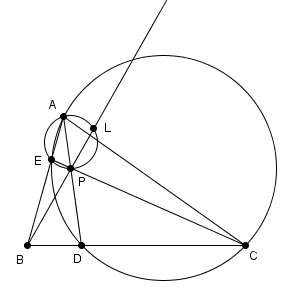
方べきの定理より、\[ \mathrm{ BP }\cdot \mathrm{ BL }=\mathrm{ BE }\cdot \mathrm{ BA }=4 \]となります。
解答編 つづき
\[ \mathrm{ BD }\cdot \mathrm{ BC }=4 \]であるから、 $\tan\angle \mathrm{ BLC }=\myBox{ツ}\sqrt{\myBox{テ} }$ である。
解説
先ほどの計算から、 $\mathrm{ BP }\cdot \mathrm{ BL }=4$ であり、 $\mathrm{ BD }\cdot \mathrm{ BC }=4$ も成り立つので、方べきの定理の逆から、4点 C, D, P, L は同一円周上にあることがわかります。次の図の青い円のように、4点を通る円がかけます。

これより、 $\angle \mathrm{ BLC }$ は、 $\angle \mathrm{ ADB }$ と等しいことがわかります。先ほど、この余弦の値を求めていたので、相互関係から
\begin{eqnarray}
1+\tan^2\angle \mathrm{ ADB } &=& \frac{1}{\cos^2\angle\mathrm{ ADB } } \\[5pt]
1+\tan^2\angle \mathrm{ ADB } &=& 51 \\[5pt]
\tan^2\angle \mathrm{ ADB } &=& 50 \\[5pt]
\end{eqnarray}となります。 $\cos\mathrm{ ADB }$ が正だったので、 $\tan \angle \mathrm{ ADB }$ も正だから、 $\tan\angle \mathrm{ ADB }=5\sqrt{2}$ となります。よって、\[ \tan\angle \mathrm{ BLC }=5\sqrt{2} \]と求められます。
解答
ツテ:52





