センター試験 数学I・数学A 2019年度追試 第1問 [1] 解説
【必答問題】
問題編
問題
a を実数とする。x の関数\[ f(x)=(1+\sqrt{2})x-\sqrt{3}a \]を考える。
(1) $f(0)\leqq 6$ となるような a の値の範囲は\[ a\geqq\myBox{アイ} \sqrt{\myBox{ウ} } \]であり、 $f(6)\geqq 0$ となるような a の値の範囲は\[ a\leqq \myBox{エ}\sqrt{\myBox{オ} }+\myBox{カ}\sqrt{\myBox{キ} } \]である。ただし、 $\mybox{エ}\sqrt{\mybox{オ} }$, $\mybox{カ}\sqrt{\mybox{キ} }$ の解答の順序は問わない。
(2) 数直線において、実数 $\mybox{アイ}\sqrt{\mybox{ウ} }$ を表す点を P とし、実数 $\mybox{エ}\sqrt{\mybox{オ} }+\mybox{カ}\sqrt{\mybox{キ} }$ を表す点を Q とするとき、線分 PQ の中点に対応する実数は $\sqrt{\myBox{ク} }$ である。
(3) 一般に、実数 u と、0以上の実数 r に対し\[ |u|\leqq r \iff -r\leqq u \leqq r \]が成り立つことに注意すると、 $f(0)\leqq 6$ かつ $f(6)\geqq 0$ となるような a の値の範囲は、絶対値を含む不等式\[ \left|a-\sqrt{\myBox{ケ} } \right| \leqq \sqrt{\myBox{コ} } + \myBox{サ}\sqrt{\myBox{シ} } \]を満たす a の値の範囲に一致する。
考え方
(1)は、一次不等式、根号の計算です。(2)は、中点の座標を求める式がわからなくても、数直線をかけば思いつけるでしょう。
(3)は、(2)との関係がわからなくても、解答の式から考えて求めることもできます。
【必答問題】
解答編
問題
a を実数とする。x の関数\[ f(x)=(1+\sqrt{2})x-\sqrt{3}a \]を考える。
(1) $f(0)\leqq 6$ となるような a の値の範囲は\[ a\geqq\myBox{アイ} \sqrt{\myBox{ウ} } \]であり、 $f(6)\geqq 0$ となるような a の値の範囲は\[ a\leqq \myBox{エ}\sqrt{\myBox{オ} }+\myBox{カ}\sqrt{\myBox{キ} } \]である。ただし、 $\mybox{エ}\sqrt{\mybox{オ} }$, $\mybox{カ}\sqrt{\mybox{キ} }$ の解答の順序は問わない。
解説
$f(0)\leqq 6$ となる $a$ の値の範囲は
\begin{eqnarray}
f(0) &\leqq& 6 \\[5pt]
-\sqrt{3}a & \leqq& 6 \\[5pt]
a & \geqq& \frac{6}{-\sqrt{3} }=-2\sqrt{3} \\[5pt]
\end{eqnarray}となります。
次に、 $f(6)\geqq 0$ となる $a$ の値の範囲を考えます。 $f(6)=6(1+\sqrt{2})-\sqrt{3}a$ なので、
\begin{eqnarray}
f(6) &\geqq& 0 \\[5pt]
6(1+\sqrt{2})-\sqrt{3}a & \geqq& 0 \\[5pt]
-\sqrt{3}a & \geqq& -6(1+\sqrt{2}) \\[5pt]
a & \leqq& \frac{-6(1+\sqrt{2})}{-\sqrt{3} } \\[5pt]
&=& 2\sqrt{3}(1+\sqrt{2}) \\[5pt]
&=& 2\sqrt{3}+2\sqrt{6} \\[5pt]
\end{eqnarray}となります。
解答
アイウ:-23
エオ・カキ:23・26
解答編 つづき
(2) 数直線において、実数 $\mybox{アイ}\sqrt{\mybox{ウ} }$ を表す点を P とし、実数 $\mybox{エ}\sqrt{\mybox{オ} }+\mybox{カ}\sqrt{\mybox{キ} }$ を表す点を Q とするとき、線分 PQ の中点に対応する実数は $\sqrt{\myBox{ク} }$ である。
解説

中点に対応する実数は、両端に対応する実数を足して2で割ると求められます。なので、\[ \frac{-2\sqrt{3}+(2\sqrt{3}+2\sqrt{6})}{2}=\sqrt{6} \]となります。
足して2で割って求められる理由は、次の通りです。2点 P, Q に対応する実数を $p, q$ とおきます(p のほうが小さいとします。)。中点に対応する実数を $m$ とおきます。
中点とは、2点からの距離が等しい点なので、 $q-m=m-p$ が成り立ちます。これを変形すると $m=\dfrac{p+q}{2}$ となります。こうして、足して2で割れば、中点に対応する実数が求められることがわかります。
解答
ク:6
解答編 つづき
(3) 一般に、実数 u と、0以上の実数 r に対し\[ |u|\leqq r \iff -r\leqq u \leqq r \]が成り立つことに注意すると、 $f(0)\leqq 6$ かつ $f(6)\geqq 0$ となるような a の値の範囲は、絶対値を含む不等式\[ \left|a-\sqrt{\myBox{ケ} } \right| \leqq \sqrt{\myBox{コ} } + \myBox{サ}\sqrt{\myBox{シ} } \]を満たす a の値の範囲に一致する。
解説
(1)の結果から、 $f(0)\leqq 6$ かつ $f(6)\geqq 0$ となるような a の値の範囲は、\[ -2\sqrt{3} \leqq a \leqq 2\sqrt{3}+2\sqrt{6} \]となります。これと同じ範囲になる、絶対値を含む不等式を考えます。
まずは、解答欄から考えてみます。式が長いので、次のような形に置き換えてみます。\[ |a-b|\leqq c \]問題文のヒントを使うと、これは\[ -c \leqq a-b \leqq c \]と同値だということがわかります。さらに各辺に $b$ を足せば、\[ -c+b \leqq a \leqq c+b \]となります。これにあうように、 $b,c$ を求めればいいことがわかります。
一番左の辺と一番右の辺を足すと、 $2b=2\sqrt{6}$ であることがわかり、 $b=\sqrt{6}$ と求められます。これより、 $c=\sqrt{6}+2\sqrt{3}$ となることがわかります。こうして、\[ |a-\sqrt{6}| \leqq \sqrt{6}+2\sqrt{3} \]が求めたい不等式であったことがわかります。
この解き方は少し天下り的ですが、絶対値の性質をよく理解していれば、次のように解けます。
絶対値とは、数直線上での距離のことです。 $|x|$ なら、 $x$ に対応する点と原点との距離であり、 $|m-n|$ なら、 $m$, $n$ に対応する点の間の距離です。
(2)で求めたことから、線分 PQ に対応する部分は、中点からの距離が $\dfrac{\mathrm{ PQ } }{2}$ 以内の部分である、といえます。中点に対応する実数が $\sqrt{6}$ であり、ここから Q までの距離は $\sqrt{6}+2\sqrt{3}$ なのだから、線分 PQ にあたる部分を式で表せば、\[ |a-\sqrt{6}| \leqq \sqrt{6}+2\sqrt{3} \]であることがわかります。
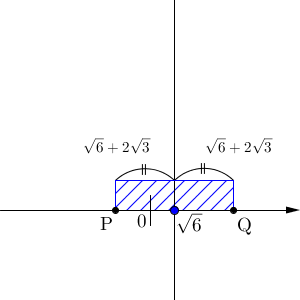
(2)で求めた中点は、絶対値の中の部分を求めていたことになります。





