センター試験 数学I・数学A 2018年度追試 第5問 [1] 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
円に内接する四角形 ABCD の辺 AB の端点 A 側の延長と辺 CD の端点 D の側の延長が点 P で交わるとする。さらに、 $\mathrm{ PA }=x$, $\mathrm{ PB }=\sqrt{10}$ および $\mathrm{ PD }=1$ とする。このとき\[ \mathrm{ CD }=\sqrt{\myBox{アイ} }\ x-\myBox{ウ} \]である。
対角線 AC と BD の交点を Q、直線 PQ と辺 BC の交点を R とし\[
\dfrac{\mathrm{ RC } }{\mathrm{ BR } }=2 \]とする。このとき\[ x=\dfrac{\myBox{エ}\sqrt{\myBox{オカ} }}{\myBox{キ} } \]である。
考え方
第5問は2つに分かれていて、前半のパートは問題数が少ないです。定理を適用して後は計算するだけです。図も計算もそれほど複雑ではなく、ひねっている箇所はありません。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
円に内接する四角形 ABCD の辺 AB の端点 A 側の延長と辺 CD の端点 D の側の延長が点 P で交わるとする。さらに、 $\mathrm{ PA }=x$, $\mathrm{ PB }=\sqrt{10}$ および $\mathrm{ PD }=1$ とする。このとき\[ \mathrm{ CD }=\sqrt{\myBox{アイ} }\ x-\myBox{ウ} \]である。
解説
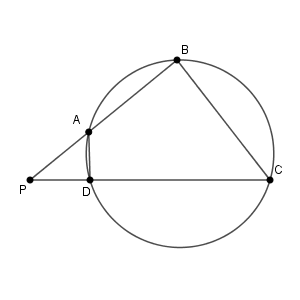
方べきの定理から
\begin{eqnarray}
\mathrm{ PA }\cdot \mathrm{ PB } &=& \mathrm{ PC } \cdot \mathrm{ PD } \\[5pt]
x\cdot\sqrt{10} &=& \mathrm{ PC } \cdot 1 \\[5pt]
\mathrm{ PC } &=& \sqrt{10}x \\[5pt]
\end{eqnarray}なので、 $\mathrm{ CD }=\mathrm{ PC }-\mathrm{ PD }=\sqrt{10}x-1$ です。
解答
アイウ:101
解答編 つづき
問題
対角線 AC と BD の交点を Q、直線 PQ と辺 BC の交点を R とし\[
\dfrac{\mathrm{ RC } }{\mathrm{ BR } }=2 \]とする。このとき\[ x=\dfrac{\myBox{エ}\sqrt{\myBox{オカ} }}{\myBox{キ} } \]である。
解説
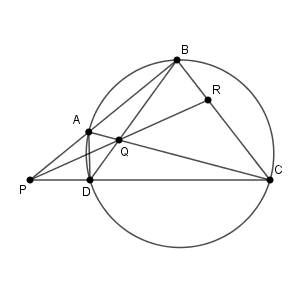
チェバの定理から
\begin{eqnarray}
\frac{\mathrm{BA} }{\mathrm{AP} } \cdot \frac{\mathrm{PD} }{\mathrm{DC} } \cdot \frac{\mathrm{CR} }{\mathrm{RB} } &=& 1 \\[5pt]
\frac{\sqrt{10}-x}{x} \cdot \frac{1}{\sqrt{10}x-1} \cdot 2 &=& 1 \\[5pt]
2\sqrt{10}-2x &=& \sqrt{10}x^2-x \\[5pt]
\sqrt{10}x^2 +x -2\sqrt{10} &=& 0 \\[5pt]
\end{eqnarray}となります。これより、 $x$ は
\begin{eqnarray}
x &=& \frac{-1\pm\sqrt{1^2-4\sqrt{10}\cdot(-2\sqrt{10})} }{2\sqrt{10} } \\[5pt]
&=& \frac{-1\pm 9}{2\sqrt{10} } \\[5pt]
\end{eqnarray}です。 $x\gt 0$ なので、
\begin{eqnarray}
x
&=&
\dfrac{-1+9}{2\sqrt{10} } \\[5pt]
&=&
\dfrac{8\sqrt{10} }{20} \\[5pt]
&=&
\dfrac{2\sqrt{10} }{5} \\[5pt]
\end{eqnarray}となります。
解答
エオカキ:2105





