センター試験数学I・数学A 2018年度追試第1問 [2] 解説

🕒 2020/07/09 🔄 2023/05/01

【必答問題】

問題編

問題

　$a$ を正の実数とする。このとき、実数 $x$ に関する次の条件 $p,q,r$ を考える。
\begin{eqnarray} \ p &:& |x-1|\leqq a, \\[5pt] \ q &:& |x|\leqq \frac{5}{2}, \\[5pt] \ r &:& x^2-2x\leqq a \\[5pt] \end{eqnarray}
(1) 次の $\mybox{シ}$, $\mybox{ス}$ に当てはまるものを、下の 0 ～ 3 のうちからそれぞれ一つ選べ。ただし、同じものを繰り返し選んでもよい。

　$a=1$ のとき、 $p$ は $q$ であるための $\myBox{シ}$ 。また、 $a=3$ のとき、 $p$ は $q$ であるための $\myBox{ス}$

　0: 必要条件であるが、十分条件ではない
　1: 十分条件であるが、必要条件ではない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

(2) 命題「 $p \implies q$ 」が真となるような $a$ の最大値は $\dfrac{\myBox{セ} }{\myBox{ソ} }$ である。また、命題「 $q \implies p$ 」が真となるような $a$ の最小値は $\dfrac{\myBox{タ} }{\myBox{チ} }$ である。

(3) 命題「 $r \implies q$ 」が真となるような $a$ の最大値は $\dfrac{\myBox{ツ} }{\myBox{テ} }$ である。

考え方

$a$ の値によって、条件 $p$ を満たす範囲が変わります。これに加え、命題と集合の関係を考えながら解いていく問題です。数直線をかいて考えるといいでしょう。

最後に突然出てくる $r$ は少し難しいです。条件 $p$ と似た形に変形する方法もありますし、二次関数のグラフを使って解くこともできますが、ハードルは高めです。

【必答問題】

解答編

問題

　$a$ を正の実数とする。このとき、実数 $x$ に関する次の条件 $p,q,r$ を考える。
\begin{eqnarray} \ p &:& |x-1|\leqq a, \\[5pt] \ q &:& |x|\leqq \frac{5}{2}, \\[5pt] \ r &:& x^2-2x\leqq a \\[5pt] \end{eqnarray}
(1) 次の $\mybox{シ}$, $\mybox{ス}$ に当てはまるものを、下の 0 ～ 3 のうちからそれぞれ一つ選べ。ただし、同じものを繰り返し選んでもよい。

　$a=1$ のとき、 $p$ は $q$ であるための $\myBox{シ}$ 。また、 $a=3$ のとき、 $p$ は $q$ であるための $\myBox{ス}$

　0: 必要条件であるが、十分条件ではない
　1: 十分条件であるが、必要条件ではない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

解説

$a=1$ のとき、条件 $p$ は
\begin{equation} |x-1| \leqq 1 \\[5pt] -1\leqq x-1 \leqq 1 \\[5pt] 0 \leqq x \leqq 2 \\[5pt] \end{equation}と同値です。条件 $q$ は $-\dfrac{5}{2}\leqq x \leqq \dfrac{5}{2}$ と言い換えられます。

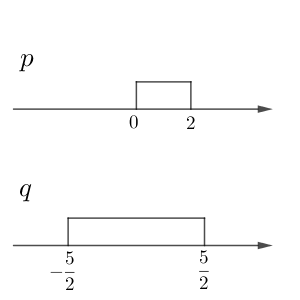
これより、 $p$ が成り立てば $q$ も成り立ちます（ $p$ に対応する範囲に入っていたら $q$ に対応する範囲にも入っている）が、逆は成り立ちません。そのため、 $p$ は $q$ であるための十分条件であるが、必要条件ではないことがわかります。

$a=3$ のとき、条件 $p$ は
\begin{equation} |x-1| \leqq 3 \\[5pt] -3\leqq x-1 \leqq 3 \\[5pt] -2 \leqq x \leqq 4 \\[5pt] \end{equation}と同値です。

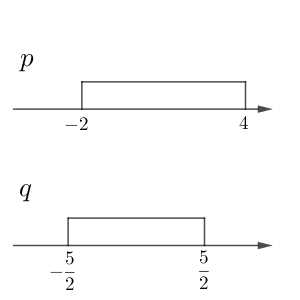
これより、 $p\implies q$ は成り立ちません（反例は $x=4$ ）し、 $q\implies p$ も成り立ちません（反例は $x=-\dfrac{5}{2}$ ）。よって、必要条件でも十分条件でもないことがわかります。

解答

シス：13

解答編つづき

問題

(2) 命題「 $p \implies q$ 」が真となるような $a$ の最大値は $\dfrac{\myBox{セ} }{\myBox{ソ} }$ である。また、命題「 $q \implies p$ 」が真となるような $a$ の最小値は $\dfrac{\myBox{タ} }{\myBox{チ} }$ である。

解説

条件 $p$ は
\begin{equation} |x-1| \leqq a \\[5pt] -a\leqq x-1 \leqq a \\[5pt] -a+1 \leqq x \leqq a+1 \\[5pt] \end{equation}と同値です。

$p\implies q$ が真となることは、 $-a+1\geqq -\dfrac{5}{2}$ かつ $a+1\leqq \dfrac{5}{2}$ が成り立つことと同値です。これを両方満たすのは、 $a\leqq \dfrac{3}{2}$ なので、最大値は $\dfrac{3}{2}$ です。

$q\implies p$ が真となることは、 $-a+1\leqq -\dfrac{5}{2}$ かつ $a+1\geqq \dfrac{5}{2}$ が成り立つことと同値です。これを両方満たすのは、 $a\geqq \dfrac{7}{2}$ なので、最小値は $\dfrac{7}{2}$ です。

解答

セソ：32
タチ：72

解答編つづき

問題

(3) 命題「 $r \implies q$ 」が真となるような $a$ の最大値は $\dfrac{\myBox{ツ} }{\myBox{テ} }$ である。

解説

最後にだけ突然出てくる $r$ ですが、 $p$ のときと似たような感じで解くなら、次のように変形することになるでしょう。
\begin{equation} x^2-2x \leqq a \\[5pt] x^2-2x+1 \leqq a+1 \\[5pt] |x-1| \leqq \sqrt{a+1} \\[5pt] \end{equation}これだと、条件 $p$ と似た形になるので、(2)と同じように解けます。さらに変形して \begin{equation} -\sqrt{a+1} \leqq x-1 \leqq \sqrt{a+1} \\[5pt] -\sqrt{a+1}+1 \leqq x \leqq \sqrt{a+1}+1 \\[5pt] \end{equation}となります。

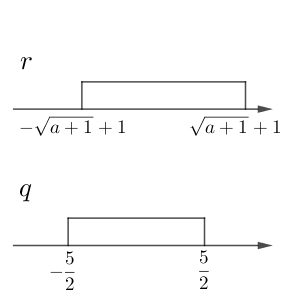
$r \implies q$ が成り立つことは、 $-\sqrt{a+1}+1\geqq -\dfrac{5}{2}$ かつ $\sqrt{a+1}+1\leqq \dfrac{5}{2}$ が成り立つことと同値です。両方を満たすのは $\sqrt{a+1}\leqq \dfrac{3}{2}$ のときなので、 $a\leqq \dfrac{5}{4}$ が成り立つことと同値です。よって、最大値は $\dfrac{5}{4}$ となります。

また、別の解き方として、二次関数の問題として解くこともできます。 $x^2-2x\leqq a$ の範囲は、 $y=x^2-2x$ と $y=a$ のグラフを比較して考えることができます。