センター試験 数学I・数学A 2018年度追試 第1問 [3] 解説

【必答問題】

問題編

問題

　実数 $a$ は2次不等式 $a^2-3\lt a$ を満たすとする。このとき $a$ のとり得る値の範囲は\[
\frac{\myBox{ト}-\sqrt{\myBox{ナニ} }}{\myBox{ヌ} }\lt a \lt \frac{\mybox{ト}+\sqrt{\mybox{ナニ} }}{\mybox{ヌ} } \]である。

　$x$ の2次関数\[ f(x)=-x^2+1 \]を考える。

　$a^2-3\leqq x\leqq a$ における関数 $y=f(x)$ の最大値が $1$ であるような $a$ の値の範囲は\[ \myBox{ネ}\leqq a \leqq \sqrt{\myBox{ノ} } \]である。

　また、 $a^2-3\leqq x\leqq a$ における関数 $y=f(x)$ の最大値が $1$ で、最小値が $f(a)$ であるような $a$ の値の範囲は\[ \frac{\myBox{ハヒ}+\sqrt{\myBox{フヘ} }}{\myBox{ホ} } \leqq a \leqq \sqrt{\mybox{ノ} } \]である。

考え方

1つ目は標準的な二次不等式の問題です。2つ目は、最大値が $1$ となるのは、区間がどうなっているときかを考えます。

最後は少し難しいです。左端での値と右端での値を比較すればいいのですが、それは難しいので別の方法を考えます。関数の値を直接使わずに最小値について考えるために条件をどう言い換えるかがポイントになります。

【必答問題】

解答編

問題

　実数 $a$ は2次不等式 $a^2-3\lt a$ を満たすとする。このとき $a$ のとり得る値の範囲は\[
\frac{\myBox{ト}-\sqrt{\myBox{ナニ} }}{\myBox{ヌ} }\lt a \lt \frac{\mybox{ト}+\sqrt{\mybox{ナニ} }}{\mybox{ヌ} } \]である。

解説

$a^2-3=a$ とすると
\begin{eqnarray} a^2-a-3 &=& 0\\[5pt] a&=&\frac{1\pm\sqrt{13} }{2} \end{eqnarray}となります。

これより、 $a^2-3\lt a$ となる範囲は\[ \frac{1-\sqrt{13} }{2} \lt a \lt \frac{1+\sqrt{13} }{2} \]となります。

解答

トナニヌ：1132

解答編 つづき

問題

　$x$ の2次関数\[ f(x)=-x^2+1 \]を考える。

　$a^2-3\leqq x\leqq a$ における関数 $y=f(x)$ の最大値が $1$ であるような $a$ の値の範囲は\[ \myBox{ネ}\leqq a \leqq \sqrt{\myBox{ノ} } \]である。

解説

$x$ の定義域が実数全体であれば、 $f(x)=-x^2+1$ の最大値は $1$ です。この値をとるのは $x=0$ のときだけなので、 $a^2-3\leqq x\leqq a$ の範囲で $y=f(x)$ の最大値が $1$ となることは、この範囲に $0$ が含まれていること、つまり、 $a^2-3\leqq 0\leqq a$ と同値です。

左側から $-\sqrt{3}\leqq a \leqq \sqrt{3}$ であり、右側から $a\geqq 0$ なので、両方を満たす範囲は $0\leqq a\leqq \sqrt{3}$ となります。

なお、 $a^2-3\leqq 0\leqq a$ を満たしているときは $a^2-3\leqq a$ は自動的に満たされます。

解答

ネノ：03

解答編 つづき

問題

　また、 $a^2-3\leqq x\leqq a$ における関数 $y=f(x)$ の最大値が $1$ で、最小値が $f(a)$ であるような $a$ の値の範囲は\[ \frac{\myBox{ハヒ}+\sqrt{\myBox{フヘ} }}{\myBox{ホ} } \leqq a \leqq \sqrt{\mybox{ノ} } \]である。

解説

今度は最大値に関する条件以外に、「最小値は区間の右端での値に等しい」という条件がついています。最大値が $1$ という状況の下で、最小値について考えます。

最小値となるのは、区間の右端か左端です。なので、最小値が $f(a)$ となるのは、右端での値が左端での値以下となるときです。

ただ、 $f(a)$ と $f(a^2-3)$ を比較するのは大変です。そこで、別の方法を考えます。放物線は左右対称であり、上に凸の場合は、放物線の軸から離れるほど下に行くので、軸からの距離に着目すればいいです。

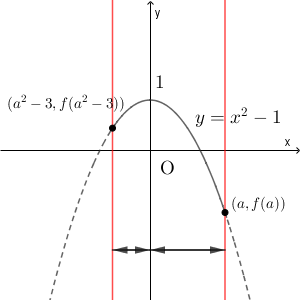
放物線の軸（今の場合は $y$ 軸）から区間の右端までの距離は $a$ です。一方、区間の左端までの距離は $-(a^2-3)$ です。 $a^2-3$ の値は $0$ 以下なので、距離を考えるときはマイナスをつけます。

区間の右端での値が左端での値以下となるのは、軸から右端までの距離が左端までの距離以上のときであり、このとき以外にはないので\[ a\geqq -a^2+3 \]を解けばいいことがわかります。

$a^2+a-3=0$ を解くと、 $a=\dfrac{-1\pm\sqrt{13} }{2}$ なので、
\begin{eqnarray} a\geqq -a^2+3 \\[5pt] a^2+a-3 \geqq 0 \\[5pt] a \leqq \dfrac{-1-\sqrt{13} }{2},\ a \geqq \dfrac{-1+\sqrt{13} }{2} \\[5pt] \end{eqnarray}となります。

これと、「最大値が $1$ 」となる条件 $0\leqq a\leqq \sqrt{3}$ との共通部分を考えます。 $\sqrt{13}\gt 0$ なので $\dfrac{-1+\sqrt{13} }{2}\gt 0$ です。また、
\begin{eqnarray} \dfrac{-1+\sqrt{13} }{2} \leqq \dfrac{-1+\sqrt{16} }{2}=\frac{3}{2} \end{eqnarray}なので、 $\dfrac{-1+\sqrt{13} }{2}\lt \sqrt{3}$ です。

以上から、 $a$ の範囲は\[ \dfrac{-1+\sqrt{13} }{2} \leqq a\leqq \sqrt{3} \]となります。

解答

ハヒフヘホ：-1132