センター試験 数学I・数学A 2018年度追試 第2問 [1] 解説
【必答問題】
問題編
問題
$\triangle \mathrm{ABC}$ は $\mathrm{AB}=4$, $\mathrm{BC}=10\sqrt{3}$, $\mathrm{AC}=14$ を満たす。
(1) $\cos\angle \mathrm{B}=\dfrac{\sqrt{\myBox{ア} }}{\myBox{イ} }$ である。辺 BC 上に点 D を取り、 $\triangle \mathrm{ABD}$ の外接円の半径を $R$ とするとき、 $\dfrac{\mathrm{AD} }{R}=\myBox{ウ}$ であり、点 D を点 B から点 C まで移動させるとき、 $R$ の最小値は $\myBox{エ}$ である。ただし、点 D は点 B とは異なる点とする。
(2) $\triangle \mathrm{ABD}$ の外接円の中心が辺 BC 上にあるとき、 $R=\dfrac{\myBox{オ}\sqrt{\myBox{カ} }}{\myBox{キ} }$ であり、 $\triangle \mathrm{ACD}$ の面積は $\dfrac{\myBox{クケ}\sqrt{\myBox{コ} }}{\myBox{サ} }$ である。
考え方
角度も辺の長さも複雑ではないので、計算は軽めです。それぞれの状況に応じた図がきちんとかけるかがポイントになります。計算だけで解くのではなく、図を使って考えるようにしましょう。
【必答問題】
解答編
問題
$\triangle \mathrm{ABC}$ は $\mathrm{AB}=4$, $\mathrm{BC}=10\sqrt{3}$, $\mathrm{AC}=14$ を満たす。
(1) $\cos\angle \mathrm{B}=\dfrac{\sqrt{\myBox{ア} }}{\myBox{イ} }$ である。
解説
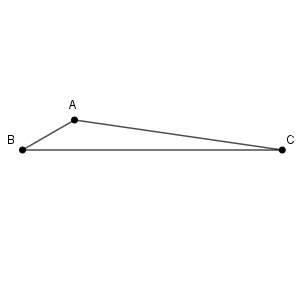
三辺がわかっているので、余弦定理を使います。
\begin{eqnarray}
\cos\angle\mathrm{B}
&=&
\dfrac{\mathrm{AB}^2+\mathrm{BC}^2-\mathrm{AC}^2}{2\cdot \mathrm{AB}\cdot \mathrm{BC} } \\[5pt]
&=&
\dfrac{16+300-196}{2\cdot 4\cdot 10\sqrt{3} } \\[5pt]
&=&
\dfrac{120}{80\sqrt{3} } \\[5pt]
&=&
\dfrac{\sqrt{3} }{2} \\[5pt]
\end{eqnarray}となります。
解答
アイ:32
解答編 つづき
問題
辺 BC 上に点 D を取り、 $\triangle \mathrm{ABD}$ の外接円の半径を $R$ とするとき、 $\dfrac{\mathrm{AD} }{R}=\myBox{ウ}$ であり、点 D を点 B から点 C まで移動させるとき、 $R$ の最小値は $\myBox{エ}$ である。ただし、点 D は点 B とは異なる点とする。
解説
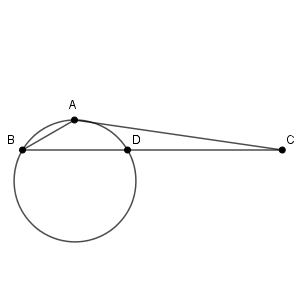
$\cos\angle\mathrm{B}=\dfrac{\sqrt{3} }{2}$ なので、 $\angle \mathrm{B}=30^{\circ}$ です。正弦定理から
\begin{eqnarray}
\dfrac{\mathrm{AD} }{\sin\angle\mathrm{B} } &=& 2R \\[5pt]
\dfrac{\mathrm{AD} }{R} &=& 2\cdot \sin30^{\circ}=1 \\[5pt]
\end{eqnarray}となります。
$R=\mathrm{AD}$ なので、 $R$ が最小となるのは、 AD が最小となるときです。つまり、AD と BC が垂直のときです。このとき、三角形 ABD は、30度60度90度の直角三角形なので、\[ \mathrm{AD}=4\div2=2 \]となります。
以上から、 $R$ の最小値は $2$ です。
解答
ウ:1
エ:2
解答編 つづき
問題
(2) $\triangle \mathrm{ABD}$ の外接円の中心が辺 BC 上にあるとき、 $R=\dfrac{\myBox{オ}\sqrt{\myBox{カ} }}{\myBox{キ} }$ であり、 $\triangle \mathrm{ACD}$ の面積は $\dfrac{\myBox{クケ}\sqrt{\myBox{コ} }}{\myBox{サ} }$ である。
解説
$\triangle \mathrm{ ABD }$ の外接円の中心が辺 BC 上にあるとき、図は次のようになります。
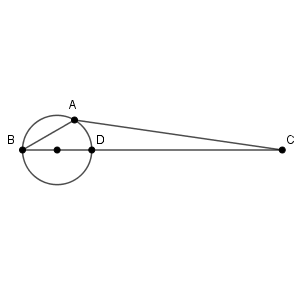
線分 BD が外接円の直径になり、\[ \mathrm{ BD }\cos\angle \mathrm{ B }=\mathrm{ AB } \]となります。これより
\begin{eqnarray}
R &=& \dfrac{\mathrm{ BD } }{2} \\[5pt]
&=& \dfrac{\mathrm{AB} }{\cos\angle\mathrm{B} }\cdot \dfrac{1}{2} \\[5pt]
&=& \dfrac{4}{\frac{\sqrt{3} }{2} }\cdot \dfrac{1}{2} \\[5pt]
&=& \dfrac{4}{\sqrt{3} } \\[5pt]
&=& \dfrac{4\sqrt{3} }{3} \\[5pt]
\end{eqnarray}となります。
次に、三角形 ACD の面積を考えます。 CD の長さは\[ 10\sqrt{3}-\dfrac{4\sqrt{3} }{3}\cdot2=\dfrac{22\sqrt{3} }{3} \]です。また、 CD を底辺と考えたときの高さは\[ \mathrm{ AB }\sin\angle\mathrm{B}=2 \]なので、面積は\[ \dfrac{22\sqrt{3} }{3}\times 2\div2=\dfrac{22\sqrt{3} }{3} \]となります。
解答
オカキ:433
クケコサ:2233





