センター試験 数学I・数学A 2018年度追試 第2問 [2] 解説
問題文中の画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
高校生のKさんは、ニュースで「為替レート(1米ドルは何円か)」および「日経平均株価」と呼ばれている数値が日々変化していることに興味をもったので、これらの数値を入手して調べてみることにした。
為替レートを100で割ったものを $X$ とする。例えば、1米ドルが123円のとき $X$ は $1.23$ となる。また、日経平均株価を10,000で割ったものを $Y$ とする。例えば、日経平均株価が16,500円のとき $Y$ は $1.65$ となる。
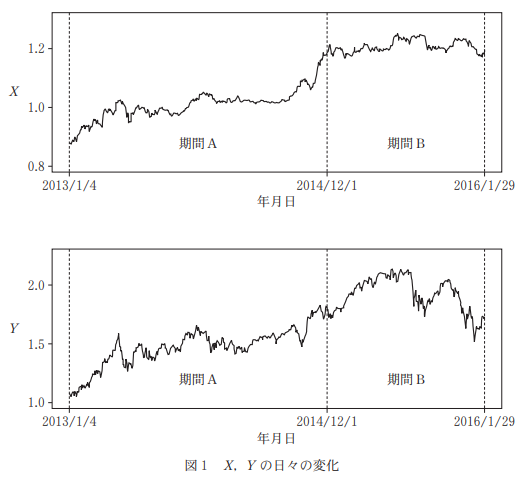
図1は、 $X, Y$ の日々の変化を描いたものである。ただし、土曜日、日曜日、祝日などデータのない日は除いている。全期間を次の二つの期間に分けて考察する。
期間A:2013年1月4日~2014年11月28日(468日分のデータ)
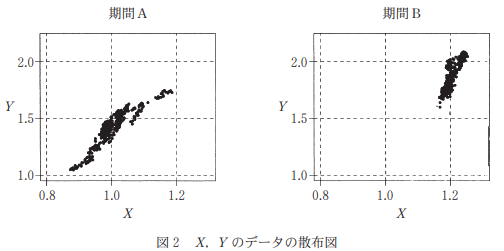
期間B:2014年12月1日~2016年1月29日(284日分のデータ)図2は、期間Aと期間Bにおける $X, Y$ のデータの散布図である。
(1) 表1は、 $X$ と $Y$ について平均値、標準偏差および共分散を計算し、有効数字3桁で表したものである。ただし、 $X$ と $Y$ の共分散とは、 $X$ の偏差と $Y$ の偏差の積の平均値である。
表1 平均値、標準偏差および共分散 期間A 期間B 全期間 $X$ の平均値 $1.01$ $1.21$ $1.08$ $Y$ の平均値 $1.44$ $1.90$ $1.61$ $X$ の標準偏差 $0.0522$ $0.0209$ $0.105$ $Y$ の標準偏差 $0.144$ $0.118$ $0.260$ $X$ と $Y$ の共分散 $0.00685$ $0.00203$ $0.0263$ 次の $\mybox{シ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
表1を用いて、期間A、期間Bにおける $X$ と $Y$ の相関係数を求め、小数第3位を四捨五入すると、それぞれ $0.91$ と $0.82$ である。全期間における $X$ と $Y$ の相関係数を $r$ とすると $\myBox{シ}$ である。
0: $r\leqq 0$
1: $0\lt r\lt 0.82$
2: $r=0.82$
3: $0.82\lt r \lt 0.91$
4: $r=0.91$
5: $0.91\lt r$(2) $X$ のデータの $t$ 番目の値を $x_t$ とする。期間Aに対応するのは $t=1$, $2$, $\cdots$, $468$ であり、期間Bに対応するのは $t=469$, $470$, $\cdots$, $752$ である。 $X$ が日々どのように変化しているか調べるために、次の式によって定義される $u_t$ を計算する。\[ u_t=\dfrac{x_{t+1}-x_t}{x_t}\times 100 \]ただし、期間Aの最終日( $t=468$ )と期間Bの最終日( $t=752$ )については $u_t$ を計算しない。 $u_1$, $\cdots$, $u_{467}$ および $u_{469}$, $\cdots$, $u_{751}$ を $U$ のデータと呼ぶ。
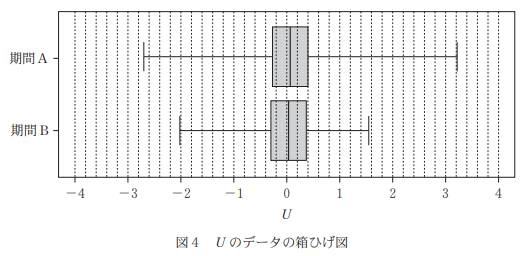
図3および図4は、期間A、期間Bにおける $U$ のデータのヒストグラム及び箱ひげ図である。期間Aにおける中央値は $0.0584$ であり、期間Bにおける中央値は $0.0252$ であった。
次の $\mybox{ス}$, $\mybox{セ}$ に当てはまるものを、下の 0 ~ 6 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図3および図4から $U$ のデータについて読み取れることとして正しいものは、 $\myBox{ス}$, $\myBox{セ}$ である。
0: 期間Aにおける最大値は、期間Bにおける最大値より小さい。
1: 期間Aにおける第1四分位数は、期間Bにおける第1四分位数より小さい。
2: 期間Aにおける四分位範囲と期間Bにおける四分位範囲の差は $0.2$ より大きい。
3: 期間Aにおける範囲は、期間Bにおける範囲より小さい。
4: 期間A、期間Bの両方において、四分位範囲は中央値の絶対値の8倍より大きい。
5: 期間Aにおいて、第3四分位数は度数が最大の階級に入っている。
6: 期間Bにおいて、第1四分位数は度数が最大の階級に入っている。
(3) $X, Y$ から $X', Y'$ を次の式によって定義する。\[ X'=aX+b,\ Y'=cY+d \]ただし、 $a,b,c,d$ は定数であり、 $a\ne 0$ かつ $c\ne 0$ とする。
次の $\mybox{ソ}$ に当てはまるものを、下の 0 ~ 8 のうちから一つ選べ。
$X'$ と $Y'$ の相関係数は、 $X$ と $Y$ の相関係数の $\myBox{ソ}$ 倍である。
0: $1$
1: $a$
2: $a^2$
3: $ac$
4: $\dfrac{ac}{|ac|}$
5: $b$
6: $b^2$
7: $bd$
8: $|bd|$
(4) 次ページの図5の三つの散布図について考える。散布図1で表される $V$ と $W$ の2種類のデータの相関係数、散布図2で表される $V'$ と $W'$ の2種類のデータの相関係数、および散布図3で表される $V^{\prime\prime}$ と $W^{\prime\prime}$ の2種類のデータの相関係数をそれぞれ $r_1$, $r_2$ および $r_3$ とする。これらは、小数第3位を四捨五入して小数第2位まで求めると、 $-0.76$, $0.10$, $0.98$ のいずれかであることがわかっている。
次の $\mybox{タ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
$r_1, r_2$ および $r_3$ の値の組合せとして正しいものは $\myBox{タ}$ である。
$r_1$ $r_2$ $r_3$ 0 $-0.76$ $0.10$ $0.98$ 1 $-0.76$ $0.98$ $0.10$ 2 $0.10$ $-0.76$ $0.98$ 3 $0.10$ $0.98$ $-0.76$ 4 $0.98$ $-0.76$ $0.10$ 5 $0.98$ $0.10$ $-0.76$
考え方
それぞれの問題は独立しているので、わからなくても次の問題を考えることができます。(3)は抽象的で難しい問題ですが、相関係数をどのように求めるかを考えましょう。
問題文中の画像は、大学入試センターのサイトから取得しています。
【必答問題】
解答編
問題
高校生のKさんは、ニュースで「為替レート(1米ドルは何円か)」および「日経平均株価」と呼ばれている数値が日々変化していることに興味をもったので、これらの数値を入手して調べてみることにした。
為替レートを100で割ったものを $X$ とする。例えば、1米ドルが123円のとき $X$ は $1.23$ となる。また、日経平均株価を10,000で割ったものを $Y$ とする。例えば、日経平均株価が16,500円のとき $Y$ は $1.65$ となる。
図1は、 $X, Y$ の日々の変化を描いたものである。ただし、土曜日、日曜日、祝日などデータのない日は除いている。全期間を次の二つの期間に分けて考察する。
期間A:2013年1月4日~2014年11月28日(468日分のデータ)
期間B:2014年12月1日~2016年1月29日(284日分のデータ)図2は、期間Aと期間Bにおける $X, Y$ のデータの散布図である。
(1) 表1は、 $X$ と $Y$ について平均値、標準偏差および共分散を計算し、有効数字3桁で表したものである。ただし、 $X$ と $Y$ の共分散とは、 $X$ の偏差と $Y$ の偏差の積の平均値である。
表1 平均値、標準偏差および共分散 期間A 期間B 全期間 $X$ の平均値 $1.01$ $1.21$ $1.08$ $Y$ の平均値 $1.44$ $1.90$ $1.61$ $X$ の標準偏差 $0.0522$ $0.0209$ $0.105$ $Y$ の標準偏差 $0.144$ $0.118$ $0.260$ $X$ と $Y$ の共分散 $0.00685$ $0.00203$ $0.0263$ 次の $\mybox{シ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
表1を用いて、期間A、期間Bにおける $X$ と $Y$ の相関係数を求め、小数第3位を四捨五入すると、それぞれ $0.91$ と $0.82$ である。全期間における $X$ と $Y$ の相関係数を $r$ とすると $\myBox{シ}$ である。
0: $r\leqq 0$
1: $0\lt r\lt 0.82$
2: $r=0.82$
3: $0.82\lt r \lt 0.91$
4: $r=0.91$
5: $0.91\lt r$
解説
相関係数は、共分散をそれぞれの標準偏差で割って求められます。なので、表の数字を使うと\[ r=\dfrac{0.0263}{0.105\times0.260} \]となります。分母は $0.0273$ なので、 $r$ を計算すると、 $0.963$ 程度だとわかります。選択肢の中では $0.91\lt r$ が正しいです。
解答
シ:5
解答編 つづき
問題
(2) $X$ のデータの $t$ 番目の値を $x_t$ とする。期間Aに対応するのは $t=1$, $2$, $\cdots$, $468$ であり、期間Bに対応するのは $t=469$, $470$, $\cdots$, $752$ である。 $X$ が日々どのように変化しているか調べるために、次の式によって定義される $u_t$ を計算する。\[ u_t=\dfrac{x_{t+1}-x_t}{x_t}\times 100 \]ただし、期間Aの最終日( $t=468$ )と期間Bの最終日( $t=752$ )については $u_t$ を計算しない。 $u_1$, $\cdots$, $u_{467}$ および $u_{469}$, $\cdots$, $u_{751}$ を $U$ のデータと呼ぶ。
図3および図4は、期間A、期間Bにおける $U$ のデータのヒストグラム及び箱ひげ図である。期間Aにおける中央値は $0.0584$ であり、期間Bにおける中央値は $0.0252$ であった。
次の $\mybox{ス}$, $\mybox{セ}$ に当てはまるものを、下の 0 ~ 6 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図3および図4から $U$ のデータについて読み取れることとして正しいものは、 $\myBox{ス}$, $\myBox{セ}$ である。
0: 期間Aにおける最大値は、期間Bにおける最大値より小さい。
1: 期間Aにおける第1四分位数は、期間Bにおける第1四分位数より小さい。
2: 期間Aにおける四分位範囲と期間Bにおける四分位範囲の差は $0.2$ より大きい。
3: 期間Aにおける範囲は、期間Bにおける範囲より小さい。
4: 期間A、期間Bの両方において、四分位範囲は中央値の絶対値の8倍より大きい。
5: 期間Aにおいて、第3四分位数は度数が最大の階級に入っている。
6: 期間Bにおいて、第1四分位数は度数が最大の階級に入っている。
解説
図が小さくて見にくいかもしれませんが、それぞれの選択肢を一つずつ見ていきます。「読み取れないもの」「読み取れるが正しくはないもの」を除外していきます。
選択肢0 は、最大値に関する内容なので、箱ひげ図を見ます。右端の値同士を見比べればよく、期間Aのほうが右側にあるので、最大値は期間Aの方が大きいです。なので、間違いです。
選択肢1 は、第1四分位数についてなので、これも箱ひげ図を見ます。箱の左端が第1四分位数に対応します。期間Aのほうが右側にあるので、期間Aのほうが第1四分位数が大きいため、これも間違いです。
選択肢2 は、四分位範囲に関するものなので、これも箱ひげ図を見ます。四分位範囲は、箱の横幅のことです。縦の点線は $0.2$ 刻みです。箱の右側はほとんど同じ値で、左側もほとんど同じ値です。四分位範囲の差が $0.2$ より大きくはないので、これも間違いです。
選択肢3 は、範囲に関するものなので、箱ひげ図を見ます。範囲は、右端から左端までの幅のことです。期間Aの方が大きいので、これも間違いです。
選択肢4 は、四分位範囲についてなので、箱ひげ図を見ます。四分位範囲は箱の横幅のことで、期間Aについてはだいたい $0.7$ くらいです。中央値は $0.0584$ と問題文にあるので、絶対値の8倍より大きいです。また、期間Bの四分位範囲もだいたい $0.7$ くらいで、中央値は $0.0252$ なので、絶対値の8倍より大きいです。なので、これは正しいことがわかります。
選択肢5 は、箱ひげ図とヒストグラムの両方を見ます。第3四分位数は、箱の右側に対応するので、期間Aの第3四分位数はだいたい $0.4$ くらいです。ヒストグラムを見ると、階級の幅は $0.5$ なので、第3四分位数は、 $0$ から $0.5$ の階級に入っています。この階級の度数が一番大きいので、これは正しいです。
選択肢6 も、箱ひげ図とヒストグラムの両方を見ます。第1四分位数は、箱の左側に対応するので、期間Bの第1四分位数はだいたい $-0.3$ くらいです。ヒストグラムを見ると、第1四分位数は、 $-0.5$ から $0$ の階級に入っています。度数が最大の階級ではないので、間違いです。
以上から、4と5が正しいことがわかります。
解答
ス・セ:4・5
解答編 つづき
問題
(3) $X, Y$ から $X', Y'$ を次の式によって定義する。\[ X'=aX+b,\ Y'=cY+d \]ただし、 $a,b,c,d$ は定数であり、 $a\ne 0$ かつ $c\ne 0$ とする。
次の $\mybox{ソ}$ に当てはまるものを、下の 0 ~ 8 のうちから一つ選べ。
$X'$ と $Y'$ の相関係数は、 $X$ と $Y$ の相関係数の $\myBox{ソ}$ 倍である。
0: $1$
1: $a$
2: $a^2$
3: $ac$
4: $\dfrac{ac}{|ac|}$
5: $b$
6: $b^2$
7: $bd$
8: $|bd|$
解説
今までの日経平均株価と為替レートとは関係のない話になっています。
相関係数をどのように求めるかを考えます。相関係数とは、共分散をそれぞれの標準偏差で割ったものです。標準偏差とは、分散の正の平方根のことでした。
$X$ の平均 $\bar{X}$ は $\dfrac{x_1+x_2+\cdots+x_n}{n}$ と書けます。一方、 $X'$ の平均 $\bar{X'}$ は
\begin{eqnarray}
\bar{X'}
&=& \dfrac{(ax_1+b)+(ax_2+b)+\cdots+(ax_n+b)}{n} \\[5pt]
&=& \dfrac{a(x_1+x_2+\cdots+x_n)+bn}{n} \\[5pt]
&=& a\bar{X}+b \\[5pt]
\end{eqnarray}となります。 $X'$ の分散は
\begin{eqnarray}
& & \dfrac{(ax_1+b-\bar{X'})^2+(ax_2+b-\bar{X'})^2+\cdots+(ax_n+b-\bar{X'})^2}{n} \\[5pt]
&=& \dfrac{(ax_1-a\bar{X})^2+(ax_2-a\bar{X})^2+\cdots+(ax_n-a\bar{X})^2}{n} \\[5pt]
&=& a^2\cdot \dfrac{(x_1-\bar{X})^2+(x_2-\bar{X})^2+\cdots+(x_n-\bar{X})^2}{n} \\[5pt]
\end{eqnarray}となり、 $X$ の分散の $a^2$ 倍になることがわかります。なので、 $X'$ の標準偏差は $X$ の標準偏差の $|a|$ 倍になります。
同じように考えれば、 $Y'$ の標準偏差は $Y$ の標準偏差の $|c|$ 倍となります。 $X'$ と $Y'$ の共分散は、分散のときと同じように計算すると、分子に\[ (ax_k+b-\bar{X'})(cy_k+d-\bar{Y'}) \]が現れます。これを変形すれば\[ ac(x_k-\bar{X})(y_k-\bar{Y}) \]となることから、 $X'$ と $Y'$ の共分散は、 $X$ と $Y$ の共分散の $ac$ 倍になることがわかります。
共分散は $ac$ 倍、標準偏差の積は $|ac|$ 倍になるので、相関係数は $\dfrac{ac}{|ac|}$ 倍になります。よって、選択肢4 が正解です。
なお、式の形から、 $a,c$ の片方だけが出てくることはありません。同様に、 $b,d$ の片方だけが出てくることもありません。なので、1, 2, 5, 6 はすぐに消去できます。
また、相関係数とは、「片方が大ならもう片方も大、片方が小ならもう片方も小」という関係がどの程度あるかを表すものです。なので、 $a=2, c=2$ として $b=d=0$ としても、相関係数は変わりません。また、 $a=1$, $c=-1$ とすると、相関係数は $-1$ 倍されます。なので、選択肢4 しかありえません。
解答
ソ:4
参考
解答編 つづき
問題
(4) 次ページの図5の三つの散布図について考える。散布図1で表される $V$ と $W$ の2種類のデータの相関係数、散布図2で表される $V'$ と $W'$ の2種類のデータの相関係数、および散布図3で表される $V^{\prime\prime}$ と $W^{\prime\prime}$ の2種類のデータの相関係数をそれぞれ $r_1$, $r_2$ および $r_3$ とする。これらは、小数第3位を四捨五入して小数第2位まで求めると、 $-0.76$, $0.10$, $0.98$ のいずれかであることがわかっている。
次の $\mybox{タ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つ選べ。
$r_1, r_2$ および $r_3$ の値の組合せとして正しいものは $\myBox{タ}$ である。
$r_1$ $r_2$ $r_3$ 0 $-0.76$ $0.10$ $0.98$ 1 $-0.76$ $0.98$ $0.10$ 2 $0.10$ $-0.76$ $0.98$ 3 $0.10$ $0.98$ $-0.76$ 4 $0.98$ $-0.76$ $0.10$ 5 $0.98$ $0.10$ $-0.76$
解説
散布図1は、 $V$ の平均より大きいときは $W$ の平均より大きい、 $V$ の平均より小さいときは $W$ の平均より小さい、となっているので、強い正の相関があると言えます。
散布図3は、 $V^{\prime\prime}$ の平均より大きいときは $W^{\prime\prime}$ の平均より小さい、 $V^{\prime\prime}$ の平均より小さいときは $W^{\prime\prime}$ の平均より大きい、となっているので、強い負の相関があると言えます。
散布図2の場合は、 $V'$ の平均より大きいときに $W'$ の平均より大きいとも小さいとも言えず、 $V'$ の平均より小さいときも $W'$ の平均より大きいとも小さいとも言えないため、相関があるとは言えません。
以上から、散布図1の相関係数が $0.98$ 、散布図2の相関係数が $0.10$ 、散布図3の相関係数が $-0.76$ と対応することがわかります。
解答
タ:5