【標準】三角関数を含む関数の最大・最小(相互関係利用)
ここでは、三角関数を含む関数の最大・最小を求める問題を考えます。相互関係を利用するものを見ていきます。
三角関数を含む関数の最大・最小
$\theta$ が変わると、 $\cos\theta$ も $\sin\theta$ も両方変化します。2つの異なるものが動くと考えづらいですね。なので、1種類にしたいです。こういうとき、相互関係が使えるのでしたね(参考:【基本】三角関数の相互関係)。
三角関数の相互関係より、 $\cos^2\theta=1-\sin^2\theta$ が成り立ちます。これを使えば、 $y$ を $\sin\theta$ だけで表すことができます。
\begin{eqnarray}
y
&=&
(1-\sin^2\theta)+\sin\theta \\[5pt]
&=&
-\sin^2\theta+\sin\theta+1 \\[5pt]
\end{eqnarray}となります。このまま考えてもいいのですが、 $\sin\theta$ を別の文字で置き換えたほうがわかりやすいですね。
$t=\sin\theta$ とおくことにしましょう。これにより、 $y=-t^2+t+1$ となります。だいぶ考えやすくなりました。しかし、このときに注意しないといけないことがあります。それは、 $t$ の値のとる範囲です。
今、 $0\leqq \theta\lt 2\pi$ の範囲で考えているので、 $t=\sin\theta$ とおいた時点で、 $-1\leqq t\leqq 1$ と、範囲が限定されます。なので、この範囲で $y$ の取りうる値を考えないといけないんですね。こうした内容は、【応用】二次関数の最大・最小(変数置き換え)でも扱っています。
値の取りうる範囲にさえ気をつければ、あとは普通の二次関数の問題として考えていくことができます。
\begin{eqnarray}
y
&=&
-t^2+t+1 \\[5pt]
&=&
-\left(t-\dfrac{1}{2}\right)^2+\dfrac{5}{4} \\[5pt]
\end{eqnarray}となるので、グラフは次のようになります。
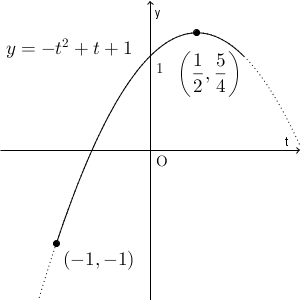
よって、最大となるのは、 $t=\dfrac{1}{2}$ のときです。つまり、 $\sin\theta=\dfrac{1}{2}$ のときなので、 $\theta=\dfrac{1}{6}\pi,\dfrac{5}{6}\pi$ のときです。最大値は $\dfrac{5}{4}$ となります。
最小となるのは、 $t=-1$ のときです。つまり、 $\sin\theta=-1$ のときなので、 $\theta=\dfrac{3}{2}\pi$ であることがわかります。また、最小値は $-1$ です。
まとめると、 $\theta=\dfrac{1}{6}\pi,\dfrac{5}{6}\pi$ のときに最大値 $\dfrac{5}{4}\pi$ をとり、 $\theta=\dfrac{3}{2}\pi$ のときに最小値 $-1$ をとる、というのが答えとなります。
$\theta$ と $y$ の関係を直接見るのは難しいです。しかし、三角関数を別の文字で置き換えることで、わかりやすい二次関数になりました。別の文字で置き換えるときに範囲に注意する必要がありますが、こうした置き換えによって、複雑な関数の最大・最小を求めることができるようになります。
なお、数学IIIを学べば、 $\theta$ と $y$ の関係を直接扱うことも可能となります。例えば、グラフが次のようになる、ということが計算できるようになります。
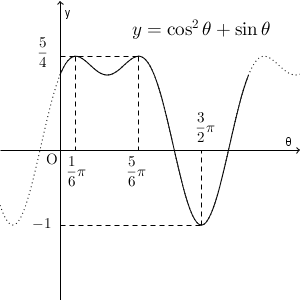
ただ、その方法については、また別の機会に。
おわりに
ここでは、三角関数を含む関数の最大・最小を求める問題を見ました。三角関数を1種類にできる場合は、相互関係を用いて1種類にしてから考えましょう。その際、範囲に注意して考えましょう。





