【標準】一般角の三角関数と鋭角の三角関数

ここでは、 $\dfrac{1}{2}\pi-\theta$ や $\theta+\dfrac{1}{2}\pi$ の三角関数の値について見ていきます。

一般角の三角関数と鋭角の三角関数の復習

【基本】一般角の三角関数と鋭角の三角関数で見た内容を、振り返っておきましょう。

【基本】三角関数の定義で見た通り、 $\mathrm{ O }(0,0)$ を中心に $\mathrm{ A }(1,0)$ を反時計回りに $\theta$ だけ回転したときに、 $\mathrm{ P }(x,y)$ に移るとすると、\[ \sin\theta=y, \cos\theta=x,\tan=\dfrac{y}{x} \]となるのでした（ $x=0$ のとき、 $\tan$ は定義しない）。

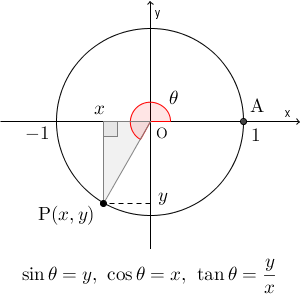
また、一般角の三角関数の値は、もっとわかりやすい角の三角関数の値に変換できるのでしたね。

例えば、 $-\theta$ の三角関数の値を考えるには、 $(1,0)$ を $\theta$ だけ時計回りに回転した点を考えればいいですが、この点と $\theta$ だけ反時計回りに回転した点とを比べると、上下対称であることがわかります。

よって
\begin{eqnarray} \sin(-\theta)&=&-\sin\theta \\[5pt] \cos(-\theta)&=&\cos\theta \\[5pt] \tan(-\theta)&=&-\tan\theta \\[5pt] \end{eqnarray}という関係式が成り立ちます。これにより、マイナスの角はプラスの角に変換できます。

また、時計回りや反時計回りに一周すると同じ点に戻ってくることから、
\begin{eqnarray} \sin(\theta+2n\pi)&=&\sin\theta \\[5pt] \cos(\theta+2n\pi)&=&\cos\theta \\[5pt] \tan(\theta+2n\pi)&=&\tan\theta \end{eqnarray}が成り立ちます（n は整数）。これにより、一般角の三角関数は、 $0$ から $2\pi$ までの三角関数でかけることがわかります。

一周ではなく、半周だけさらに回転した場合は、原点について対称な点に移動するので、
\begin{eqnarray} \sin(\theta+\pi)&=&-\sin\theta \\[5pt] \cos(\theta+\pi)&=&-\cos\theta \\[5pt] \tan(\theta+\pi)&=&\tan\theta \end{eqnarray}が成り立ちます。このことから、 $\pi$ から $2\pi$ までの角を、 $0$ から $\pi$ までの角でかけることがわかります。

最後に、左右対称を考え、 $(-1,0)$ を時計回りに $\theta$ だけ回転した場合を考えましょう。これは、 $(1,0)$ を反時計回りに $\pi-\theta$ だけ回転した点と一致します。また、 $(1,0)$ を $\theta$ だけ回転した点とは y 軸について対称な位置にいます。

このことから、
\begin{eqnarray} \sin(\pi-\theta)&=&\sin\theta \\[5pt] \cos(\pi-\theta)&=&-\cos\theta \\[5pt] \tan(\pi-\theta)&=&-\tan\theta \end{eqnarray}が成り立ちます。これにより、 $0$ から $\dfrac{1}{2}\pi$ までの角でかけることがわかります。

45度以下の角への変換

上で見た内容から、一般角の三角関数は、 $0$ 以上 $\dfrac{1}{2}\pi$ 以下の角の三角関数に変換することができます。これは、さらに、 $\dfrac{1}{4}\pi$ 以下の角に変換することもできます。

$-\theta$ のところで上下対称であることを利用し、 $\pi-\theta$ のところで左右対称であることを利用しました。ここでは、直線 $y=x$ について対称であることを利用して考えていきます。

点 $(0,1)$ を、原点を中心にして、時計回りに $\theta$ だけ回転した点を考えます。これは、点 $(1,0)$ を、反時計回りに回転した場合で考えれば、 $\dfrac{1}{2}\pi-\theta$ だけ回転した点になります。

また、この点は $(1,0)$ を反時計回りに $\theta$ だけ回転した点と比べると $y=x$ について対称なので、 $x$ 座標と $y$ 座標が入れ替わります。また、これにより傾きは逆数になるので、次が成り立ちます。

これは、【基本】余角の三角比で見た内容と見た目は同じですが、一般角に対して成り立つ点が異なります。直線 $y=x$ について対称になることは、一般角に対して成り立ちます。

今までに見た内容を組み合わせると、 $\theta+\dfrac{1}{2}\pi$ の三角関数の値も求められます。例えば、これの $\sin$ の値を考えてみます。$\theta+\pi$ の角、マイナスの角、 $\dfrac{1}{2}\pi-\theta$ の角の関係式を順番に使うと
\begin{eqnarray} \sin \left(\theta+\dfrac{1}{2}\pi\right) &=& -\sin \left(\theta-\dfrac{1}{2}\pi\right) \\[5pt] &=& \sin \left(\dfrac{1}{2}\pi-\theta\right) \\[5pt] &=& \cos \theta \\[5pt] \end{eqnarray}となります。他も同様に変形すると、次が得られます。

これは、図で考えれば、 $(0,1)$ を反時計回りに $\theta$ だけ回転した点に対応します。

この図から座標の対応を考えることもできます。

おわりに

ここでは、一般角の三角関数をよりわかりやすい角に変換する方法を見てきました。 $\dfrac{1}{2}\pi-\theta$ や $\theta+\dfrac{1}{2}\pi$ について見てきました。公式を忘れても、図をかいて対応を思い出せるようにしておきましょう。