【標準】複素数平面と直線に対する対称移動

🕒 2019/02/19 🔄 2023/05/01

ここでは、複素数平面で、実軸以外の直線に関する対称移動について見ていきます。

📘 目次

実軸以外の直線に関する対称移動

例題

直線 $y=2x$ に関して、点 $\mathrm{ P }(2+i)$ と対称な点を $\mathrm{ Q }(w)$ とするとき、複素数 $w$ を求めなさい。

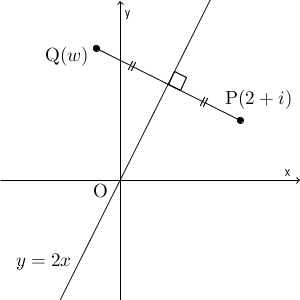
複素数平面での対称移動は、【基本】複素数平面と共役複素数で登場しました。実軸に関して、点 $\alpha$ と対称な点は、 $\overline{\alpha}$ と書けるのでした。虚部の符号を変えるだけなので、共役複素数で表せるのでしたね。

しかし、この例題では、実軸ではなく、別の直線に関する対称移動となっています。そのため、共役複素数をそのまま使うことはできません。どうすればいいでしょうか。

「実軸じゃないから使えない」のだから、無理やり「実軸に関する対称移動」が使える形にしてみましょう。つまり、直線 $y=2x$ が実軸と重なるように、全体を回転させてから考えればいいわけですね。そして、実軸に関する対称移動を行ってから、元に戻すように回転させる、という流れです。回転も対称移動も、複素数の演算で書けるので、これで答えにたどりつけそうですね。

ではまず、どのように回転すればいいかを考えましょう。直線 $y=2x$ と実軸の正の向きとのなす角を $\theta$ とします。ここで、 $0\lt\theta\lt\dfrac{\pi}{2}$ となるようにとります。三角関数の相互関係も使うと
\begin{eqnarray} \tan\theta &=& 2 \\[5pt] \cos\theta &=& \frac{1}{\sqrt{5} } \\[5pt] \sin\theta &=& \frac{2}{\sqrt{5} } \\[5pt] \end{eqnarray}となることがわかります。この $\theta$ を使って\[ \alpha=\cos\theta+i\sin\theta \]と置くと、次の3ステップで計算していくことになります。

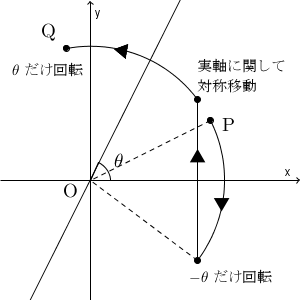
はじめに、 $\dfrac{1}{\alpha}$ を掛けます。これは、直線 $y=2x$ が実軸と重なるように回転移動することに対応しています。

次に、共役複素数を考えます。これは、実軸に関する対称移動に対応しています。

最後に、 $\alpha$ を掛ければ、実軸が直線 $y=2x$ と重なるように回転移動することになります。

これらをまとめると、求めたい複素数 $w$ が出てくるわけですね。式で書くと次のようになります。
\begin{eqnarray} w &=& \overline{\left\{(2+i)\times\dfrac{1}{\alpha}\right\} }\times\alpha \\[5pt] &=& \dfrac{\overline{2+i} }{\overline{\alpha} }\times\alpha \\[5pt] \end{eqnarray}ここで、【基本】複素数平面と絶対値で見た通り、 $\alpha\overline{\alpha}=|\alpha|^2$ であり、今、 $|\alpha|=1$ なので、 \begin{eqnarray} w&=& \dfrac{\overline{2+i} }{\overline{\alpha} }\times\alpha \\[5pt] &=& (2-i)\alpha^2 \\[5pt] &=& (2-i)(\cos2\theta+i\sin2\theta) \\[5pt] \end{eqnarray}となります。倍角の公式から \begin{eqnarray} \cos2\theta &=& 2\cos^2\theta-1=\frac{2}{5}-1=-\frac{3}{5} \\[5pt] \sin2\theta &=& 2\sin\theta\cos\theta=\frac{4}{5} \\[5pt] \end{eqnarray}なので、 \begin{eqnarray} w&=& (2-i)(\cos2\theta+i\sin2\theta) \\[5pt] &=& (2-i)\times\frac{-3+4i}{5} \\[5pt] &=& \frac{(-6+4)+(8+3)i}{5} \\[5pt] &=& \frac{-2+11i}{5} \\[5pt] \end{eqnarray}となります。これが答えです。

一般の場合

すごく複雑なことをしているように見えるかもしれませんが、式で書くとそれほど難しくはありません。一般的な状況で、式を書いてみましょう。

直線 $y=mx$ に関して、点 $\mathrm{ P }(z)$ と点 $\mathrm{Q}(w)$ が対称であったとしましょう。このとき、この直線と実軸の正の向きとのなす角を $\theta$ とし（反時計回りが正の方向）、 $\alpha=\cos\theta+i\sin\theta$ としましょう。

このとき、先ほど見たように、(1)対称の軸が実軸に来るように回転する、(2)実軸に関して対称移動する、(3)実軸をもとの対称の軸に戻るように回転する、という手順で考えます。

これを式で書けば、
\begin{eqnarray} w &=& \overline{\left\{z\times\dfrac{1}{\alpha}\right\} }\times\alpha \\[5pt] &=& \dfrac{\overline{z} }{\overline{\alpha} }\times\alpha \\[5pt] &=& \overline{z}\alpha^2 \\[5pt] \end{eqnarray}となります。具体的に計算すると、先ほどの例題のように計算量は少し増えますが、実際には\[ \overline{z}\alpha^2 \]を計算しているだけです。実軸に関する対称移動の場合は、 $\alpha=1$ のときに対応するので、共役複素数になることが確かめられます。

この式は公式として覚えておく必要はありませんが、結果だけを見ればシンプルですね。