【応用】三角関数のグラフ

🕒 2018/05/03 🔄 2023/05/01

ここでは、三角関数のグラフのかき方や、グラフを用いて等式や不等式の問題に応用する方法を考えていきます。

📘 目次

三角関数のグラフ

【標準】三角関数のグラフで見た内容を組み合わせて、\[ y=\cos\left(2\theta-\dfrac{1}{4}\pi\right) \]のグラフを考えてみましょう。

まず、 $2\theta$ の部分から考えてみましょう。\[ y=\cos 2\theta \] のグラフは、 $y=\cos\theta$ のグラフを $\theta$ 軸方向に $\dfrac{1}{2}$ 倍したものになります。

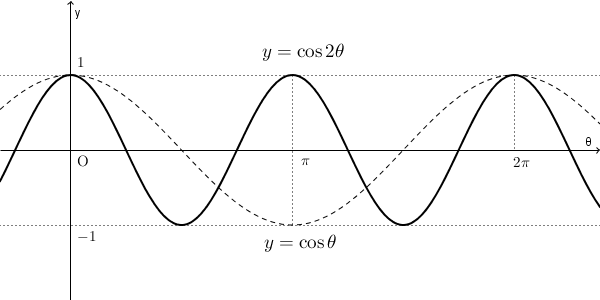
これをもとに、\[ y=\cos\left(2\theta-\dfrac{1}{4}\pi\right) \]のグラフを考えてみましょう。上で見たグラフを、 $\theta$ 方向に $\dfrac{1}{4}\pi$ だけ平行移動すればいいとやってしまいがちですが、そうではありません。例えば、 $y=1$ になるときの $\theta$ を考えてみましょう。平行移動する前は $\theta=0$ であり、平行移動した後は $\theta=\dfrac{1}{8}\pi$ になります。 $\dfrac{1}{4}\pi$ だけ平行移動するのは間違いです。

このような間違いをしないために、平行移動について考える前に、次のように式変形をしましょう。\[ y=\cos\left\{2\left(\theta-\dfrac{1}{8}\pi\right)\right\} \]正しくは、 $\dfrac{1}{8}\pi$ だけ平行移動する、です。グラフは次のようになります。

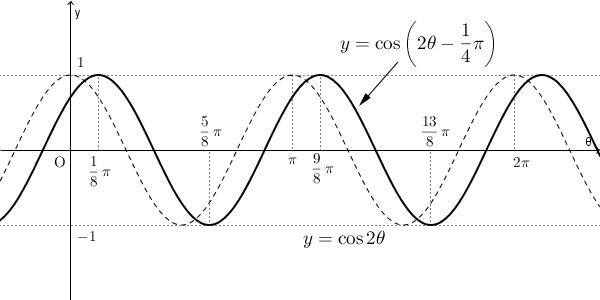
【発展】グラフの平行移動でも見たことからもわかる通り、 $\theta$ 方向に $\dfrac{1}{8}\pi$ だけ平行移動すると、対応する関数は $\theta$ の部分が $\theta-\dfrac{1}{8}\pi$ に変わります。よって、 $y=\cos 2\theta$ のグラフは、 $y=\cos\left\{2\left(\theta-\dfrac{1}{8}\pi\right)\right\}$ のグラフに移動することになります。

平行移動の部分から考えるには、 $\theta$ 方向に $\dfrac{1}{4}\pi$ だけ平行移動し、 $\theta$ 軸方向に $\dfrac{1}{2}$ 倍する、という順番になります。平行移動後のグラフは $y=\cos\left(\theta-\dfrac{1}{4}\pi\right)$ のグラフとなります。縮小後は、 $\theta$ が $2\theta$ に変わって、\[ y=\cos\left(2\theta-\dfrac{1}{4}\pi\right) \]のグラフが得られます。

もちろん、どちらから考えても同じ結果になります。

三角関数のグラフを等式・不等式の問題に応用する

【応用】三角関数を含む等式・不等式（変域が変わる）では、三角関数を含む等式や不等式を解くときに、単位円を使って考えました。単位円を用いるのが普通ですが、三角関数のグラフを利用する方法もあります。

例えば、 $0\leqq \theta\lt 2\pi$ の範囲で\[ \cos\left(2\theta-\dfrac{1}{4}\pi\right)\gt \dfrac{1}{2} \]を解いてみましょう。これは、上のリンク先の後半と同じ問題です。

\[ y=\cos\left(2\theta-\dfrac{1}{4}\pi\right) \]のグラフは、先ほど見た通りです。これと $y=\dfrac{1}{2}$ とのグラフとを比較して、該当する範囲は次の赤線部分のようになることがわかります。

以上から、 $0\leqq \theta\lt\dfrac{7}{24}\pi$, $\dfrac{23}{24}\pi\lt \theta\lt\dfrac{31}{24}\pi$, $\dfrac{47}{24}\pi\lt \theta\lt 2\pi$ が求める範囲となります。

グラフをかいて考えると、いくつか答えがある場合に漏れることが少ないかもしれません。ただ、グラフをかくこと自体に時間がかかってしまうこと、正確なグラフをかくことが難しいことから、あまり推奨はできません。グラフを使って考えることもできる、ということを頭の片隅に入れておく程度でいいでしょう。時間があるときの検算として使ってもいいかもしれません。