【応用】三角関数を含む方程式の解の個数

ここでは、三角関数を含む方程式の解の個数を調べる問題を考えます。

三角関数を含む方程式の解の個数

問題文にある「 $a$ を定数とする」とは、 $\theta$ とは関係ない数だ、ということです。問題文にある方程式は、 $a$ の値によって、解の個数が変わってきます。 $\sin$ も $\cos$ も値の絶対値は $1$ 以下なのだから、極端な話でいうと $a=10$ のときには解はありません。でも、例えば $a=1$ なら、 $\theta=\dfrac{1}{2}\pi$ という解がありますね。つまり、解の個数は、 $a$ の値によって場合分けをして答えることになります。

方程式を直接見ていても難しいので、グラフを使いましょう。まず、 $y=\cos^2\theta+\sin\theta-a$ と $\theta$ 軸との共有点の数に注目する案が考えられます。ただ、これだと $a$ が変わるごとにグラフが上下してわかりづらいですね。これよりも、 $y=\cos^2\theta+\sin\theta$ と $y=a$ との共有点の数に注目したほうがわかりやすいです。直線 $y=a$ の方を上下したほうが考えやすいですね。

続いて、 $y=\cos^2\theta+\sin\theta$ のグラフを考えましょう。これをそのまま扱うのは難しいですが、【標準】三角関数を含む関数の最大・最小（相互関係利用）で見たように、 $\sin\theta=t$ とおくと考えやすくなります。相互関係を使うと
\begin{eqnarray} & & \cos^2\theta+\sin\theta \\[5pt] &=& (1-\sin^2\theta)+\sin\theta \\[5pt] &=& -t^2+t+1 \\[5pt] \end{eqnarray}となります。

以上のことを用いて、まずは、 $y=-t^2+t+1$ と $y=a$ との共有点の数を考えます。次に、そのときの $t$ の値に対して、 $\sin\theta=t$ を満たす $\theta$ を数える、という方針で考えていきます。

ただ、いくつか注意点があります。1つは、 $t$ の範囲です。上のリンク先でも見ましたが、 $-1\leqq t \leqq 1$ の範囲で考えないといけない、という点には注意しないといけません。

また、 $\sin\theta=t$ をみたす $\theta$ の数は、 $t$ の値によって変わることにも注意が必要です。 $0\leqq \theta\lt 2\pi$ の範囲では、 $t\ne\pm1$ のときは解が2つありますが、 $t=1$ のときも、 $t=-1$ のときも、解は1つです。

以上を踏まえて考えていきます。まず、 $-1\leqq t \leqq 1$ の範囲で $y=-t^2+t+1$ のグラフは次のようになります。

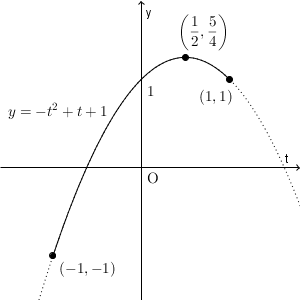
これと $y=a$ との共有点を考えましょう。共有点が存在するのは、 $-1\leqq a\leqq \dfrac{5}{4}$ のときですね。これ以外の場合は、共有点が存在しないので、方程式の解も存在しません。

続いて、 $a$ の値が小さい場合から考えていきましょう。まず、 $a=-1$ のときです。

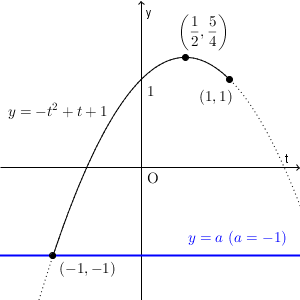
このとき、共有点の $t$ 座標は $-1$ です。 $\sin\theta=-1$ を満たす $\theta$ は1個なので、この場合の解の個数は1個となります。

次に、 $-1\lt a\lt 1$ の場合を考えます。

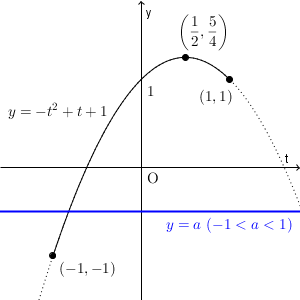
このとき、共有点は1つで、その $t$ 座標は $-1$ と $1$ の間です（両端を除く）。よって、 $\sin\theta=t$ を満たす $\theta$ は2個となり、解の個数も2個となります。

また、 $a=1$ のときは、次のようになります。

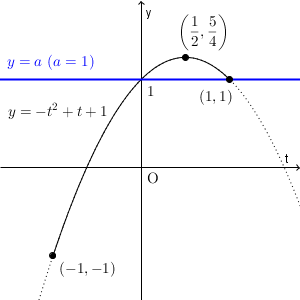
このとき、共有点は2つです。 $t$ 座標については、片方は $1$ 、もう片方は $-1$ と $1$ の間です（両端を除く）。前者について、 $\sin\theta=t$ を満たす $\theta$ は1個で、後者については2個なので、解の個数は3個となります。

続いて、 $1\lt a\lt \dfrac{5}{4}$ のときを考えます。

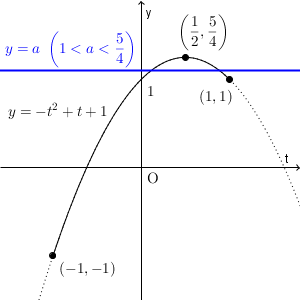
共有点は2つですが、どちらの $t$ 座標も、 $-1$ と $1$ の間です（両端を除く）。 $\sin\theta=t$ を満たす $\theta$ は2個ずつなので、解の個数は4個となります。

最後に、 $a=\dfrac{5}{4}$ の場合を考えましょう。

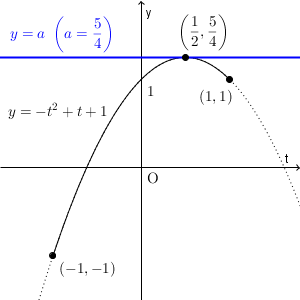
この場合、共有点の数は1個で、そのときの t 座標は $\dfrac{1}{2}$ です。このとき、 $\sin\theta=t$ を満たす $\theta$ は2個なので、方程式の解の個数は2個です。

以上から、次が答えとなります。

　$a\lt -1$ のときは0個、
　$a=-1$ のときは1個、
　$-1\lt a\lt 1$ のときは2個、
　$a=1$ のときは3個、
　$1\lt a\lt \dfrac{5}{4}$ のときは4個、
　$a=\dfrac{5}{4}$ のときは2個、
　$a\gt \dfrac{5}{4}$ のときは0個

場合分けが大変ですが、場合分けができれば、あとはそれほど難しくはないでしょう。 $t=\pm1$ のときの扱いを間違えないように注意しましょう。

おわりに

ここでは、三角関数を含む方程式の解の個数を考える問題を見ました。定数によって解の個数を答える問題でしたが、問題によっては、「解の個数が2個の場合の定数の範囲を求めなさい」などと言われる場合もあります。考え方はここでの例題と同じです。 $\sin\theta=t$ などと置いた場合、 $t$ の個数、そして、そのときの $\theta$ の個数を、順番に考えていきましょう。