【基本】一般角の三角関数と鋭角の三角関数

ここでは、一般角の三角関数を鋭角の三角関数に変換していく方法について見ていきます。

三角関数の復習

【基本】三角関数の定義で見た通り、 $\mathrm{ O }(0,0)$ を中心に $\mathrm{ A }(1,0)$ を反時計回りに $\theta$ だけ回転したときに、 $\mathrm{ P }(x,y)$ に移るとすると、\[ \sin\theta=y, \cos\theta=x,\tan=\dfrac{y}{x} \]となるのでした（ $x=0$ のとき、 $\tan$ は定義しない）。

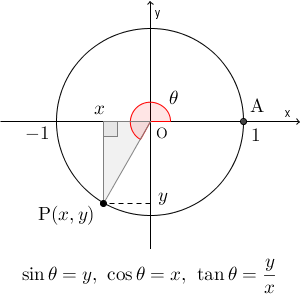
これにより、いろんな角に対して三角関数を定義することができるようになりましたが、より考えやすい角の三角関数に変換することができます。以下で、その方法を見ていきましょう。

なお、以下で出てくる角度は弧度法を使っているので、わからない人は【基本】弧度法を見ましょう。

マイナス角の三角関数

まず、マイナスの角の三角関数について考えましょう。例えば、 $-\dfrac{2}{3}\pi$ の場合、 $(1,0)$ を時計回りに $\dfrac{2}{3}\pi$ だけ回転して移る点を考えることになります。

これは、反時計回りを考えるときと、上下対称になります。つまり、反時計回りに $\dfrac{2}{3}\pi$ だけ回転した点と比べると、 x 座標はそのまま、 y 座標は $-1$ 倍、よって、傾きは $-1$ 倍、となることがわかります。

これは、他の角度に対しても同様です。上下対称になることから、次の関係が成り立ちます。

この変換を使えば、マイナスの角の三角関数は、プラスの角の三角関数に変換することができます。例えば、 $\sin\left(-\dfrac{11}{3}\pi\right)=-\sin\dfrac{11}{3}\pi$ などとなります。

一周以上する角の三角関数

次は、一周以上する角の場合、例えば、 $\dfrac{10}{3}\pi$ の三角関数を考えてみましょう。ちなみに、一周は $2\pi$ ですね。

一周すると同じ点に戻ってくることから、一周する前とした後では、 x 座標も y 座標も同じで、もちろん傾きも同じになります。

よって、次が成り立ちます。

これにより、 $2\pi$ より大きい角の三角関数は、 $2\pi$ 以下の角の三角関数に変換できることがわかります。例えば、 $\cos\dfrac{11}{3}\pi=\cos\dfrac{5}{3}\pi$ などとなります。

半周以上する角の三角関数

続いて、半周以上、つまり、 $\pi$ 以上の場合を考えてみます。

原点を中心に点を回転させる場合、半周だけさらに回転させれば、原点について点対称な点に移動します。

このことから、 $\pi$ だけさらに回転させると、 $x$ 座標も $y$ 座標も $-1$ 倍され、傾きは変わらない、となります。よって、次が成り立ちます。

これにより、 $\pi$ より大きい角の三角関数を、 $\pi$ 以下の角の三角関数に変換できることがわかります。例えば、 $\cos\dfrac{5}{3}\pi=-\cos\dfrac{2}{3}\pi$ などとなります。

直角以上の角の三角関数

最後に、直角以上の角の場合を考えてみます。

マイナスの角のときには、上下対称で考えましたが、今回は、左右対称で考えてみましょう。つまり、 $(-1,0)$ を、時計回りに $\theta$ だけ回転した場合と比較して考えてみます。このとき、 $(1,0)$ を反時計回りに $\pi-\theta$ だけ回転したことと同じになります。

また、 $(1,0)$ を反時計回りに $\theta$ だけ回転した場合と座標はどうなるでしょうか。左右対称となるので、 x 座標は $-1$ 倍で、 y 座標は変わりません。傾きは $-1$ 倍となるので、次が成り立ちます。

例えば、 $\cos\dfrac{2}{3}\pi=-\cos\dfrac{1}{3}\pi$ などとなります。これにより、 $\dfrac{1}{2}\pi$ より大きい角の三角関数を、 $\dfrac{1}{2}\pi$ 以下の角の三角関数に変換できることがわかります。この式は、補角の公式として【基本】補角の三角比でも出てきていますが、ここでは、一般角に対して成り立つ、ということが新しい内容になっています。

おわりに

ここでは、一般角の三角関数を、より分かりやすい角の三角関数に変換できることを見ました。まず、マイナスの角の場合は、プラスの角の三角関数で表現でき、 $2\pi$ より大きい場合は $2\pi$ 以下の角で表現でき、さらに $\pi$ 以下で表現でき、最終的には、 $0$ から $\dfrac{1}{2}\pi$ までの角の三角関数を使って表せることができる、ということがわかりました。わかりにくい角度は、小さい角に変換してから考えるようにしましょう。