【基本】三角関数の定義

ここでは、一般角に対する三角関数について見ていきます。

三角比の復習

【基本】三角比の定義（直角三角形による定義）で見た通り、もともと、 $\sin$, $\cos$, $\tan$ は、直角三角形の辺の長さを使って定義していましたね。

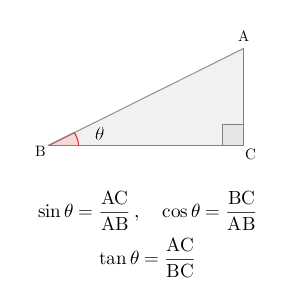
これにより、鋭角に対して三角比を定義することができますが、鈍角に対しては、定義することができません。

そこで、【基本】鈍角の三角比で見たように、円を使って定義するのでしたね。

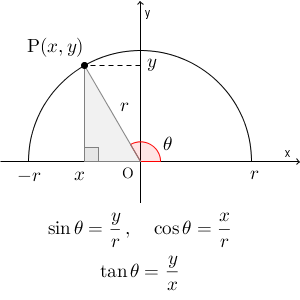
言葉で書くと、まず、原点を中心とした半径 r の円をかきます。 $\mathrm{ O }(0,0)$ を中心に $\mathrm{ A }(r,0)$を $\theta$ だけ反時計回りに回転して移動する点を $\mathrm{ P }(x,y)$ としたとき、三角比を\[ \sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x} \]と定義する、ということです（ただし、 $\tan90^{\circ}$ は定義できない）。

この円を使った定義では、鋭角の部分では、直角三角形を使った定義と同じものになります。この手法により、 $0^{\circ}\leqq \theta\leqq 180^{\circ}$ の場合に、三角比を拡張して定義することができるようになるのでした。

一般角

さて、三角比について振り返ってみましたが、円を使った定義では、別に0度から180度までに限る必要はない、ということがわかるでしょう。180度より回転してもいいし、時計回りに回転してもいいですね。

角度を回転として考えれば、回転の向きと大きさによって、負の角や360度より大きい角も考えられます。このようにして拡張した角を、一般角といいます。

回転として考えるなら、基準と動くもののの2つが必要ですね。基準となる線（半直線）を始線といい、動くもの（半直線）を動径といいます。

一般角に対する三角関数

円を使った三角比の定義を使えば、一般角に対しても、同じように定義できます。

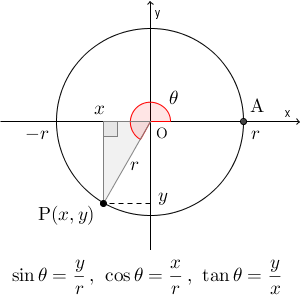
$\mathrm{ O }(0,0)$ を中心に $\mathrm{ A }(r,0)$を $\theta$ だけ反時計回りに回転して移動する点を $\mathrm{ P }(x,y)$ としたとき、三角比を\[ \sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x} \]と定義します（ただし、 $x=0$ のときは $\tan$ は定義しない）。これは、 r の値によって変わることはありません（相似になるから）。この定義の仕方は、0度から180度までのときと同じです。なので、定義できる角度の範囲が広がった、ということです。

例えば、 $\theta=240^{\circ}$ の場合を考えてみましょう。

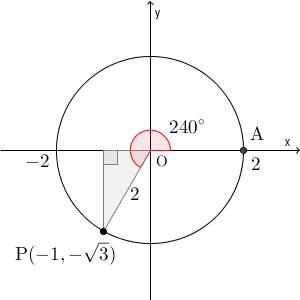
図より、 $\sin 240^{\circ}=-\dfrac{\sqrt{3} }{2}$, $\cos 240^{\circ}=-\dfrac{1}{2}$, $\tan 240^{\circ}=\sqrt{3}$ となります。180度までのときとは異なり、 $\sin$ が負になることもあります。

360度より大きい場合も考えることができます。例えば、 $\theta=600^{\circ}$ の場合を考えると、1周と $240^{\circ}$ なので、 $240^{\circ}$ と同じ値になることがわかります。

数学の世界では、反時計回りを正の向きとして扱います。時計回りは負の向きです。なので、例えば、 $\theta=-120^{\circ}$ というのは、先ほどの $\theta=240^{\circ}$ のときと同じ値になります。

こうして、どんな角に対しても、 $\sin$, $\cos$, $\tan$ を定義することができるようになりました。これらは、角度を決めれば値が1つに決まる、つまり、角度についての関数です。そのため、これらを三角関数(trigonometric functions) と呼びます。

もともとこれらは三角比と呼んでいて、三角形の辺の長さや角の大きさを調べるのに使っていました。今後はまた違った使い方をしていくため、見た目は同じですが、名前を変えて扱っていくことになります。

単位円

さて、円を使って三角関数を定義しましたが、そもそも半径は r でなくてもいいですね。 $\sin$ も $\cos$ も r で割ることになるので、はじめから半径が $1$ の場合で考える方が楽です。

原点を中心とし、半径が $1$ の円のことを単位円といいます。単位円上で考えれば、三角関数は次のように定義できます。\[ \sin\theta=y,\cos\theta=x,\tan\theta=\frac{y}{x} \]

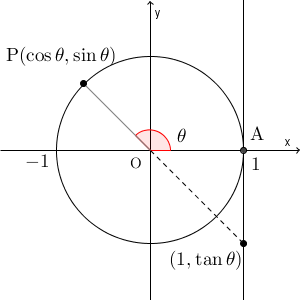
このことから、 $\sin\theta$, $\cos\theta$ は $-1$ 以上 $1$ 以下の値をとることがわかります。また、 $\tan\theta$ は、直線 OP の傾きであり、 $x=1$ のときの y 座標だから、すべての実数値をとることもわかります。

おわりに

ここでは、一般角に対する三角関数の定義について見てきました。鈍角の三角比の定義を利用して、定義することができました。 $\sin$ が負になることがあるなど、今まで見慣れない性質も出てきますが、慣れていくようにしましょう。