共通テスト 数学II・数学B 2018年度プレテスト 第1問 [1] 解説
2018年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
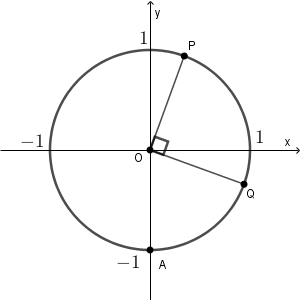
O を原点とする座標平面上に、点 $\mathrm{A}(0,-1)$ と、中心が O で半径が $1$ の円 $C$ がある。円 $C$ 上に $y$ 座標が正である点 P をとり、線分 OP と $x$ 軸の正の部分とのなす角を $\theta\ (0\lt \theta\lt \pi)$ とする。また、円 $C$ 上に $x$ 座標が正である点 Q を、つねに $\angle \mathrm{POQ}=\dfrac{\pi}{2}$ となるようにとる。次の問いに答えよ。
(1) P, Q の座標をそれぞれ $\theta$ を用いて表すと
\begin{eqnarray} \mathrm{P} \left(\myBox{ア}, \myBox{イ}\right) \\[5pt] \mathrm{Q} \left(\myBox{ウ}, \myBox{エ}\right) \\[5pt] \end{eqnarray}である。 $\myBox{ア}$ ~ $\myBox{エ}$ に当てはまるものを、次の 0 ~ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。0: $\sin\theta$
1: $\cos\theta$
2: $\tan\theta$
3: $-\sin\theta$
4: $-\cos\theta$
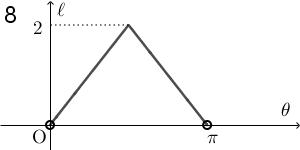
5: $-\tan\theta$(2) $\theta$ は $0\lt \theta\lt \pi$ の範囲を動くものとする。このとき線分 AQ の長さ $\ell$ は $\theta$ の関数である。関数 $\ell$ のグラフとして最も適当なものを、次の 0 ~ 9 のうちから一つ選べ。 $\myBox{オ}$
考え方
(2)は、選択肢がたくさんあってめんどくさそうですが、明らかに間違っているものがたくさんあるので、そんなに大変ではありません。計算だけで選択肢を選ぶのは少し大変ですが、選択肢から選ぶだけなら、特別なケースから消去していって解くこともできます。
解答編
問題
O を原点とする座標平面上に、点 $\mathrm{A}(0,-1)$ と、中心が O で半径が $1$ の円 $C$ がある。円 $C$ 上に $y$ 座標が正である点 P をとり、線分 OP と $x$ 軸の正の部分とのなす角を $\theta\ (0\lt \theta\lt \pi)$ とする。また、円 $C$ 上に $x$ 座標が正である点 Q を、つねに $\angle \mathrm{POQ}=\dfrac{\pi}{2}$ となるようにとる。次の問いに答えよ。
(1) P, Q の座標をそれぞれ $\theta$ を用いて表すと
\begin{eqnarray} \mathrm{P} \left(\myBox{ア}, \myBox{イ}\right) \\[5pt] \mathrm{Q} \left(\myBox{ウ}, \myBox{エ}\right) \\[5pt] \end{eqnarray}である。 $\myBox{ア}$ ~ $\myBox{エ}$ に当てはまるものを、次の 0 ~ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。0: $\sin\theta$
1: $\cos\theta$
2: $\tan\theta$
3: $-\sin\theta$
4: $-\cos\theta$
5: $-\tan\theta$
解説
$\theta$ の場所は下の図の通りです。
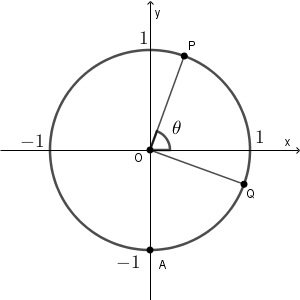
P の座標は、 $(\cos\theta,\sin\theta)$ です。 Q の座標は $\left( \cos\left(\theta-\dfrac{\pi}{2}\right), \sin\left(\theta-\dfrac{\pi}{2}\right) \right)$ です。また、
\begin{eqnarray}
\cos\left(\theta-\dfrac{\pi}{2}\right) &=& \sin\theta \\[5pt]
\sin\left(\theta-\dfrac{\pi}{2}\right) &=& -\cos\theta \\[5pt]
\end{eqnarray}が成り立ちます。これは図で考えてもいいですし、加法定理を使って考えてもいいです。

これより、 Q の座標は $(\sin\theta,-\cos\theta)$ と書けることがわかります。
なお、選択肢から答えを選ぶだけなら、 $\theta=\dfrac{\pi}{6}$ のときなど、特別な値を代入して考えることもできます。
解答
アイウエ:1004
解答編 つづき
問題
(2) $\theta$ は $0\lt \theta\lt \pi$ の範囲を動くものとする。このとき線分 AQ の長さ $\ell$ は $\theta$ の関数である。関数 $\ell$ のグラフとして最も適当なものを、次の 0 ~ 9 のうちから一つ選べ。 $\myBox{オ}$
解説
点 P, Q は次のように動きます。( $\theta=0,\pi$ のときも含めています)
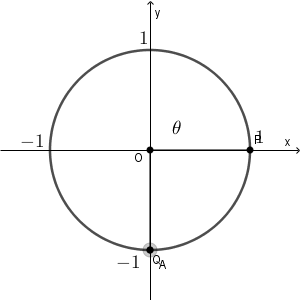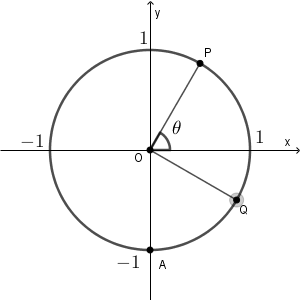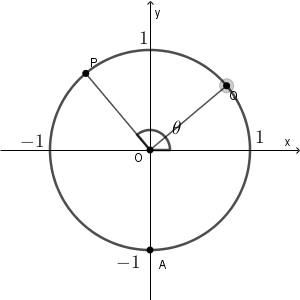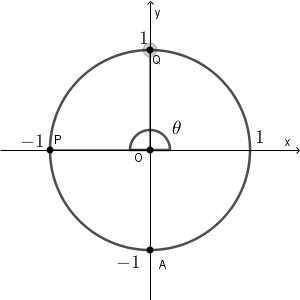
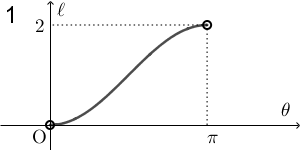
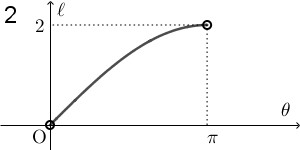
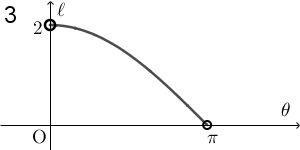
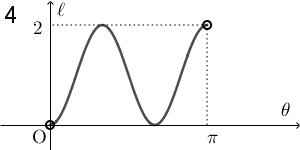
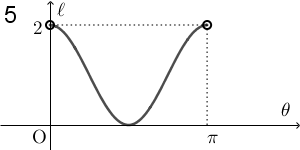
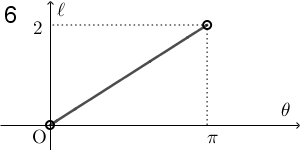
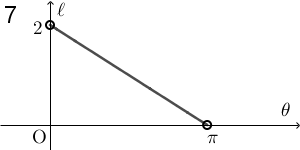
$\theta$ が $0$ に近いところでは AQ の長さは $0$ に近く、 $\pi$ に近いところでは $2$ に近いことがわかります。また、長さが $0$ になることはありません。この時点で、1, 2, 6 以外の選択肢は消えます。
$\theta=\dfrac{\pi}{2}$ のときに AQ の長さは $\sqrt{2}$ ですが、残っている選択肢の中で、 1 と 6 は、 $\theta=\dfrac{\pi}{2}$ のときに $\ell=1$ となっているので、これらも誤りです。なので、2 が正解だとわかります。
また、計算で求めることもできます。 A, Q の座標がわかっているので、
\begin{eqnarray}
\mathrm{ AQ }
&=&
\sqrt{\sin^2\theta+\{-\cos\theta-(-1)\}^2} \\[5pt]
&=&
\sqrt{\sin^2\theta+\cos^2\theta-2\cos\theta+1} \\[5pt]
&=&
\sqrt{2-2\cos\theta} \\[5pt]
&=&
\sqrt{2\cdot 2\sin^2\dfrac{\theta}{2} } \\[5pt]
&=&
2\sin\dfrac{\theta}{2} \\[5pt]
\end{eqnarray}と計算できます。途中で、半角の公式(参考:【標準】半角の公式)を用いています。また、 $0\lt\theta\lt\pi$ の範囲で $\sin\dfrac{\theta}{2}$ が正であることも使っています。
このグラフにあうものは選択肢 2 なので、こうして 2 を選ぶこともできます。
解答
オ:2