共通テスト 数学II・数学B 2017年度プレテスト 第1問 [3] 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
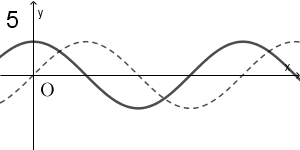
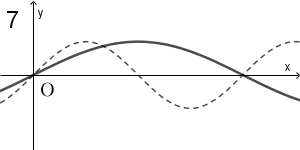
(1) 下の図の点線は $y=\sin x$ のグラフである。(i)、(ii)の三角関数のグラフが実線で正しくかかれているものを、下の 0 ~ 9 のうちから1つずつ選べ。ただし、同じものを選んでもよい。
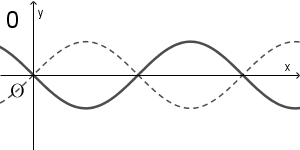
(i) $y=\sin 2x$ $\myBox{ケ}$
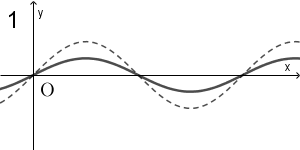
(ii) $y=\sin \left(x+\dfrac{3}{2}\pi\right)$ $\myBox{コ}$
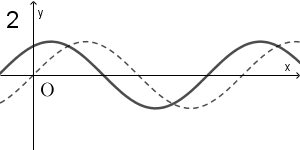
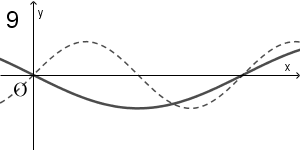
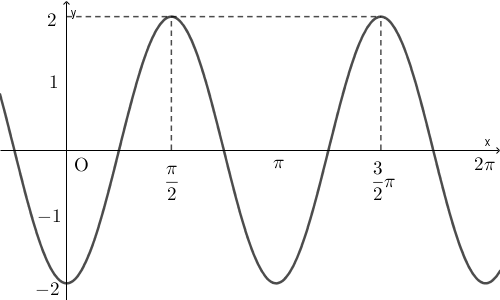
(2) 次の図はある三角関数のグラフである。その関数の式として正しいものを、下の 0 ~ 7 のうちからすべて選べ。 $\myBox{サ}$
0: $y=2\sin\left(2x +\dfrac{\pi}{2}\right)$
1: $y=2\sin\left(2x -\dfrac{\pi}{2}\right)$
2: $y=2\sin 2\left(x +\dfrac{\pi}{2}\right)$
3: $y=\sin2\left(2x -\dfrac{\pi}{2}\right)$
4: $y=2\cos\left(2x +\dfrac{\pi}{2}\right)$
5: $y=2\cos 2\left(x -\dfrac{\pi}{2}\right)$
6: $y=2\cos 2\left(x +\dfrac{\pi}{2}\right)$
7: $y=\cos2\left(2x -\dfrac{\pi}{2}\right)$
考え方
三角関数のグラフに関する問題で、センター試験ではあまり見られなかった問題です。
選択肢が多いですが、あきらかに違っているものを消去して考えるようにすると解きやすくなります。
【必答問題】
解答編
問題
(1) 下の図の点線は $y=\sin x$ のグラフである。(i)、(ii)の三角関数のグラフが実線で正しくかかれているものを、下の 0 ~ 9 のうちから1つずつ選べ。ただし、同じものを選んでもよい。
(i) $y=\sin 2x$ $\myBox{ケ}$
(ii) $y=\sin \left(x+\dfrac{3}{2}\pi\right)$ $\myBox{コ}$
解説
点線のグラフが $y=\sin x$ のグラフであることから、 $(\pi,0)$ や $(2\pi,0)$ の点がわかります。
(i) の $y=\sin 2x$ について考えます。いくつかの値を確認して、候補をしぼっていきましょう。
まず、 $x=0$ のときは $y=0$ です。このことから、2, 5, 6 が候補から外れます。 $x=\pi$ のときも $y=0$ なので、点線のグラフが $x$ 軸と交わっているとき、実線のグラフも $x$ 軸で交わっていないといけません。このことから、7, 8, 9 が候補から外れます。
残っているものは、0, 1, 3, 4 の4つです。 $\sin x$ は $x$ が $0$ より大きい値をとるとき、しばらくは正の値をとるので、0 のようなグラフになることはありません。また、 $y=\sin 2x$ の最大値は $1$ なので、1 や 3 のようなグラフになることもありません。
こうして、4が正解だとわかります。
$y=\sin 2x$ は、 $x$ 軸といつ交わるかを考えると、 $x=\dfrac{\pi}{2}, \pi, \dfrac{3}{2}\pi$ などのときなので、このことから4を選ぶこともできます。
(ii) の $y=\sin \left(x+\dfrac{3}{2}\pi\right)$ について考えましょう。
$x=0$ のときは $y=-1$ なので、候補は 6 だけです。なので、これが答えです。
$y=\sin \left(x+\dfrac{3}{2}\pi\right)=\sin \left\{x-\left(-\dfrac{3}{2}\pi\right)\right\}$ なので、このグラフは $y=\sin x$ のグラフを $x$ 軸方向に $-\dfrac{3}{2}$ だけ平行移動したものになります。このことからも、6が正解だとわかります。
解答
ケコ:46
参考
解答編 つづき
問題
(2) 次の図はある三角関数のグラフである。その関数の式として正しいものを、下の 0 ~ 7 のうちからすべて選べ。 $\myBox{サ}$
0: $y=2\sin\left(2x +\dfrac{\pi}{2}\right)$
1: $y=2\sin\left(2x -\dfrac{\pi}{2}\right)$
2: $y=2\sin 2\left(x +\dfrac{\pi}{2}\right)$
3: $y=\sin2\left(2x -\dfrac{\pi}{2}\right)$
4: $y=2\cos\left(2x +\dfrac{\pi}{2}\right)$
5: $y=2\cos 2\left(x -\dfrac{\pi}{2}\right)$
6: $y=2\cos 2\left(x +\dfrac{\pi}{2}\right)$
7: $y=\cos2\left(2x -\dfrac{\pi}{2}\right)$
解説
グラフからわかることをもとに、候補をしぼっていきましょう。
$x=0$ のとき、 $y=-2$ です。それぞれの選択肢で $x=0$ としたときの $y$ の値は
0: $2$
1: $-2$
2: $0$
3: $0$
4: $0$
5: $-2$
6: $-2$
7: $-1$
なので、この時点で、候補は 1, 5, 6 にしぼられます。
これらの候補は、 $\sin$ や $\cos$ の前に $2$ があり、最大値が $2$ であることと整合的です(これは、縦の幅のチェックに対応しています)。
また、 $\sin$ や $\cos$ の内側の $x$ の係数が $2$ なので、周期は $\pi$ となり、グラフの内容と整合的です(これは、横の幅のチェックに対応しています)。
式から $x=0$ のときに最小値をとり、 $x=\dfrac{\pi}{2}$ のときに最大値をとることがわかるので、グラフの内容と整合的です(これは、横のズレ方のチェックに対応しています)。
これらのことから、1, 5, 6 はすべて正しいことがわかります。
ここから先は補足ですが、これらの式が同じ内容であることは次のようにして確認できます。加法定理より、1 は、
\begin{eqnarray}
& &
2\sin\left(2x-\dfrac{\pi}{2}\right) \\[5pt]
&=&
2\left(\sin2x\cos\dfrac{\pi}{2}-\cos2x\sin\dfrac{\pi}{2}\right) \\[5pt]
&=&
-2\cos2x \\[5pt]
\end{eqnarray}となり、5 は
\begin{eqnarray}
2\cos2\left(x-\dfrac{\pi}{2}\right)
&=&
2\cos\left(2x-\pi\right) \\[5pt]
&=&
-2\cos2x \\[5pt]
\end{eqnarray}となり、6 は
\begin{eqnarray}
2\cos2\left(x+\dfrac{\pi}{2}\right)
&=&
2\cos\left(2x+\pi\right) \\[5pt]
&=&
-2\cos2x \\[5pt]
\end{eqnarray}となります。すべて $y=-2\cos 2x$ であり、このグラフが与えられたグラフと同じものになります。
解答
サ:156