共通テスト 数学II・数学B 2017年度プレテスト 第3問 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【選択問題】(第3問~第5問から2問選択)
問題編
問題
次の文章を読んで、下の問いに答えよ。
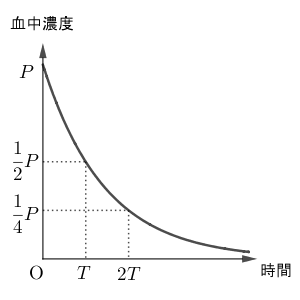
ある薬Dを服用したとき、有効成分の血液中の濃度(血中濃度)は一定の割合で減少し、 $T$ 時間が経過すると $\dfrac{1}{2}$ 倍になる。薬Dを1錠服用すると、服用直後の血中濃度は $P$ だけ増加する。時間 $0$ で血中濃度が $P$ であるとき、血中濃度の変化は次のグラフで表される。適切な効果が得られる血中濃度の最小値を $M$ 、副作用を起こさない血中濃度の最大値を $L$ とする。
薬Dについては、 $M=2$, $L=40$, $P=5$, $T=12$ である。(1) 薬Dについて、12時間ごとに1錠ずつ服用するときの血中濃度の変化は次のグラフのようになる。
$n$ を自然数とする。 $a_n$ は $n$ 回目の服用直後の血中濃度である。 $a_1$ は $P$ と一致すると考えてよい。第 $(n+1)$ 回目の服用直前には、血中濃度は第 $n$ 回目の服用直後から時間の経過に応じて減少しており、薬を服用した直後に血中濃度が $P$ だけ上昇する。この血中濃度が $a_{n+1}$ である。
$P=5$, $T=12$ であるから、数列 $\{a_n\}$ の初項と漸化式は
\begin{eqnarray} & & a_1=\myBox{ア}, \\[5pt] & & a_{n+1}=\dfrac{\myBox{イ} }{\myBox{ウ} }a_n +\myBox{エ}\quad (n=1,2,3,\cdots) \end{eqnarray}となる。数列 $\{a_n\}$ の一般項を求めてみよう。
【考え方1】
数列 $\{a_n-d\}$ が等比数列となるような定数 $d$ を求める。 $d=\myBox{オカ}$ に対して、数列 $\{a_n-d\}$ が公比 $\dfrac{\myBox{キ} }{\myBox{ク} }$ の等比数列になることを用いる。
【考え方2】
階差数列をとって考える。数列 $\{a_{n+1}-a_n\}$ が公比 $\dfrac{\myBox{ケ} }{\myBox{コ} }$ の等比数列になることを用いる。
いずれの考え方を用いても、一般項を求めることができ、\[ a_n=\myBox{サシ} -\myBox{ス} \left( \dfrac{\myBox{セ} }{\myBox{ソ} } \right)^{n-1} \ (n=1,2,3,\cdots) \]である。
(2) 薬Dについては、 $M=2$, $L=40$ である。薬Dを12時間ごとに1錠ずつ服用する場合、 $n$ 回目の服用直前の血中濃度が $a_n-P$ であることに注意して、正しいものを、次の 0 ~ 5 のうちから二つ選べ。 $\myBox{タ}$
0: 4回目の服用までは血中濃度が $L$ を超えないが、5回目の服用直後に血中濃度が $L$ を超える。
1: 5回目の服用までは血中濃度が $L$ を超えないが、服用し続けるといつか必ず $L$ を超える。
2: どれだけ継続して服用しても血中濃度が $L$ を超えることはない。
3: 1回目の服用直後に血中濃度が $P$ に達して以降、血中濃度が $M$ を下回ることはないので、1回目の服用以降は適切な効果が持続する。
4: 2回目までは服用直前に血中濃度が $M$ 未満になるが、2回目の服用以降は、血中濃度が $M$ を下回ることはないので、適切な効果が持続する。
5: 5回目までは服用直前に血中濃度が $M$ 未満になるが、5回目の服用以降は、血中濃度が $M$ を下回ることはないので、適切な効果が持続する。
(3) (1)と同じ服用量で、服用間隔の条件のみを24時間に変えた場合の血中濃度を調べよう。薬Dを24時間ごとに1錠ずつ服用するときの、 $n$ 回目の服用直後の血中濃度を $b_n$ とする。 $n$ 回目の服用直前の血中濃度は $b_n-P$ である。最初の服用から $24n$ 時間経過後の服用直前の血中濃度である $a_{2n+1}-P$ と $b_{n+1}-P$ を比較する。 $b_{n+1}-P$ と $a_{2n+1}-P$ の比を求めると、\[ \dfrac{b_{n+1}-P}{a_{2n+1}-P}=\dfrac{\myBox{チ} }{\myBox{ツ} } \]となる。
(4) 薬Dを24時間ごとに $k$ 錠ずつ服用する場合には、最初の服用直後の血中濃度は $kP$ となる。服用量を変化させても $T$ の値は変わらないものとする。
薬Dを12時間ごとに1錠ずつ服用した場合と24時間ごとに $k$ 錠ずつ服用した場合の血中濃度を比較すると、最初の服用から $24n$ 時間経過後の各服用直前の血中濃度が等しくなるのは、 $k=\myBox{テ}$ のときである。したがって、24時間ごとに $k$ 錠ずつ服用する場合の各服用直前の血中濃度を、12時間ごとに1錠ずつ服用する場合の血中濃度以上とするためには $k\geqq \mybox{テ}$ でなくてはならない。
また、24時間ごとの服用量を $\mybox{テ}$ 錠にするとき、正しいものを、次の 0 ~ 3 のうちから一つ選べ。 $\myBox{ト}$
0: 1回目の服用以降、服用直後の血中濃度が常に $L$ を超える。
1: 4回目の服用直後までの血中濃度は $L$ 未満だが、5回目以降は服用直後の血中濃度が常に $L$ を超える。
2: 9回目の服用直後までの血中濃度は $L$ 未満だが、10回目以降は服用直後の血中濃度が常に $L$ を超える。
3: どれだけ継続して服用しても血中濃度が $L$ を超えることはない。
考え方
見た目は生物ですが、よく見ると数列の問題です。問題文を読みこむのに時間はかかりますが、センター試験よりは計算量はだいぶ少ないです。
(1)は、漸化式を作って一般項を求めるという、よくある流れです。(2)は、(1)で求めた漸化式から考えます。
(3)は、この比が何を表しているのかわかりづらいですが、数列 $\{b_n\}$ の一般項を求めて計算します。
(4)は、(3)を使う方法もありますが、それに気づかなくても解くことはできます。
この問題を解けば、毎日朝と夜に1錠ずつ飲む薬を、毎朝まとめて2錠ずつ飲んだ場合に同じ効果が得られるのかどうか、理解できるでしょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
次の文章を読んで、下の問いに答えよ。
ある薬Dを服用したとき、有効成分の血液中の濃度(血中濃度)は一定の割合で減少し、 $T$ 時間が経過すると $\dfrac{1}{2}$ 倍になる。薬Dを1錠服用すると、服用直後の血中濃度は $P$ だけ増加する。時間 $0$ で血中濃度が $P$ であるとき、血中濃度の変化は次のグラフで表される。適切な効果が得られる血中濃度の最小値を $M$ 、副作用を起こさない血中濃度の最大値を $L$ とする。

薬Dについては、 $M=2$, $L=40$, $P=5$, $T=12$ である。(1) 薬Dについて、12時間ごとに1錠ずつ服用するときの血中濃度の変化は次のグラフのようになる。
$n$ を自然数とする。 $a_n$ は $n$ 回目の服用直後の血中濃度である。 $a_1$ は $P$ と一致すると考えてよい。第 $(n+1)$ 回目の服用直前には、血中濃度は第 $n$ 回目の服用直後から時間の経過に応じて減少しており、薬を服用した直後に血中濃度が $P$ だけ上昇する。この血中濃度が $a_{n+1}$ である。
$P=5$, $T=12$ であるから、数列 $\{a_n\}$ の初項と漸化式は
\begin{eqnarray} & & a_1=\myBox{ア}, \\[5pt] & & a_{n+1}=\dfrac{\myBox{イ} }{\myBox{ウ} }a_n +\myBox{エ}\quad (n=1,2,3,\cdots) \end{eqnarray}となる。
解説
まず、 $a_1$ は1回目の服用直後の血中濃度で、 $P$ と等しい、と問題文にも書いてあるので、 $a_1=5$ です。
$T=12$ なので、12時間後に血中濃度は $\dfrac{1}{2}$ 倍になっています。 $n$ 回目の服用直後の血中濃度は $a_n$ なので、この12時間後にあたる $(n+1)$ 回目の服用直前の血中濃度は $\dfrac{1}{2}a_n$ となっています。このタイミングで1錠服用するので、服用直後は $\dfrac{1}{2}a_n+5$ となります。これが $a_{n+1}$ となるので、\[ a_{n+1}=\dfrac{1}{2}a_n+5 \]となります。
解答
ア:5
イウエ:125
解答編 つづき
問題
数列 $\{a_n\}$ の一般項を求めてみよう。
【考え方1】
数列 $\{a_n-d\}$ が等比数列となるような定数 $d$ を求める。 $d=\myBox{オカ}$ に対して、数列 $\{a_n-d\}$ が公比 $\dfrac{\myBox{キ} }{\myBox{ク} }$ の等比数列になることを用いる。
【考え方2】
階差数列をとって考える。数列 $\{a_{n+1}-a_n\}$ が公比 $\dfrac{\myBox{ケ} }{\myBox{コ} }$ の等比数列になることを用いる。
解説
数列 $\{a_n-d\}$ が等比数列になるとすると、公比を $r$ として\[ a_{n+1}-d=r(a_n-d) \]が成り立ちます。漸化式から\[ \dfrac{1}{2}a_n+5-d=r(a_n-d) \]が成り立ちます。漸化式から $a_n$ は常に正であることがわかるので、 $r=\dfrac{1}{2}$ でないといけません。これを代入すると
\begin{eqnarray}
\dfrac{1}{2}a_n+5-d &=& \dfrac{1}{2}(a_n-d) \\[5pt]
5-d &=& -\dfrac{1}{2}d \\[5pt]
d &=& 10 \\[5pt]
\end{eqnarray}となります。 $r=\dfrac{1}{2}$, $d=10$ とすると、数列 $\{a_n-10\}$ は公比が $\dfrac{1}{2}$ の等比数列となることがわかります。
次に、階差数列を使う方法を考えます。
\begin{eqnarray}
& &
a_{n+2}-a_{n+1} \\[5pt]
&=&
\left(\dfrac{1}{2}a_{n+1}+5\right)-\left(\dfrac{1}{2}a_{n}+5\right) \\[5pt]
&=&
\dfrac{1}{2}\left(a_{n+1}-a_n\right) \\[5pt]
\end{eqnarray}なので、数列 $\{a_{n+1}-a_n\}$ は公比が $\dfrac{1}{2}$ の等比数列になります。
解答
オカ:10
キク:12
ケコ:12
解答編 つづき
問題
いずれの考え方を用いても、一般項を求めることができ、\[ a_n=\myBox{サシ} -\myBox{ス} \left( \dfrac{\myBox{セ} }{\myBox{ソ} } \right)^{n-1} \ (n=1,2,3,\cdots) \]である。
解説
先ほどの考え方1を使うと、数列 $\{a_n-10\}$ は初項が $a_1-10=-5$ で、公比が $\dfrac{1}{2}$ の等比数列なので
\begin{eqnarray}
a_n-10
&=&
-5\left(\dfrac{1}{2}\right)^{n-1}
\end{eqnarray}となるので、一般項は\[ a_n=10-5\left(\dfrac{1}{2}\right)^{n-1} \]と求められます。
解答
サシスセソ:10512
解答編 つづき
問題
(2) 薬Dについては、 $M=2$, $L=40$ である。薬Dを12時間ごとに1錠ずつ服用する場合、 $n$ 回目の服用直前の血中濃度が $a_n-P$ であることに注意して、正しいものを、次の 0 ~ 5 のうちから二つ選べ。 $\myBox{タ}$
0: 4回目の服用までは血中濃度が $L$ を超えないが、5回目の服用直後に血中濃度が $L$ を超える。
1: 5回目の服用までは血中濃度が $L$ を超えないが、服用し続けるといつか必ず $L$ を超える。
2: どれだけ継続して服用しても血中濃度が $L$ を超えることはない。
3: 1回目の服用直後に血中濃度が $P$ に達して以降、血中濃度が $M$ を下回ることはないので、1回目の服用以降は適切な効果が持続する。
4: 2回目までは服用直前に血中濃度が $M$ 未満になるが、2回目の服用以降は、血中濃度が $M$ を下回ることはないので、適切な効果が持続する。
5: 5回目までは服用直前に血中濃度が $M$ 未満になるが、5回目の服用以降は、血中濃度が $M$ を下回ることはないので、適切な効果が持続する。
解説
$n$ 回目の服用直後の血中濃度が $a_n=10-5\left(\dfrac{1}{2}\right)^{n-1}$ となることを利用して考えていきます。
選択肢 0, 1, 2 は、 $a_n$ が $L=40$ を超えるか超えないかについての選択肢です。 $a_n$ の式を見ると、 $10$ から正の値を引くので、 $40$ を超えることはありません。なので、 2 が正しいことがわかります。
選択肢 3, 4, 5 は、 $a_n$ が $M=2$ を下回るかどうかについての選択肢です。時間がたつにつれて血中濃度は下がっていくので、これらの選択肢を考えるには、服用直前、つまり $a_n-5$ がどうなるかを見ていかなくてはいけません。
$\left(\dfrac{1}{2}\right)^{n-1}$ は正の値で、 $n$ が大きくなるほど小さくなっていきます。なので、 $a_n-5=5-5\left(\dfrac{1}{2}\right)^{n-1}$ の値は、 $n$ が大きくなるほど大きくなります。 $a_1=5$ で 12時間後の服用直前は $\dfrac{5}{2}$ となり、その後、各12時間ごとの服用直前の血中濃度は $5$ へと近づいていくことから、 $M=2$ を下回ることはありません。なので、選択肢 3 が正しいことがわかります。
解答
タ:2, 3
解答編 つづき
問題
(3) (1)と同じ服用量で、服用間隔の条件のみを24時間に変えた場合の血中濃度を調べよう。薬Dを24時間ごとに1錠ずつ服用するときの、 $n$ 回目の服用直後の血中濃度を $b_n$ とする。 $n$ 回目の服用直前の血中濃度は $b_n-P$ である。最初の服用から $24n$ 時間経過後の服用直前の血中濃度である $a_{2n+1}-P$ と $b_{n+1}-P$ を比較する。 $b_{n+1}-P$ と $a_{2n+1}-P$ の比を求めると、\[ \dfrac{b_{n+1}-P}{a_{2n+1}-P}=\dfrac{\myBox{チ} }{\myBox{ツ} } \]となる。
解説
$n$ 回目の服用直後の血中濃度は $b_n$ であり、 $(n+1)$ 回目の服用はこの24時間後なので、服用直前の血中濃度は $\dfrac{1}{4}b_n$ となっています。服用により、血中濃度は $P=5$ だけ上がるので、\[ b_{n+1}=\dfrac{1}{4}b_n+5 \]が成り立ちます。
(1)の考え方1と同じようにして、数列 $\{b_n\}$ の一般項を求めます。\[ \alpha=\dfrac{1}{4}\alpha+5 \]とおくと、 $\alpha=\dfrac{20}{3}$ なので、数列 $\left\{b_n-\dfrac{20}{3}\right\}$ は、初項が $5-\dfrac{20}{3}=-\dfrac{5}{3}$ で公比が $\dfrac{1}{4}$ の等比数列となるので、\[ b_n=\dfrac{20}{3}-\dfrac{5}{3}\cdot\dfrac{1}{4^{n-1} } \]となります。
また、
\begin{eqnarray}
& &
a_{2n+1} \\[5pt]
&=&
10-5\left(\dfrac{1}{2}\right)^{2n+1-1} \\[5pt]
&=&
10-5\cdot \dfrac{1}{4^n} \\[5pt]
\end{eqnarray}なので、
\begin{eqnarray}
& &
\dfrac{b_{n+1}-P}{a_{2n+1}-P} \\[5pt]
&=&
\dfrac{\dfrac{20}{3}-\dfrac{5}{3}\cdot\dfrac{1}{4^n}-5}{10-5\cdot \dfrac{1}{4^n}-5} \\[5pt]
&=&
\dfrac{\dfrac{5}{3}-\dfrac{5}{3}\cdot\dfrac{1}{4^n} }{5-5\cdot \dfrac{1}{4^n} } \\[5pt]
&=&
\dfrac{\dfrac{5}{3}\left(1-\dfrac{1}{4^n}\right)}{5\left(1- \dfrac{1}{4^n}\right)} \\[5pt]
&=&
\dfrac{1}{3}
\end{eqnarray}となります。
解答
チツ:13
解答編 つづき
問題
(4) 薬Dを24時間ごとに $k$ 錠ずつ服用する場合には、最初の服用直後の血中濃度は $kP$ となる。服用量を変化させても $T$ の値は変わらないものとする。
薬Dを12時間ごとに1錠ずつ服用した場合と24時間ごとに $k$ 錠ずつ服用した場合の血中濃度を比較すると、最初の服用から $24n$ 時間経過後の各服用直前の血中濃度が等しくなるのは、 $k=\myBox{テ}$ のときである。したがって、24時間ごとに $k$ 錠ずつ服用する場合の各服用直前の血中濃度を、12時間ごとに1錠ずつ服用する場合の血中濃度以上とするためには $k\geqq \mybox{テ}$ でなくてはならない。
また、24時間ごとの服用量を $\mybox{テ}$ 錠にするとき、正しいものを、次の 0 ~ 3 のうちから一つ選べ。 $\myBox{ト}$
0: 1回目の服用以降、服用直後の血中濃度が常に $L$ を超える。
1: 4回目の服用直後までの血中濃度は $L$ 未満だが、5回目以降は服用直後の血中濃度が常に $L$ を超える。
2: 9回目の服用直後までの血中濃度は $L$ 未満だが、10回目以降は服用直後の血中濃度が常に $L$ を超える。
3: どれだけ継続して服用しても血中濃度が $L$ を超えることはない。
解説
(3)を使う方法もありますが、まずはそのまま考えます。
12時間ごとに1錠ずつ服用する場合、1回目の服用直後で血中濃度は $5$ となり、2回目の服用直後で $5\cdot\dfrac{1}{2}+5=\dfrac{15}{2}$ となり、3回目の服用直前では $\dfrac{15}{4}$ となります。
一方、24時間ごとに $k$ 錠ずつ服用する場合、1回目の服用直後で $5k$ となり、2回目(24時間後)の服用直前では $\dfrac{5k}{4}$ となります。
この2つが同じであるとすると、 $\dfrac{15}{4}=\dfrac{5k}{4}$ なので $k=3$ とわかります。
問題を解く上では必要ないですが、他のタイミングでも血中濃度が等しくなることを確認しておきましょう。
$24n$ 時間経過後の服用直前の血中濃度が $x$ であるとします。
12時間ごとに1錠ずつ服用する場合、 $24n$ 時間経過後の服用直後は $x+5$, $(24n+12)$ 時間経過後の服用直後は $\dfrac{x+5}{2}+5=\dfrac{x+15}{2}$ なので、 $24(n+1)$ 時間経過後の服用直前は $\dfrac{x+15}{4}$ となります。
一方、24時間ごとに3錠ずつ服用する場合、 $24n$ 時間の服用直後は $x+5\cdot3=x+15$ なので、 $24(n+1)$ 時間の服用直前は $\dfrac{x+15}{4}$ となり、確かに、 $24n$ 時間経過後の各服用直前の血中濃度が等しくなることがわかります。
このようにして求める方法もありますが、(3)を使う方法もあります。
24時間ごとに1錠ずつ服用する場合、 $24n$ 時間経過後の服用直後の血中濃度は $b_n$ で表されます。薬の量を $k$ 倍すれば、血中濃度も $k$ 倍されるので、 $k$ 錠ずつ服用する場合は $kb_n$ となります。なので、 $24n$ 時間経過後の服用直前の血中濃度は $k(b_{n+1}-P)$ となります。これが $a_{2n+1}-P$ と等しくなるのは $\dfrac{k(b_{n+1}-P)}{a_{2n+1}-P}=\dfrac{k}{3}$ が $1$ になるとき、つまり、 $k=3$ のときだとわかります。
後半部分を考えます。12時間ごとに1錠ずつ服用する場合と、24時間ごとに3錠ずつ服用する場合で、 $24n$ 時間経過後の服用直前の血中濃度が等しくなることから、 $24$ 時間ごとの服用直前の血中濃度は、 $a_3-5$, $a_5-5$, $a_7-5$, … となります。(1)で求めた通り、\[ a_n=10-5\left(\dfrac{1}{2}\right)^{n-1} \]なので、 $24$ 時間ごとの服用直前の血中濃度は、$5$ を超えることはありません。そのため、3錠を服用した直後の血中濃度は $5+5\cdot 3=20$ を超えることはありません。血中濃度が高くなるのは服用直後であり、服用直後で $20$ を超えないのだから、 $L=40$ を超えることはありません。なので、選択肢 3 が正しいです。
ちなみに、この(4)から何がわかるでしょうか。例えば、「この薬Dを朝と夜に1錠ずつ飲んでください」と言われたとします。そして、ついつい夜に飲むのを忘れてしまったとします。このときに「毎朝、まとめて1日分飲めばいいや」と思っても、2錠ずつ飲んだだけでは本来よりも血中濃度が下がってしまうことがわかります。このケースでは、たまたま $M=2$ を下回ることはないので薬の効果はありますが。
また、漸化式を見ると、 $a_n$ はどんどん $10$ に近づいていきますが、 $3b_n$ はどんどん $20$ に近づいていきます。このケースでは、たまたま $L=40$ を超えることはないので問題ないですが、一度にまとめて飲む行為は、副作用を起こす可能性が高まることがわかります。薬の飲み方には気を付けないといけません。
解答
テ:3
ト:3