センター試験数学II・数学B 2018年度追試第1問 [1] 解説

🕒 2018/07/17 🔄 2023/05/01

【必答問題】

問題編

問題

　座標平面上に点$\mathrm{ A }(1,0)$, $\mathrm{ P }(\cos 2\theta,\sin 2\theta)$, $\mathrm{ Q }(2\cos 3\theta, 2\sin 3\theta)$ をとる。 $\theta$ が $\dfrac{\pi}{3}\leqq \theta\lt \pi$ の範囲を動くとき、 $\mathrm{ AP }^2+\mathrm{ PQ }^2$ の最大値と最小値を求めよう。

　$\mathrm{ AP }^2$ は
\begin{eqnarray} \mathrm{ AP }^2 &=& \myBox{ア}-\myBox{イ} \cos 2\theta \\[5pt] &=& \myBox{ウ}-\myBox{エ} \cos^2 \theta \\[5pt] \end{eqnarray}である。また、 $\mathrm{ PQ }^2$ は\[ \mathrm{ PQ }^2=\myBox{オ}-\myBox{カ} \cos \theta \]である。
　$\dfrac{\pi}{3}\leqq \theta\lt \pi$ であるから、 $\myBox{キク}\lt \cos\theta\leqq \dfrac{\myBox{ケ} }{\myBox{コ} }$ である。したがって、 $\mathrm{ AP }^2+\mathrm{ PQ }^2$ は、 $\theta=\dfrac{\myBox{サ} }{\myBox{シ} }\pi$ のとき最大値 $\myBox{スセ}$ をとり、 $\theta=\dfrac{\pi}{\myBox{ソ} }$ のとき最小値 $\myBox{タ}$ をとる。

考え方

PQ の式変形が少し難しいかもしれません。3倍角があるからといって、3倍角の公式をいきなり使ってしまうと計算が大変になってしまいます。ここでの計算結果は後に響いてくるので、計算結果が間違っていないかどうか、 $\theta=0$ などとして、チェックすると安全です。

これを乗り越えるとかなり優しくなります。後半は、ほとんど二次関数の問題です。ソのところは、本来はサシのような式でもいいはずです。こうしたところにも優しさが見えます。

【必答問題】

解答編

問題

　座標平面上に点$\mathrm{ A }(1,0)$, $\mathrm{ P }(\cos 2\theta,\sin 2\theta)$, $\mathrm{ Q }(2\cos 3\theta, 2\sin 3\theta)$ をとる。 $\theta$ が $\dfrac{\pi}{3}\leqq \theta\lt \pi$ の範囲を動くとき、 $\mathrm{ AP }^2+\mathrm{ PQ }^2$ の最大値と最小値を求めよう。

　$\mathrm{ AP }^2$ は
\begin{eqnarray} \mathrm{ AP }^2 &=& \myBox{ア}-\myBox{イ} \cos 2\theta \\[5pt] &=& \myBox{ウ}-\myBox{エ} \cos^2 \theta \\[5pt] \end{eqnarray}である。

解説

点$\mathrm{ A }(1,0)$, $\mathrm{ P }(\cos 2\theta,\sin 2\theta)$ なので、
\begin{eqnarray} \mathrm{ AP }^2 &=& (\cos 2\theta-1)^2+(\sin2\theta-0)^2 \\[5pt] &=& \cos^2 2\theta-2\cos 2\theta+1+\sin^2 2\theta \\[5pt] &=& 2-2\cos 2\theta \\[5pt] \end{eqnarray}となります。また、倍角の公式から \begin{eqnarray} \mathrm{ AP }^2 &=& 2-2\cos 2\theta \\[5pt] &=& 2-2(2\cos^2\theta-1) \\[5pt] &=& 4-4\cos^2\theta \\[5pt] \end{eqnarray}となります。

解答

アイ：22
ウエ：44

参考

解答編つづき

問題

また、 $\mathrm{ PQ }^2$ は\[ \mathrm{ PQ }^2=\myBox{オ}-\myBox{カ} \cos \theta \]である。

解説

点$\mathrm{ P }(\cos 2\theta,\sin 2\theta)$, $\mathrm{ Q }(2\cos 3\theta, 2\sin 3\theta)$ なので、
\begin{eqnarray} \mathrm{ PQ }^2 &=& (2\cos 3\theta-\cos 2\theta)^2+(2\sin 3\theta-\sin 2\theta)^2 \\[5pt] &=& 4\cos^2 3\theta-4\cos 3\theta\cos 2\theta+\cos^2 2\theta \\ & & +4\sin^2 3\theta-4\sin 3\theta\sin 2\theta+\sin^2 2\theta \\[5pt] &=& 4-4(\cos 3\theta\cos 2\theta+\sin 3\theta\sin 2\theta)+1 \\[5pt] \end{eqnarray}となります。最後の式のカッコ内は、三角関数の積を和に変換する公式を2回使ってもいいですが、そもそも、 $\cos\theta$ の加法定理そのままの形をしています。カッコ内は、 $\cos(3\theta-2\theta)$ と変形できますね。よって、 \begin{eqnarray} \mathrm{ PQ }^2 &=& 4-4(\cos 3\theta\cos 2\theta+\sin 3\theta\sin 2\theta)+1 \\[5pt] &=& 5-4\cos (3\theta-2\theta) \\[5pt] &=& 5-4\cos \theta \\[5pt] \end{eqnarray}となります。

解答

オカ：54

参考

【基本】正弦・余弦の加法定理の使い方

解答編つづき

問題

　$\dfrac{\pi}{3}\leqq \theta\lt \pi$ であるから、 $\myBox{キク}\lt \cos\theta\leqq \dfrac{\myBox{ケ} }{\myBox{コ} }$ である。したがって、 $\mathrm{ AP }^2+\mathrm{ PQ }^2$ は、 $\theta=\dfrac{\myBox{サ} }{\myBox{シ} }\pi$ のとき最大値 $\myBox{スセ}$ をとり、 $\theta=\dfrac{\pi}{\myBox{ソ} }$ のとき最小値 $\myBox{タ}$ をとる。

解説

ここまでくれば、後は数学Iの範囲の内容ですね。

$\dfrac{\pi}{3}\leqq \theta\lt \pi$ のとき、 $\cos\theta$ のとる値は、\[ -1\lt \cos\theta \leqq \frac{1}{2} \]となります。この範囲で、 $\mathrm{ AP }^2+\mathrm{ PQ }^2$ の最大・最小を求めましょう。
\begin{eqnarray} & & \mathrm{ AP }^2+\mathrm{ PQ }^2 \\ &=& (4-4\cos^2\theta)+(5-4\cos\theta) \\ &=& -4\cos^2\theta -4\cos\theta +9 \\ \end{eqnarray}となります。 $x=\cos\theta$ とおき、 $-1\lt x \leqq \dfrac{1}{2}$ の範囲で、 $y=-4x^2-4x+9$ の最大・最小を考えてみましょう。 \begin{eqnarray} y &=& -4x^2-4x+9 \\[5pt] &=& -4\left(x+\dfrac{1}{2}\right)^2+10 \\[5pt] \end{eqnarray}となるので、グラフは以下のようになります。

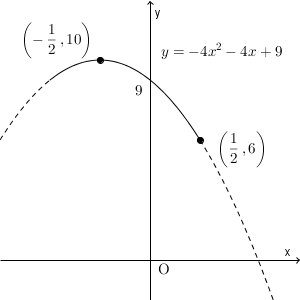
よって、最大となるのは、 $x=-\dfrac{1}{2}$ のとき、つまり、 $\theta=\dfrac{2}{3}\pi$ のときで、そのときの値は $10$ です。最小値は、 $x=\dfrac{1}{2}$ のとき、つまり、 $\theta=\dfrac{\pi}{3}$ のときで、そのときの値は $6$ となることがわかります。