センター試験 数学II・数学B 2006年度 第2問 解説
問題編
【問題】
aを正の実数として、$C_1,C_2$をそれぞれ次の2次関数のグラフとする。
\begin{eqnarray} & & C_1: y=x^2 \\ & & C_2: y=x^2 -4ax+4a(a+1) \end{eqnarray}また、$C_1$と$C_2$の両方に接する直線をlとする。(1) 点$(t,t^2)$における$C_1$の接線の方程式は\[ y=[ア]tx-t^{[イ]} \]であり、この直線が$C_2$に接するのは$t=[ウ]$のときである。
したがって、直線lの方程式は\[ y=[エ]x-[オ] \]であり、lと$C_2$の接点の座標は\[ ([カキ]+[ク],[ケコ]+[サ]) \]である。
(2) $C_1$と$C_2$の交点をPとすると、Pの座標は\[ (a+[シ],(a+[シ])^2) \]である。点Pを通って直線lに平行な直線をmとする。直線mの方程式は\[ y=[ス]x+a^{[セ]}-[ソ] \]である。直線mとy軸との交点のy座標が正となるようなaの値の範囲は$a\gt [タ]$である。
$a\gt [タ]$のとき、$C_1$の$x\geqq 0$の部分と直線mおよびy軸で囲まれた図形の面積Sはaを用いて\[ S = \frac{[チ]}{[ツ]} ([テ]+1)^{[ト]}([ナニ]-1) \]と表される。
【考え方】
(1)は、$C_1$の接線が$C_2$にも接する、と考えて解いていきます。
(2)の最後は、積分区間を求めて積分をします。$a$が入っていて計算しにくいですが、共通項でくくりながら計算すると、少しだけ計算量がへります。
解答編
【問題】
aを正の実数として、$C_1,C_2$をそれぞれ次の2次関数のグラフとする。
\begin{eqnarray} & & C_1: y=x^2 \\ & & C_2: y=x^2 -4ax+4a(a+1) \end{eqnarray}また、$C_1$と$C_2$の両方に接する直線をlとする。(1) 点$(t,t^2)$における$C_1$の接線の方程式は\[ y=[ア]tx-t^{[イ]} \]であり、この直線が$C_2$に接するのは$t=[ウ]$のときである。
【解説】
$y=x^2$を微分すると$y'=2x$なので、点$(t,t^2)$における$C_1$の接線の方程式は
\begin{eqnarray}
y
&=&
2t(x-t)+t^2 \\
&=&
2tx-t^2 \\
\end{eqnarray}となります。この直線lと$C_2$との交点のx座標は
\begin{eqnarray}
x^2 -4ax +4a(a+1) &=& 2tx-t^2 \\
x^2 -(4a+2t)x +4a(a+1)+t^2 &=& 0 \\
\end{eqnarray}を満たします。直線lが$C_2$が接するには、この方程式が重解を持てばいいので、
\begin{eqnarray}
(4a+2t)^2 - 4\left\{ 4a(a+1)+t^2 \right\} &=& 0\\
(2a+t)^2 - 4a^2 -4a -t^2 &=& 0\\
4at -4a &=& 0\\
a(t -1) &=& 0\\
\end{eqnarray}となります。$a\gt 0$なので、これより$t=1$がわかります。
【解答】
アイ:22
ウ:1
【問題】
したがって、直線lの方程式は\[ y=[エ]x-[オ] \]であり、lと$C_2$の接点の座標は\[ ([カキ]+[ク],[ケコ]+[サ]) \]である。
【解説】
先ほど求めた通り、$C_1$の接線の方程式は、$y=2tx-t^2$であり、直線lの式は$t=1$としたものなので、$y=2x-1$となります。
また、これも先ほど求めた通り、直線lと$C_2$との交点のx座標は
\begin{eqnarray}
x^2 -(4a+2t)x +4a(a+1)+t^2 &=& 0
\end{eqnarray}を満たします。これに$t=1$を代入すると
\begin{eqnarray}
x^2 -(4a+2)x +4a^2+4a+1 &=& 0 \\
x^2 -2(2a+1)x +(2a+1)^2 &=& 0 \\
\{ x -(2a+1) \}^2 &=& 0
\end{eqnarray}より、$x=2a+1$がわかります。y座標は、直線lの方程式に代入して
\begin{eqnarray}
y
&=&
2(2a+1)-1 \\
&=&
4a+1
\end{eqnarray}と求められます。
【解答】
エオ:21
カキク:2a1
ケコサ:4a1
【問題】
(2) $C_1$と$C_2$の交点をPとすると、Pの座標は\[ (a+[シ],(a+[シ])^2) \]である。
【解説】
交点のx座標は、
\begin{eqnarray}
x^2 &=& x^2 -4ax+4a(a+1) \\
4ax &=& 4a(a+1) \\
x &=& a+1
\end{eqnarray}となります。
【解答】
シ:1
【問題】
点Pを通って直線lに平行な直線をmとする。直線mの方程式は\[ y=[ス]x+a^{[セ]}-[ソ] \]である。
【解説】
直線mは直線lと平行なので、傾きは$2$となります。これが点Pを通るので、直線mの方程式は
\begin{eqnarray}
y
&=&
2\{ x -(a+1) \} +(a+1)^2 \\
&=&
2x -2(a+1) +(a^2+2a+1) \\
&=&
2x +a^2-1
\end{eqnarray}となります。
【解答】
スセソ:221
【問題】
直線mとy軸との交点のy座標が正となるようなaの値の範囲は$a\gt [タ]$である。
【解説】
直線mの方程式は$y=2x +a^2-1$なので、この直線とy軸との交点のy座標は、$a^2-1$となります。仮定よりaは正なので、$a^2-1$が正となるのは、$a\gt 1$のときであることがわかります。
【解答】
タ:1
【問題】
$a\gt [タ]$のとき、$C_1$の$x\geqq 0$の部分と直線mおよびy軸で囲まれた図形の面積Sはaを用いて\[ S = \frac{[チ]}{[ツ]} ([テ]+1)^{[ト]}([ナニ]-1) \]と表される。
【解説】
面積を求める部分は、次の図の色のついている部分です。
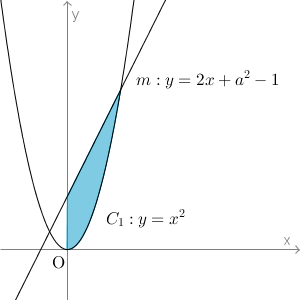
面積を求めるには積分をすればいいのですが、積分区間がわかりません。つまり、面積を求める前に、直線mと$C_1$との交点を求めないといけません。
\begin{eqnarray}
x^2 &=& 2x+a^2-1 \\
x^2 -2x -(a+1)(a-1) &=& 0 \\
\{x-(a+1)\}\{x+(a-1)\} &=& 0 \\
\end{eqnarray}なので、$x=a+1,-a+1$となります。ここで、$a\gt 1$なので、$x\gt 0$となるものは、$x=a+1$だけになります。
よって、面積Sは
\begin{eqnarray}
S
&=&
\int_0^{a+1} (2x+a^2-1 -x^2)dx \\[5pt]
&=&
\left[ x^2+(a^2-1)x -\frac{x^3}{3} \right]_0^{a+1} \\[5pt]
&=&
(a+1)^2+(a^2-1)(a+1) -\frac{(a+1)^3}{3} \\[5pt]
&=&
\frac{3(a+1)^2+3(a-1)(a+1)^2 -(a+1)^3}{3} \\[5pt]
&=&
\frac{(a+1)^2 (3+3a-3 -a-1)}{3} \\[5pt]
&=&
\frac{1}{3} (a+1)^2 (2a-1) \\[5pt]
\end{eqnarray}と求めることができます。
【解答】
チツ:13
テトナニ:a22a





