センター試験 数学II・数学B 2006年度 第1問 [1] 解説
問題編
【問題】
$0^{\circ}\leqq \theta \lt 180^{\circ}$の範囲で関数$f(\theta)=3\cos 2\theta+4\sin\theta$を考える。$\sin\theta = t$とおけば\[ \cos 2\theta = [ア] -[イ]t^{[ウ]} \]であるから、$y=f(\theta)$とおくと\[ y=-[エ]t^{[ウ]} +[オ]t +[カ] \]である。したがって、yの最大値は$\displaystyle \frac{[キク]}{3}$であり、最小値は$[ケ]$である。
また、$\alpha$が$0^{\circ}\lt \alpha \lt 90^{\circ}$を満たす角度で$f(\alpha)=3$のとき\[ \sin( \alpha +30^{\circ}) =\frac{[コ]\sqrt{[サ]}+\sqrt{[シ]} }{[ス]} \]である。
【考え方】
$\cos$や$\sin$を別の文字で置き換えて考えていく、というよくある問題です。ここでは、$\sin$をtで置き換えています。tの範囲に注意して解いていきます。
最後は加法定理を用いたあと、$\sin\alpha$と$\cos\alpha$を求めましょう。
解答編
【問題】
$0^{\circ}\leqq \theta \lt 180^{\circ}$の範囲で関数$f(\theta)=3\cos 2\theta+4\sin\theta$を考える。$\sin\theta = t$とおけば\[ \cos 2\theta = [ア] -[イ]t^{[ウ]} \]であるから、$y=f(\theta)$とおくと\[ y=-[エ]t^{[ウ]} +[オ]t +[カ] \]である。
【解説】
倍角の公式より、$\cos 2\theta=1-2\sin^2\theta$なので、\[ \cos2\theta=1-2t^2 \]となります。
このことから、
\begin{eqnarray}
y
&=&
3\cos 2\theta + 4\sin\theta \\
&=&
3(1-2t^2) + 4t \\
&=&
-6t^2 + 4t +3
\end{eqnarray}となります。
【解答】
アイウ:122
エオカ:643
【問題】
したがって、yの最大値は$\displaystyle \frac{[キク]}{3}$であり、最小値は$[ケ]$である。
【解説】
今、$0^{\circ}\leqq \theta \lt 180^{\circ}$の範囲で考えているので、$t = \sin\theta$の範囲は、$0\leqq t \leqq 1$となります。この範囲で、$y=-6t^2 + 4t +3$の最大値と最小値を考えます。
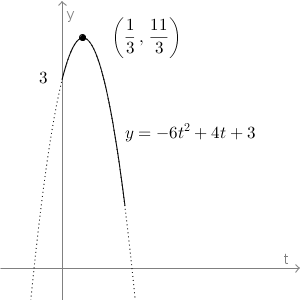
このことから、$t=\frac{1}{3}$のときに、最大値$\frac{11}{3}$をとることがわかります。また、$t=0$のとき$y=3$、$t=1$のとき$y=-6+4+3=1$なので、最小値は$1$となることがわかります。
【解答】
キク:11
ケ:1
【問題】
また、$\alpha$が$0^{\circ}\lt \alpha \lt 90^{\circ}$を満たす角度で$f(\alpha)=3$のとき\[ \sin( \alpha +30^{\circ}) =\frac{[コ]\sqrt{[サ]}+\sqrt{[シ]} }{[ス]} \]である。
【解説】
$\sin( \alpha +30^{\circ})$を直接求めるのは無理なので、加法定理を用いて次のように変形します。
\begin{eqnarray}
\sin( \alpha +30^{\circ})
&=&
\sin\alpha \cos 30^{\circ} + \cos\alpha \sin 30^{\circ} \\[5pt]
&=&
\frac{\sqrt{3}\sin\alpha + \cos\alpha }{2} \quad\cdots (1)
\end{eqnarray}これを求めるには、$\sin\alpha$が分かればいいですね。
先ほどと同じように、$\sin\alpha=s$とおけば、$f(\alpha)=-6s^2+4s+3$なので、$f(\alpha)=3$となるのは、
\begin{eqnarray}
-6s^2+4s+3 &=& 3 \\
s(3s-2) &=& 0 \\
\end{eqnarray}より、$s=0,\frac{2}{3}$のときであることがわかります。$\alpha$は$0^{\circ}\lt \alpha \lt 90^{\circ}$なので、$0\lt s \lt 1$だから、$s=\frac{2}{3}$となります。つまり、$\sin\alpha=\frac{2}{3}$です。
この範囲では、$0 \lt \cos\alpha \lt 1$なので、
\begin{eqnarray}
\cos\alpha
&=&
\sqrt{1-\sin^2\alpha} \\[5pt]
&=&
\sqrt{1-\left(\frac{2}{3}\right)^2} \\[5pt]
&=&
\frac{\sqrt{5} }{3} \\[5pt]
\end{eqnarray}となります。
これらを(1)に代入すれば
\begin{eqnarray}
\sin( \alpha +30^{\circ})
&=&
\frac{\sqrt{3}\sin\alpha + \cos\alpha }{2} \\[5pt]
&=&
\frac{\sqrt{3}\cdot\frac{2}{3} + \frac{\sqrt{5} }{3} }{2} \\[5pt]
&=&
\frac{2\sqrt{3} + \sqrt{5} }{6}
\end{eqnarray}と求めることができます。
【解答】
コサシス:2356





