センター試験 数学II・数学B 2006年度 第1問 [2] 解説
問題編
【問題】
不等式\[ 2\log_3 x -4\log_x 27 \leqq 5 \quad \cdots (*) \]が成り立つようなxの範囲を求めよう。(1) 不等式(*)において、xは対数の底であるから
$x\gt [セ]$ かつ $x\ne [ソ]$
を満たさなければならない。また\[\log_x27=\frac{[タ]}{\log_3 x}\]である。(2) 不等式(*)は
$[セ]\lt x \lt [ソ]$のとき \[ [チ](\log_3 x)^2 -[ツ]\log_3 x -[テト] \geqq 0 \]
$x \gt [ソ]$のとき \[ [チ](\log_3 x)^2 -[ツ]\log_3 x -[テト] \leqq 0 \]
と変形できる。したがって、求めるxの値の範囲は\[ [セ]\lt x \leqq \frac{\sqrt{[ナ]} }{[ニ]}, \quad [ソ]\lt x \leqq[ヌネ] \]である。
【考え方】
$\log$の部分を別の文字で置き換えて考えていく、というよくあるタイプの問題です。不等式なので、$\log$の値が正か負かで場合分けをして考えていく必要があります。
最終的に出てくる式は2次不等式であり、因数分解もできるので難しい式ではありませんが、場合分けが少し面倒です。穴埋めなので不等号の向きを間違っても答えを出すことはできますが、穴埋めでなくても正しく解けるようになっていることが望ましいです。
解答編
【問題】
不等式\[ 2\log_3 x -4\log_x 27 \leqq 5 \quad \cdots (*) \]が成り立つようなxの範囲を求めよう。(1) 不等式(*)において、xは対数の底であるから
$x\gt [セ]$ かつ $x\ne [ソ]$
を満たさなければならない。
【解説】
$\log_x 27=a$とすると、$x^a=27$となります。このような定義ができるのは、xが正のときしかありません。また、xが正でも、1のときはこれを満たすaはありません。よって、$x\gt 0$かつ$x\ne 1$です。
この問題は、対数を扱う「前提」を知っているかを問う問題で、考えて解く問題というよりは知識を問う問題に近いです。
【解答】
セソ:01
【問題】
また\[\log_x27=\frac{[タ]}{\log_3 x}\]である。
【解説】
底の変換公式より
\begin{eqnarray}
\log_x27
&=&
\frac{\log_3 27}{\log_3 x} \\[5pt]
&=&
\frac{3}{\log_3 x}
\end{eqnarray}となります。
【解答】
タ:3
【問題】
(2) 不等式(*)は
$[セ]\lt x \lt [ソ]$のとき \[ [チ](\log_3 x)^2 -[ツ]\log_3 x -[テト] \geqq 0 \]
$x \gt [ソ]$のとき \[ [チ](\log_3 x)^2 -[ツ]\log_3 x -[テト] \leqq 0 \]
と変形できる。
(1)の最後から$\displaystyle \log_x 27=\frac{3}{\log_3 x}$なので、これを(*)に代入すると
\begin{eqnarray}
2\log_3 x -4\log_x 27 & \leqq & 5 \\[5pt]
2\log_3 x -4\cdot \frac{3}{\log_3 x} & \leqq & 5 \\[5pt]
\end{eqnarray}となります。この両辺に$\log_3 x$を掛けたいのですが、これが正か負かで不等号の向きが変わってしまうので、場合分けをします。
$\log_3 x \lt 0$のとき、つまり、$0 \lt x \lt 1$のときは、
\begin{eqnarray}
2(\log_3 x)^2 -12 & \geqq & 5(\log_3 x) \\[5pt]
2(\log_3 x)^2 -5\log_3 x -12 & \geqq & 0
\end{eqnarray}となります。
$\log_3 x \gt 0$のとき、つまり、$x \gt 1$のときは、
\begin{eqnarray}
2(\log_3 x)^2 -12 & \leqq & 5(\log_3 x) \\[5pt]
2(\log_3 x)^2 -5\log_3 x -12 & \leqq & 0
\end{eqnarray}となります。
【解答】
チツテト:2512
【問題】
したがって、求めるxの値の範囲は\[ [セ]\lt x \leqq \frac{\sqrt{[ナ]} }{[ニ]}, \quad [ソ]\lt x \leqq[ヌネ] \]である。
【解説】
$2(\log_3 x)^2 -5\log_3 x -12$について考えます。そのままだと考えづらいので、$t=\log_3 x$と置いてみると、\[
2t^2-5t-12=(2t+3)(t-4)\]と変形できます。よって、$y=2t^2-5t-12$のグラフは次のようになります。
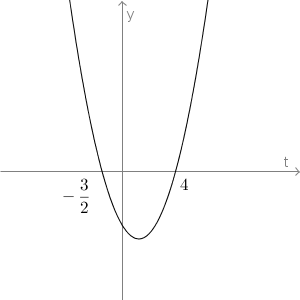
先ほどの場合分けと、このグラフから、不等式を解いていきます。
$\log_3 x \lt 0$のとき、つまり、$t\lt 0$のときは、\[ 2t^2 -5t -12 \geqq 0 \]なので、$\displaystyle t\leqq -\frac{3}{2}$となります。このとき、xは
\begin{eqnarray}
\log_3 x & \leqq & -\frac{3}{2} \\
x & \leqq & 3^{-\frac{3}{2} } \\
x & \leqq & \frac{\sqrt{3} }{9}
\end{eqnarray}となります。もともと$0 \lt x \lt 1$の範囲を考えていたので、\[ 0 \lt x \leqq \frac{\sqrt{3} }{9} \]となります。
一方、$\log_3 x \gt 0$のとき、つまり、$t\gt 0$のときは、\[ 2t^2 -5t -12 \leqq 0 \]なので、$\displaystyle t\leqq 4$となります。このとき、xは
\begin{eqnarray}
\log_3 x & \leqq & 4 \\
x & \leqq & 3^4 \\
x & \leqq & 81
\end{eqnarray}となります。もともと$x \gt 1$の範囲を考えていたので、\[ 1 \lt x \leqq 81 \]となります。
以上から、求める範囲は、\[ 0 \lt x \leqq \frac{\sqrt{3} }{9} , \quad 1 \lt x \leqq 81 \]となります。
【解答】
ナニ:39
ヌネ:81





