センター試験 数学I・数学A 2020年度 第2問 [1] 解説
【必答問題】
問題編
問題
$\triangle \mathrm{ABC}$ において、 $\mathrm{BC}=2\sqrt{2}$ とする。 $\angle \mathrm{ACB}$ の二等分線と辺 $\mathrm{AB}$ の交点を $\mathrm{D}$ とし、 $\mathrm{CD}=\sqrt{2}$, $\cos\angle \mathrm{BCD}=\dfrac{3}{4}$ とする。このとき、 $\mathrm{BD}=\myBox{ア}$ であり\[ \sin\angle \mathrm{ADC}=\dfrac{\sqrt{\myBox{イウ} }}{\myBox{エ} } \]である。 $\dfrac{\mathrm{AC} }{\mathrm{AD} }=\sqrt{\myBox{オ} }$ であるから\[ \mathrm{AD}=\myBox{カ} \]である。また、 $\triangle\mathrm{ABC}$ の外接円の半径は $\dfrac{\myBox{キ}\sqrt{\myBox{ク} }}{\myBox{ケ} }$ である。
考え方
アは三角形 $\mathrm{BCD}$ について考えますが、イウエではいきなり三角形 $\mathrm{ACD}$ の話に飛んでしまいます。しかし、三角形 $\mathrm{BCD}$ の中でいろいろ考えれば、イウエも求められるようになります。少し難しいです。
カはさらに難しく、ほぼノーヒントです。辺の比を利用して、正弦定理や余弦定理から、辺の長さを求める方程式を作りましょう。
最後のキクケは、正弦定理を使う雰囲気がありますが、どの角も正弦の値がわかりません。今までに求めたことを利用して、どれかの角の正弦を求めましょう。
【必答問題】
解答編
問題
$\triangle \mathrm{ABC}$ において、 $\mathrm{BC}=2\sqrt{2}$ とする。 $\angle \mathrm{ACB}$ の二等分線と辺 $\mathrm{AB}$ の交点を $\mathrm{D}$ とし、 $\mathrm{CD}=\sqrt{2}$, $\cos\angle \mathrm{BCD}=\dfrac{3}{4}$ とする。このとき、 $\mathrm{BD}=\myBox{ア}$ であり\[ \sin\angle \mathrm{ADC}=\dfrac{\sqrt{\myBox{イウ} }}{\myBox{エ} } \]である。
解説
図は次のようになっています。
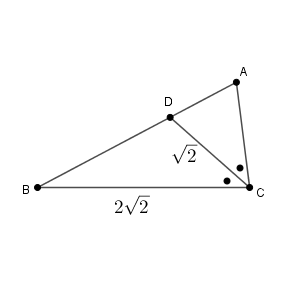
この時点ではまだいろいろな線分の長さや角の大きさがわかっていないので、上と同じ形の図がかけていなくても問題ありません。この時点では、ざっくりとした図をかいておきます。
$\cos\angle \mathrm{BCD}=\dfrac{3}{4}$ と2つの辺の長さがわかっているので、 $\mathrm{BD}$ の長さは、余弦定理を用いて次のようにして求められます。
\begin{eqnarray}
\mathrm{BD}^2
&=&
\mathrm{BC}^2+\mathrm{CD}^2-2\cdot\mathrm{BC}\cdot \mathrm{CD}\cdot \cos\angle \mathrm{BCD} \\[5pt]
&=&
8+2-2\cdot2\sqrt{2}\cdot \sqrt{2}\cdot \dfrac{3}{4} \\[5pt]
&=&
4
\end{eqnarray}これより、 $\mathrm{BD}=2$ となります。
次に、 $\sin\angle \mathrm{ADC}$ を求めます。 $\angle\mathrm{ADC}=180^{\circ}-\angle\mathrm{BDC}$ なので、2つの角の正弦は等しいため、 $\sin\angle\mathrm{BDC}$ を求めます。
相互関係から\[\sin\angle \mathrm{BCD}=\sqrt{1-\left(\dfrac{3}{4}\right)^2}=\dfrac{\sqrt{7} }{4}\]となります。正弦定理より
\begin{eqnarray}
\dfrac{\mathrm{BD} }{\sin\angle\mathrm{BCD} } &=& \dfrac{\mathrm{BC} }{\sin\angle\mathrm{BDC} } \\[5pt]
\dfrac{2}{\dfrac{\sqrt{7} }{4} } &=& \dfrac{2\sqrt{2} }{\sin\angle\mathrm{BDC} } \\[5pt]
\sin\angle\mathrm{BDC} &=& 2\sqrt{2}\cdot \frac{\sqrt{7} }{8} \\[5pt]
&=&
\frac{\sqrt{14} }{4} \\[5pt]
\end{eqnarray}と求められます。
解答
アイウエ:2144
解答編 つづき
問題
$\dfrac{\mathrm{AC} }{\mathrm{AD} }=\sqrt{\myBox{オ} }$ であるから\[ \mathrm{AD}=\myBox{カ} \]である。
解説

辺の比は、次のようにして正弦定理から求めることができます。
\begin{eqnarray}
\dfrac{\mathrm{AC} }{\sin\angle\mathrm{ADC} } &=& \dfrac{\mathrm{AD} }{\sin\angle\mathrm{ACD} } \\[5pt]
\dfrac{\mathrm{AC} }{\mathrm{AD} } &=& \dfrac{\sin\angle\mathrm{ADC} }{\sin\angle\mathrm{ACD} } \\[5pt]
&=&
\dfrac{\dfrac{\sqrt{14} }{4} }{\dfrac{\sqrt{7} }{4} } \\[5pt]
&=&
\sqrt{2}
\end{eqnarray}となります(角の二等分線の性質から、 $\mathrm{AC}:\mathrm{AD}=\mathrm{BC}:\mathrm{BD}$ となることを用いても出せます)。
余弦定理から、
\begin{eqnarray}
\cos\angle \mathrm{ACD}
&=&
\dfrac{\mathrm{CD}^2+\mathrm{AC}^2-\mathrm{AD}^2}{2\cdot \mathrm{CD}\cdot \mathrm{AC} } \\[5pt]
\dfrac{3}{4}
&=&
\dfrac{2+2\mathrm{AD}^2-\mathrm{AD}^2}{2\cdot \sqrt{2}\cdot \sqrt{2}\mathrm{AD} } \\[5pt]
\dfrac{3}{4}
&=&
\dfrac{2+\mathrm{AD}^2}{4\mathrm{AD} } \\[5pt]
2+\mathrm{AD}^2 &=& 3\mathrm{AD} \\[5pt]
\mathrm{AD}^2-3\mathrm{AD}+2 &=& 0 \\[5pt]
(\mathrm{AD}-1)(\mathrm{AD}-2) &=& 0 \\[5pt]
\mathrm{AD} &=& 1,2
\end{eqnarray}となります。ここで、 $\mathrm{AD}=2$ とすると、 $\mathrm{AC}=2\sqrt{2}$ となり、三角形 $\mathrm{ABC}$ は二等辺三角形になってしまいますが、 $\angle \mathrm{ADC}$ が直角でないことから不適であることがわかります。よって、 $\mathrm{AD}=1$ です。
解答
オカ:21
解答編 つづき
問題
また、 $\triangle\mathrm{ABC}$ の外接円の半径は $\dfrac{\myBox{キ}\sqrt{\myBox{ク} }}{\myBox{ケ} }$ である。
解説
$\mathrm{AD}=1$ なので $\mathrm{AC}=\sqrt{2}$ となることから、三角形 $\mathrm{ACD}$ は二等辺三角形となることがわかります。
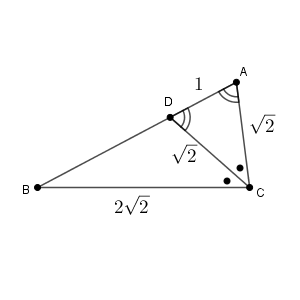
$\angle \mathrm{CAD}=\angle \mathrm{CDA}$ なので、 $\sin\angle\mathrm{CAD}=\sin\angle\mathrm{ADC}=\dfrac{\sqrt{14} }{4}$ です。よって、 三角形 $\mathrm{ABC}$ の外接円の半径 $R$ は、正弦定理から、
\begin{eqnarray}
2R &=& \dfrac{\mathrm{BC} }{\sin\angle\mathrm{BAC} } \\[5pt]
2R &=& \dfrac{2\sqrt{2} }{\dfrac{\sqrt{14} }{4} } \\[5pt]
2R &=& \dfrac{8}{\sqrt{7} } \\[5pt]
R &=& \dfrac{4\sqrt{7} }{7} \\[5pt]
\end{eqnarray}となります。
解答
キクケ:477





