センター試験 数学I・数学A 2019年度 第5問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=4$, $\mathrm{ BC }=7$, $\mathrm{ AC }=5$ とする。このとき、 $\cos \angle \mathrm{ BAC }=-\dfrac{1}{5}$, $\sin\angle \mathrm{ BAC }=\dfrac{2\sqrt{6} }{5}$ である。
$\triangle \mathrm{ ABC }$ の内接円の半径は $\dfrac{\sqrt{\myBox{ア} }}{\myBox{イ} }$ である。
この内接円と辺 AB との接点を D、辺 AC との接点を E とする。
\begin{eqnarray} \mathrm{ AD }&=&\myBox{ウ} \\[5pt] \mathrm{ DE }&=&\dfrac{\myBox{エ}\sqrt{\myBox{オカ} }}{\myBox{キ} } \\[5pt] \end{eqnarray}である。線分 BE と線分 CD の交点を P、直線 AP と辺 BC の交点を Q とする。\[ \frac{\mathrm{ BQ } }{\mathrm{ CQ } }=\frac{\myBox{ク} }{\myBox{ケ} } \]であるから、 $\mathrm{ BQ }=\myBox{コ}$ であり、 $\triangle \mathrm{ ABC }$ の内接円を I とすると\[ \mathrm{ IQ }=\frac{\sqrt{\myBox{サ} }}{\myBox{シ} } \]である。また、直線 CP と $\triangle \mathrm{ ABC }$ の内接円との交点で D とは異なる点を F とすると\[ \cos\angle \mathrm{ DFE }=\dfrac{\myBox{スセ} }{\myBox{ソ} } \]である。
考え方
三角比が何回か登場します。あまりないパターンですが、三角比の内容をガッツリ使うわけではありません。といっても、前半は三角比で解いたほうがわかりやすいかもしれません。図形的に解くには、面積に着目するなどの方法を使いましょう。
後半は、何を使うかは書いていませんが、式の形から何を使うかが予想できるでしょう。最後は、余弦定理などを使うのかな、と思いきや、特に必要ありません。わかりやすい、同じ大きさの角を探しましょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=4$, $\mathrm{ BC }=7$, $\mathrm{ AC }=5$ とする。このとき、 $\cos \angle \mathrm{ BAC }=-\dfrac{1}{5}$, $\sin\angle \mathrm{ BAC }=\dfrac{2\sqrt{6} }{5}$ である。
$\triangle \mathrm{ ABC }$ の内接円の半径は $\dfrac{\sqrt{\myBox{ア} }}{\myBox{イ} }$ である。
解説

C から AB に垂線を下ろして考えると、 $\sin\angle \mathrm{ BAC }=\dfrac{2\sqrt{6} }{5}$ というヒントから、高さが $2\sqrt{6}$ なので、三角形 ABC の面積は
\begin{eqnarray}
\frac{1}{2}\cdot 4 \cdot 2\sqrt{6}
&=&
4\sqrt{6} \\[5pt]
\end{eqnarray}となります。

三角形 ABC の内接円の中心を I とし、上の実線のように三角形を分けてみます。内接円の半径を $r$ とすると
\begin{eqnarray}
\frac{r}{2}(\mathrm{ AB+BC+CA }) &=& 4\sqrt{6} \\[5pt]
r &=& 4\sqrt{6}\cdot\frac{2}{4+7+5} \\[5pt]
&=& \frac{\sqrt{6} }{2} \\[5pt]
\end{eqnarray}となります。
解答
アイ:62
解答編 つづき
問題
この内接円と辺 AB との接点を D、辺 AC との接点を E とする。
\begin{eqnarray} \mathrm{ AD }&=&\myBox{ウ} \\[5pt] \mathrm{ DE }&=&\dfrac{\myBox{エ}\sqrt{\myBox{オカ} }}{\myBox{キ} } \\[5pt] \end{eqnarray}である。
解説

$\mathrm{ AD }=x$ とすると、 $\mathrm{ BD }=4-x$ となります。また、 $\mathrm{ AE }$ も $x$ なので、 $\mathrm{ CE }=5-x$ です。この2つを足すと $\mathrm{ BC }$ になるので、
\begin{eqnarray}
(4-x)+(5-x) &=& 7 \\[5pt]
x &=& 1 \\[5pt]
\end{eqnarray}となります。
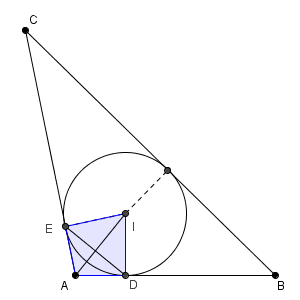
次に、四角形 ADIE の面積を考えてみましょう。
三角形 ADI の2倍、と考えると\[ 2\times \frac{1\cdot \frac{\sqrt{6} }{2} }{2}=\frac{\sqrt{6} }{2} \]となります。また、 AI と DE は垂直に交わるので、次のように面積を出すこともできます。
\begin{eqnarray}
\frac{1}{2}\cdot \mathrm{ AI }\cdot \mathrm{ DE }
&=&
\frac{1}{2}\sqrt{1^2+\left(\frac{\sqrt{6} }{2}\right)^2}\cdot \mathrm{ DE } \\[5pt]
&=&
\frac{\sqrt{10} }{4}\mathrm{ DE }
\end{eqnarray}となります。この2つは同じ面積なので
\begin{eqnarray}
\frac{\sqrt{10} }{4}\mathrm{ DE } &=& \frac{\sqrt{6} }{2} \\[5pt]
\mathrm{ DE } &=& \frac{\sqrt{6}\cdot 4}{2\cdot \sqrt{10} } \\[5pt]
&=& \frac{2\sqrt{15} }{5} \\[5pt]
\end{eqnarray}と求められます。
他の方法として、 DE を余弦定理を用いて求め、それから AD も余弦定理で求める、というやり方もあります。
解答
ウ:1
エオカキ:2155
解答編 つづき
問題
線分 BE と線分 CD の交点を P、直線 AP と辺 BC の交点を Q とする。\[ \frac{\mathrm{ BQ } }{\mathrm{ CQ } }=\frac{\myBox{ク} }{\myBox{ケ} } \]であるから、 $\mathrm{ BQ }=\myBox{コ}$ であり、 $\triangle \mathrm{ ABC }$ の内接円を I とすると\[ \mathrm{ IQ }=\frac{\sqrt{\myBox{サ} }}{\myBox{シ} } \]である。
解説
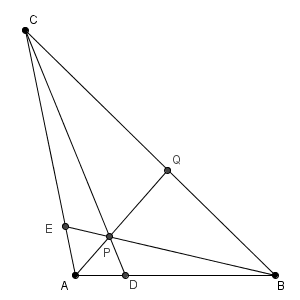
チェバの定理から
\begin{eqnarray}
\frac{\mathrm{ AD } }{\mathrm{ DB } } \cdot \frac{\mathrm{ BQ } }{\mathrm{ QC } } \cdot \frac{\mathrm{ CE } }{\mathrm{ EA } } &=& 1 \\[5pt]
\frac{1}{3} \cdot \frac{\mathrm{ BQ } }{\mathrm{ CQ } } \cdot \frac{4}{1} &=& 1 \\[5pt]
\frac{\mathrm{ BQ } }{\mathrm{ CQ } } &=& \frac{3}{4} \\[5pt]
\end{eqnarray}となります。
$\mathrm{ BC }=7$ なので、 $\mathrm{ BQ }=3$ です。また、 $\mathrm{ BQ }=\mathrm{ BD }=3$ なので、三角形 ABC の内接円と BC は、点 Q で接することがわかります。なので、 $\mathrm{ IQ }$ は、内接円の半径と等しいので $\dfrac{\sqrt{6} }{2}$ となります。
解答
クケ:34
コ:3
サシ:62
解答編 つづき
問題
また、直線 CP と $\triangle \mathrm{ ABC }$ の内接円との交点で D とは異なる点を F とすると\[ \cos\angle \mathrm{ DFE }=\dfrac{\myBox{スセ} }{\myBox{ソ} } \]である。
解説
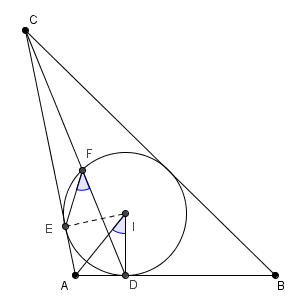
円周角の定理から、 $\angle \mathrm{ DFE }=\frac{1}{2}\angle \mathrm{ EID }$ です。なので、 $\angle \mathrm{ DFE }=\angle \mathrm{ DIA }$ です。 $\mathrm{ AD }=1$, $\mathrm{ ID }=\frac{\sqrt{6} }{2}$ であり、\[ \mathrm{ AI }=\sqrt{1+\left(\frac{\sqrt{6} }{2}\right)^2}=\frac{\sqrt{10} }{2} \]となるので、
\begin{eqnarray}
\cos\angle \mathrm{ DFE }
&=&
\cos\angle \mathrm{ AID } \\[5pt]
&=&
\frac{\mathrm{ ID } }{\mathrm{ AI } } \\[5pt]
&=&
\frac{\sqrt{6} }{2}\cdot\frac{2}{\sqrt{10} } \\[5pt]
&=&
\frac{\sqrt{15} }{5} \\[5pt]
\end{eqnarray}と求められます。
解答
スセソ:155





