センター試験数学I・数学A 2019年度第2問 [2] 解説

【必答問題】

問題編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ }}\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ }}$全国各地の気象台が観測した「ソメイヨシノ(桜の種類)の開花日」や、「モンシロチョウの初見日(初めて観測した日)」、「ツバメの初見日」などの日付を気象庁が発表している。気象庁発表の日付は普通の月日形式であるが、この問題では該当する年の1月1日を「1」とし、12月31日を「365」(うるう年の場合は「366」)とする「年間通し日」に変更している。例えば、2月3日は、1月31日の「31」に2月3日の3を加えた「34」となる。

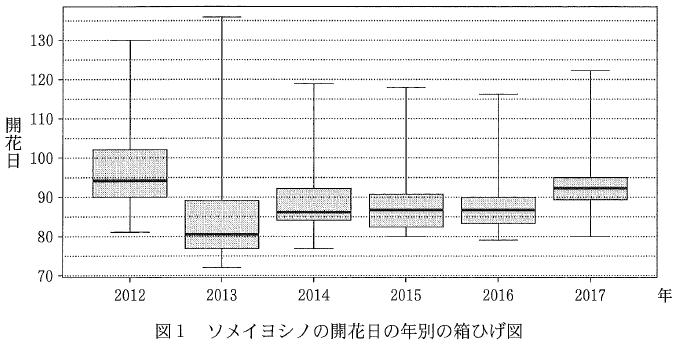
(1) 図1は全国48地点で観測しているソメイヨシノの2012年から2017年までの6年間の開花日を、年ごとに箱ひげ図にして並べたものである。

　図2はソメイヨシノの開花日の年ごとのヒストグラムである。ただし、順番は年の順に並んでいるとは限らない。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　次の $\mybox{ソ}$, $\mybox{タ}$ に当てはまるものを、図2の 0 ～ 5のうちから一つずつ選べ。

　・2013年のヒストグラムは $\mybox{ソ}$ である。
　・2017年のヒストグラムは $\mybox{タ}$ である。

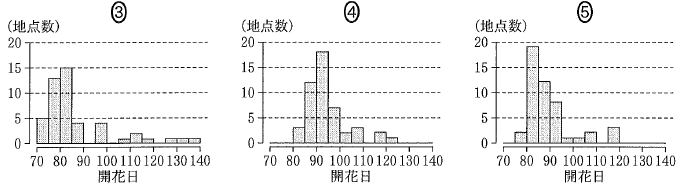
図2 ソメイヨシノの開花日の年別のヒストグラム

(出典：図1、図2は気象庁「生物季節観測データ」Webページにより作成)

(2) 図3 と図4 は、モンシロチョウとツバメの両方を観測している 41地点における、2017年の初見日の箱ひげ図と散布図である。散布図の点には重なった点が2点ある。なお、散布図には原点を通り傾き 1 の直線(実線)、切片が -15 および 15 で傾きが 1 の2本の直線(破線)を付加している。

　次の $\mybox{チ}$, $\mybox{ツ}$ に当てはまるものを、下の 0 ～ 7 のうちから一つずつ選べ。ただし、解答の順序は問わない。

　図3、図4 から読み取れることとして正しくないものは、 $\myBox{チ}$, $\myBox{ツ}$ である。

　0: モンシロチョウの初見日の最小値はツバメの初見日の最小値と同じである。
　1: モンシロチョウの初見日の最大値はツバメの初見日の最大値より大きい。

　2: モンシロチョウの初見日の中央値はツバメの初見日の中央値より大きい。
　3: モンシロチョウの初見日の四分位範囲はツバメの初見日の四分位範囲の3倍より小さい。

　4: モンシロチョウの初見日の四分位範囲は15日以下である。
　5: ツバメの初見日の四分位範囲は15日以下である。

　6: モンシロチョウとツバメの初見日が同じ所が少なくとも4地点ある。
　7: 同一地点でのモンシロチョウの初見日とツバメの初見日の差は15日以下である。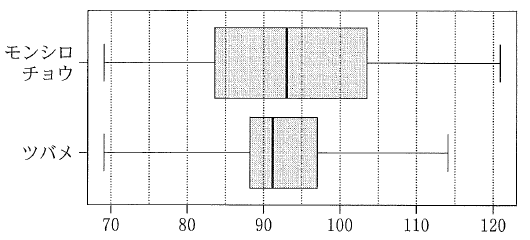

図3 モンシロチョウとツバメの初見日(2017年)の箱ひげ図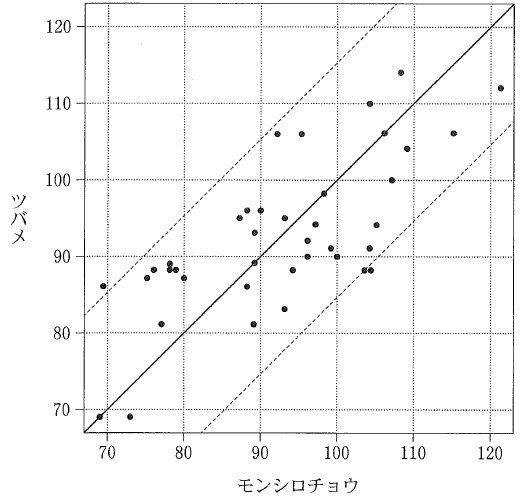

図4 モンシロチョウとツバメの初見日(2017年)の散布図

(出典：図3、図4は気象庁「生物季節観測データ」Webページにより作成)

(3) 一般に $n$ 個の数値 $x_1,x_2,\cdots,x_n$ からなるデータ $X$ の平均値を $\bar{x}$ 、分散を $s^2$ 、標準偏差を $s$ とする。各 $x_j$ に対して\[ x_i’=\frac{x_i-\bar{x}}{s}\ (i=1,2,\cdots ,n) \]と変換した $x_1′,x_2′,\cdots,x_n’$ をデータ $X’$ とする。ただし、 $x\geqq 2$, $s\gt 0$ とする。

　次の $\mybox{テ}$, $\mybox{ト}$, $\mybox{ナ}$ に当てはまるものを、下の 0 ～ 8 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　・ $X$ の偏差 $x_1-\bar{x}$, $x_2-\bar{x}$, $\cdots$, $x_n-\bar{x}$ の平均値は $\myBox{テ}$ である。
　・ $X’$ の平均値は $\myBox{ト}$ である。
　・ $X’$ の標準偏差は $\myBox{ナ}$ である。

　0: $0$
　1: $1$
　2: $-1$

　3: $\bar{x}$
　4: $s$

　5: $\dfrac{1}{s}$

　6: $s^2$

　7: $\dfrac{1}{s^2}$

　8: $\dfrac{\bar{x}}{s}$

　図4で示されたモンシロチョウの初見日のデータ $M$ とツバメの初見日のデータ $T$ について上の変換を行ったデータをそれぞれ $M’$, $T’$ とする。

　次の $\myBox{ニ}$ に当てはまるものを、図5の 0 ～ 3 のうちから一つ選べ。

　変換後のモンシロチョウの初見日のデータ $M’$ と変換後のツバメの初見日のデータ $T’$ の散布図は、 $M’$ と $T’$ の標準偏差の値を考慮すると $\myBox{ニ}$ である。

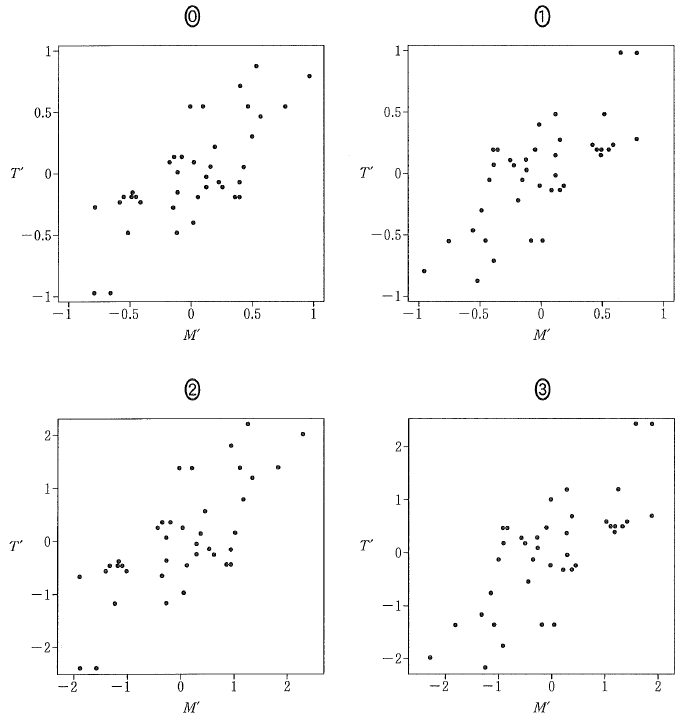
図5 四つの散布図