センター試験 数学I・数学A 2019年度 第1問 [3] 解説
【必答問題】
問題編
問題
$a$ と $b$ はともに正の実数とする。 $x$ の2次関数\[ y=x^2+(2a-b)x+a^2+1 \]のグラフを $G$ とする。
(1) グラフ $G$ の頂点の座標は\[ \left(\frac{b}{\myBox{チ} }-a, -\frac{b^2}{\myBox{ツ} }+ab+\myBox{テ}\right) \]である。
(2) グラフ $G$ が点 $(-1,6)$ を通るとき、 $b$ のとり得る値の最大値は $\myBox{ト}$ であり、そのときの $a$ の値は $\myBox{ナ}$ である。
$b=\mybox{ト}$, $a=\mybox{ナ}$ のとき、グラフ $G$ が2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\dfrac{\myBox{ニ} }{\myBox{ヌ} }$, $y$ 軸方向に $\dfrac{\myBox{ネノ} }{\myBox{ハ} }$ だけ平行移動したものである。
考え方
(1)は平方完成をするだけですが、文字が多いので慎重に計算しましょう。
(2)は、通る点の条件から、 $a,b$ の関係式を導きましょう。後半は、(1)で頂点を求めているので、これを利用して考えましょう。
【必答問題】
解答編
問題
$a$ と $b$ はともに正の実数とする。 $x$ の2次関数\[ y=x^2+(2a-b)x+a^2+1 \]のグラフを $G$ とする。
(1) グラフ $G$ の頂点の座標は\[ \left(\frac{b}{\myBox{チ} }-a, -\frac{b^2}{\myBox{ツ} }+ab+\myBox{テ}\right) \]である。
解説
平方完成をして
\begin{eqnarray}
y
&=&
x^2+(2a-b)x+a^2+1 \\[5pt]
&=&
\left(x+\frac{2a-b}{2}\right)^2-\frac{(2a-b)^2}{4}+a^2+1 \\[5pt]
&=&
\left(x-\frac{b-2a}{2}\right)^2-a^2+ab-\frac{b^2}{4}+a^2+1 \\[5pt]
&=&
\left\{x-\left(\frac{b}{2}-a\right)\right\}^2-\frac{b^2}{4}+ab+1 \\[5pt]
\end{eqnarray}となります。よって、頂点の座標は\[ \left(\frac{b}{2}-a, -\frac{b^2}{4}+ab+1\right) \]となります。
解答
チツテ:241
解答編 つづき
問題
(2) グラフ $G$ が点 $(-1,6)$ を通るとき、 $b$ のとり得る値の最大値は $\myBox{ト}$ であり、そのときの $a$ の値は $\myBox{ナ}$ である。
解答
グラフ $G$ が点 $(-1,6)$ を通るということは、 $x=-1$ を代入すると $y=6$ となる、ということなので、
\begin{eqnarray}
6 &=& (-1)^2+(2a-b)\cdot (-1)+a^2+1 \\[5pt]
6 &=& 1-2a+b+a^2+1 \\[5pt]
0 &=& a^2-2a-4+b \\[5pt]
\end{eqnarray}となります。よって、 $b=-a^2+2a+4$ となります。これを変形すると
\begin{eqnarray}
b=-(a-1)^2+5
\end{eqnarray}となり、 $a,b$ はともに正の実数という条件があるので、 $(a,b)$ のグラフは次のようになります。
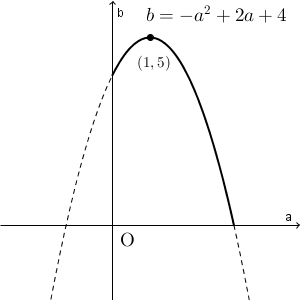
よって、 $b$ のとり得る値の最大値は $5$ で、そのときの $a$ の値は $1$ となることがわかります。
解答
トナ:51
解答編 つづき
問題
$b=\mybox{ト}$, $a=\mybox{ナ}$ のとき、グラフ $G$ が2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\dfrac{\myBox{ニ} }{\myBox{ヌ} }$, $y$ 軸方向に $\dfrac{\myBox{ネノ} }{\myBox{ハ} }$ だけ平行移動したものである。
解説
$b=5$, $a=1$ を、頂点の座標に代入してみましょう。
\begin{eqnarray}
& &
\left(\frac{b}{2}-a, -\frac{b^2}{4}+ab+1\right) \\[5pt]
&=&
\left(\frac{5}{2}-1, -\frac{5^2}{4}+1\cdot 5+1\right) \\[5pt]
&=&
\left(\frac{3}{2}, -\frac{1}{4}\right) \\[5pt]
\end{eqnarray}よって、頂点の移動で考えれば、このときのグラフ $G$ は、 $y=x^2$ のグラフを、 $x$ 軸方向に $\dfrac{3}{2}$, $y$ 軸方向に $\dfrac{-1}{4}$ 平行移動したものであることがわかります。
解答
ニヌ:32
ネノハ:-14





