センター試験 数学I・数学A 2019年度 第2問 [1] 解説
【必答問題】
問題編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=3$, $\mathrm{ BC }=4$, $\mathrm{ AC }=2$ とする。
次の $\mybox{エ}$ には、下の 0 ~ 2 のうちから当てはまるものを一つ選べ。$\cos\angle \mathrm{ BAC }=\dfrac{\myBox{アイ} }{\myBox{ウ} }$ であり、 $\angle \mathrm{ BAC }$ は $\myBox{エ}$ である。また、 $\sin\angle \mathrm{ BAC }=\dfrac{\sqrt{\myBox{オカ} }}{\myBox{キ} }$ である。
0: 鋭角
1: 直角
2: 鈍角
線分 AC の垂直二等分線と直線 AB の交点を D とする。
$\cos\angle \mathrm{ CAD }=\dfrac{\myBox{ク} }{\myBox{ケ} }$ であるから、 $\mathrm{ AD }=\myBox{コ}$ であり、 $\triangle \mathrm{ DBC }$ の面積は $\dfrac{\myBox{サ}\sqrt{\myBox{シス} }}{\myBox{セ} }$ である。
考え方
前半は、余弦定理や相互関係を用いる問題です。
後半は、図が正しく描けないと先に進めません。図をかくには、前半の問題がヒントになっています。 AD は、計算ではなく、図から読み取ります。最後の面積も、どのように考えるかで複雑さが変わってきますが、前半の結果を利用して解くのが一番簡単です。
ヒントは文中にありますが、どう利用するかはちょっと考えないといけません。
解答編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=3$, $\mathrm{ BC }=4$, $\mathrm{ AC }=2$ とする。
次の $\mybox{エ}$ には、下の 0 ~ 2 のうちから当てはまるものを一つ選べ。$\cos\angle \mathrm{ BAC }=\dfrac{\myBox{アイ} }{\myBox{ウ} }$ であり、 $\angle \mathrm{ BAC }$ は $\myBox{エ}$ である。また、 $\sin\angle \mathrm{ BAC }=\dfrac{\sqrt{\myBox{オカ} }}{\myBox{キ} }$ である。
0: 鋭角
1: 直角
2: 鈍角
解説
余弦定理から
\begin{eqnarray}
\cos\angle \mathrm{ BAC }
&=&
\frac{\mathrm{ BA }^2+\mathrm{ AC }^2-\mathrm{ BC }^2}{2\cdot \mathrm{ BA }\cdot \mathrm{ AC } } \\[5pt]
&=&
\frac{3^2+2^2-4^2}{2\cdot 3\cdot 2} \\[5pt]
&=&
\frac{-1}{4} \\[5pt]
\end{eqnarray}となります。 $\cos$ の値が負なので、 $\angle \mathrm{ BAC }$ は鈍角となります。
また、相互関係から
\begin{eqnarray}
\sin^2 \angle \mathrm{ BAC }
&=&
1-\cos^2 \angle \mathrm{ BAC } \\[5pt]
&=&
\frac{15}{16} \\[5pt]
\end{eqnarray}となるので、 $\sin\angle \mathrm{ BAC }=\frac{\sqrt{15} }{4}$ となります。
解答
アイウ:-14
エ:2
オカキ:154
解答編 つづき
問題
線分 AC の垂直二等分線と直線 AB の交点を D とする。
$\cos\angle \mathrm{ CAD }=\dfrac{\myBox{ク} }{\myBox{ケ} }$ であるから、 $\mathrm{ AD }=\myBox{コ}$ であり、 $\triangle \mathrm{ DBC }$ の面積は $\dfrac{\myBox{サ}\sqrt{\myBox{シス} }}{\myBox{セ} }$ である。
解説
図は次のようになります。 AC の中点を E としています。 $\angle \mathrm{ BAC }$ が鈍角なので、点 D は、線分 AB を A 側に伸ばした直線上にあります。
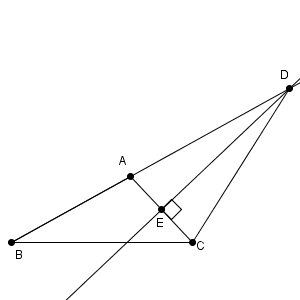
$\angle \mathrm{ BAC }+\angle \mathrm{ CAD }=180^{\circ}$ なので、\[ \cos \angle \mathrm{ CAD }=-\cos\angle \mathrm{ BAC }=\frac{1}{4} \]となります。
また、三角形ADE は直角三角形で $\mathrm{ AE }=1$ だから、先ほど求めた $\cos \angle \mathrm{ CAD }=\dfrac{1}{4}$ より、 $\mathrm{ AD }=4$ となることがわかります。
また、三角形DBC の面積は、三角形ABC と三角形ACD の面積の和だと考えて求めます。 $\sin \angle \mathrm{ CAD }=\sin\angle \mathrm{ BAC }$ であることも利用して、
\begin{eqnarray}
& &
\frac{1}{2}\mathrm{ AB }\cdot \mathrm{ AC }\sin\angle \mathrm{ BAC }
+\frac{1}{2}\mathrm{ AD }\cdot \mathrm{ AC }\sin\angle \mathrm{ CAD } \\[5pt]
&=&
\frac{\mathrm{ AC }\sin\angle \mathrm{ BAC } }{2} (\mathrm{ AB }+\mathrm{ AD }) \\[5pt]
&=&
2\cdot\frac{\sqrt{15} }{4}\cdot\frac{1}{2}\cdot (3+4) \\[5pt]
&=&
\frac{7\sqrt{15} }{4} \\[5pt]
\end{eqnarray}となります。
解答
クケ:14
コ:4
サシスセ:7154





