センター試験 数学I・数学A 2016年度追試 第2問 [3] 解説
問題編
問題
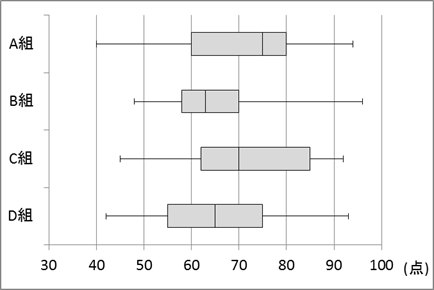
(注:一部表記を調整しています)A組からD組の各組30人の生徒に対して理科のテストを行った。次の図1は、各組ごとに理科のテストの得点を箱ひげ図にしたものである。
図1 A組からD組の理科のテストの箱ひげ図 (1) 次の $\mybox{シ}$, $\mybox{ス}$ に当てはまるものを、下の 0 ~ 5 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図1の箱ひげ図について述べた文として誤っているものは $\myBox{シ}$ と $\myBox{ス}$ である。
0: A, B, C, Dの4組全体の最高点の生徒がいるのはB組である。
1: A, B, C, Dの4組で比べたとき、四分位範囲が最も大きいのはA組である。
2: A, B, C, Dの4組で比べたとき、範囲が最も大きいのはA組である。
3: A, B, C, Dの4組で比べたとき、第1四分位数と中央値の差が最も小さいのはB組である。
4: A組では、60点未満の人数は80点以上の人数よりも多い。
5: A組とC組で70点以下の人数を比べたとき、C組の人数はA組の人数以上である。(2) 次の $\mybox{セ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
図1のC組の箱ひげ図のもとになった得点をヒストグラムにしたとき、対応するものは $\myBox{セ}$ である。ただし、ヒストグラムは [2] の表2の度数分布表と同じ階級を用いて作成した。
0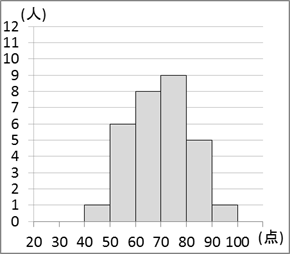
1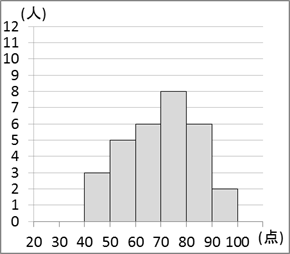
2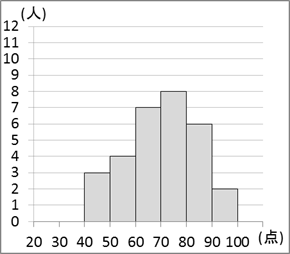
3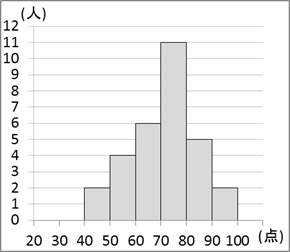
考え方
(1)は面倒ですが、1個1個チェックしていくしかありません。箱ひげ図が何を表しているかを考えて読み取れば、それほど難しくはないでしょう。
(2)も面倒ですが、1個1個チェックしていきます。四分位数で矛盾がないかをチェックしていくと答えが見つかりやすいです。
解答編
問題
(注:一部表記を調整しています)
A組からD組の各組30人の生徒に対して理科のテストを行った。次の図1は、各組ごとに理科のテストの得点を箱ひげ図にしたものである。
図1 A組からD組の理科のテストの箱ひげ図 (1) 次の $\mybox{シ}$, $\mybox{ス}$ に当てはまるものを、下の 0 ~ 5 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図1の箱ひげ図について述べた文として誤っているものは $\myBox{シ}$ と $\myBox{ス}$ である。
0: A, B, C, Dの4組全体の最高点の生徒がいるのはB組である。
1: A, B, C, Dの4組で比べたとき、四分位範囲が最も大きいのはA組である。
2: A, B, C, Dの4組で比べたとき、範囲が最も大きいのはA組である。
3: A, B, C, Dの4組で比べたとき、第1四分位数と中央値の差が最も小さいのはB組である。
4: A組では、60点未満の人数は80点以上の人数よりも多い。
5: A組とC組で70点以下の人数を比べたとき、C組の人数はA組の人数以上である。
解説
各選択肢が正しいか間違っているかを順番に見ていきます。
0 の「A, B, C, Dの4組全体の最高点の生徒がいるのはB組である。」について。
最高点は箱ひげ図の右端を見ればわかります。一番右までグラフが伸びているのはB組なので、B組に最高点の生徒がいることがわかります。正しいですね。
1の「A, B, C, Dの4組で比べたとき、四分位範囲が最も大きいのはA組である。」について。
四分位範囲とは、箱の長さのことです。A組の四分位範囲は20点ですが、C組の四分位範囲はあきらかに20点以上あります。なので、最も大きいのがA組とは言えません。誤りです。
2の「A, B, C, Dの4組で比べたとき、範囲が最も大きいのはA組である。」について。
範囲とは、箱ひげ図の長さのことです。一番右から一番左までですね。A組と比較すると、C組・D組は最小値が大きく、最大値が小さいため、範囲は小さくなります。
B組の最大値・最小値は、A組の最大値・最小値よりも大きいです。しかし、A組とB組の最大値の差に比べ、A組とB組の最小値の差の方が大きいことがわかります。そのため、A組の範囲の方が大きくなります。
以上から、範囲が最も大きいのはA組であることがわかります。正しいです。
3の「A, B, C, Dの4組で比べたとき、第1四分位数と中央値の差が最も小さいのはB組である。」について。
第1四分位数とは箱の左端、中央値は箱の真ん中にある線のことですね。B組はこの差が5点程度ですが、他はもっと広いですね。そのため、差が最も小さいのはB組です。正しいです。
4の「A組では、60点未満の人数は80点以上の人数よりも多い。」について。
箱ひげ図から、A組の第1四分位数が60点、第3四分位数が80点であることがわかります。
クラスは30人なので、第1四分位数は下位15人の中央値、つまり、下から8番目です。そのため、60点未満の人は、7人以下となります。(下位7人の中に60点の人がいるかもしれないので、「7人」ではなく「7人以下」です)
一方、第3四分位数は上位15人の中央値なので、上から8番目です。そのため、80点以上の人は、8人以上となります。
以上から、「60点未満の人数は80点以上の人数よりも多い」とはなりません。誤りです。
5の「A組とC組で70点以下の人数を比べたとき、C組の人数はA組の人数以上である。」について。
C組の中央値が70点なので、70点以下の人数は15人以上であるため、15人を下回ることはありません。一方、A組の中央値は70点より高いので、70点以下の人数は最大でも15人です。なので、「C組の人数はA組の人数以上」となります。正しいです。
以上から、誤っているものは、1と4であることがわかります。
解答
シス:1,4
参考
解答編 つづき
問題
(2) 次の $\mybox{セ}$ に当てはまるものを、下の 0 ~ 3 のうちから一つ選べ。
図1のC組の箱ひげ図のもとになった得点をヒストグラムにしたとき、対応するものは $\myBox{セ}$ である。ただし、ヒストグラムは [2] の表2の度数分布表と同じ階級を用いて作成した。
0
1
2
3
解説
C組の箱ひげ図と矛盾するものを捨てていく、という方針で考えていきます。
まず、最大値は90点台、最小値は40点台ですが、これと矛盾するヒストグラムはありません。
中央値は70点、第1四分位数は60点台、第3四分位数は80点台です。このクラスの生徒数は30人なので、中央値は「上から15番目と16番目の平均」、第1四分位数は「下から8番目」、第3四分位数は「上から8番目」となります。これらを用いて、ヒストグラムを見ていきましょう。
0も3も、上から8番目が70点台なので、第3四分位数があいません。1は、下から8番目が50点台なので、第1四分位数があいません。一方、2は、上から8番目が80点台、下から8番目が60点台です。上から15番目と16番目はともに70点台なので、この平均も70点台で矛盾しません。
以上より、2が正解となります。
解答
セ:2