センター試験 数学I・数学A 2016年度追試 第2問 [1] 解説
問題編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=1$, $\mathrm{ CA }=\sqrt{3}$, $\displaystyle \cos\angle \mathrm{ BAC }=-\frac{\sqrt{3} }{3}$ とすると、 $\mathrm{ BC }=\sqrt{\myBox{ア}}$ であり、 $\triangle \mathrm{ ABC }$ の面積は $\displaystyle \frac{\sqrt{\myBox{イ}} }{\myBox{ウ}}$ である。
$\triangle \mathrm{ ABC }$ の外接円の中心を O とし、直線 OB と $\triangle \mathrm{ ABC }$ の外接円との交点で B と異なる点を D とすると、 $\mathrm{ BD }=\myBox{エ}$ であり、 $\triangle \mathrm{ BCD }$ の面積は $\displaystyle \frac{\myBox{オ}\sqrt{\myBox{カ}} }{\myBox{キ}}$ である。
直線 AD と直線 BC との交点を E とすると
\begin{eqnarray} \frac{\mathrm{ AE } }{\mathrm{ DE } } = \frac{\myBox{ク}}{\myBox{ケ}} \end{eqnarray}である。
考え方
前半は、余弦定理や相互関係を使って解く基本的な問題です。
中盤は、直径や直角が出てきていることに注目して解いていきます。
最後は、ここまでの流れを踏まえて考えるか、相似な三角形に注目して解きましょう。
解答編
問題
$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=1$, $\mathrm{ CA }=\sqrt{3}$, $\displaystyle \cos\angle \mathrm{ BAC }=-\frac{\sqrt{3} }{3}$ とすると、 $\mathrm{ BC }=\sqrt{\myBox{ア}}$ であり、 $\triangle \mathrm{ ABC }$ の面積は $\displaystyle \frac{\sqrt{\myBox{イ}} }{\myBox{ウ}}$ である。
解説

余弦定理より
\begin{eqnarray}
\mathrm{ BC }^2
&=&
\mathrm{ CA }^2+\mathrm{ AB }^2 -2\mathrm{ CA }\cdot\mathrm{ AB }\cos\angle \mathrm{ BAC } \\[5pt]
&=&
3+1 -2\sqrt{3} \times \left(-\frac{\sqrt{3} }{3}\right) \\[5pt]
&=&
4 +2 \\[5pt]
&=&
6 \\[5pt]
\end{eqnarray}なので、 $\mathrm{ BC }=\sqrt{6}$ となります。
三角比の相互関係から
\begin{eqnarray}
\sin\angle \mathrm{ BAC }
&=&
\sqrt{1-\cos^2 \angle \mathrm{ BAC } } \\[5pt]
&=&
\sqrt{1-\left(-\frac{\sqrt{3} }{3}\right)^2} \\[5pt]
&=&
\frac{\sqrt{6} }{3} \\[5pt]
\end{eqnarray}なので、 $\triangle \mathrm{ ABC }$ の面積は次のように求められます。
\begin{eqnarray}
& &
\frac{1}{2}\times\mathrm{ AB }\cdot\mathrm{ AC }\cdot\sin\angle \mathrm{ BAC } \\[5pt]
&=&
\frac{1}{2} \times \sqrt{3} \times \frac{\sqrt{6} }{3} \\[5pt]
&=&
\frac{\sqrt{2} }{2}
\end{eqnarray}
解答
ア:6イウ:22
参考
解答編 つづき
問題
$\triangle \mathrm{ ABC }$ の外接円の中心を O とし、直線 OB と $\triangle \mathrm{ ABC }$ の外接円との交点で B と異なる点を D とすると、 $\mathrm{ BD }=\myBox{エ}$ であり、 $\triangle \mathrm{ BCD }$ の面積は $\displaystyle \frac{\myBox{オ}\sqrt{\myBox{カ}} }{\myBox{キ}}$ である。
解説

BD は $\triangle \mathrm{ ABC }$ の外接円の直径です。これは、正弦定理から次のように求めることができます。
\begin{eqnarray}
\frac{\mathrm{ BC } }{\sin\angle\mathrm{ BAC } }
&=&
\sqrt{6} \times \frac{3}{\sqrt{6} } \\[5pt]
&=&
3
\end{eqnarray}
$\angle \mathrm{ BCD }=90^{\circ}$ なので、三平方の定理から
\begin{eqnarray}
\mathrm{ CD }=\sqrt{3^2-(\sqrt{6})^2}=\sqrt{3}
\end{eqnarray}が得られます。よって、 $\triangle \mathrm{ BCD }$ の面積は
\begin{eqnarray}
\frac{1}{2} \times \mathrm{ BC }\cdot\mathrm{ CD }=\frac{3\sqrt{2} }{2}
\end{eqnarray}となります。
解答
エ:3
オカキ:322
参考
解答編 つづき
問題
直線 AD と直線 BC との交点を E とすると
\begin{eqnarray} \frac{\mathrm{ AE } }{\mathrm{ DE } } = \frac{\myBox{ク}}{\myBox{ケ}} \end{eqnarray}である。
解説
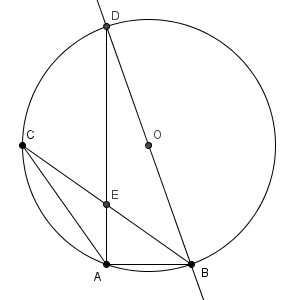
まずは、ここまでの流れを踏まえて解いてみます。
$\mathrm{B}$ から $\mathrm{AD}$ に垂線をおろすと、線分 $\mathrm{AE}$ と線分 $\mathrm{DE}$ の長さの比は、三角形 $\mathrm{ABE}$ と三角形 $\mathrm{DBE}$ の面積比と等しいことがわかります。
また、 $\mathrm{C}$ から $\mathrm{AD}$ に垂線をおろすと、線分 $\mathrm{AE}$ と線分 $\mathrm{DE}$ の長さの比は、三角形 $\mathrm{ACE}$ と三角形 $\mathrm{DCE}$ の面積比と等しいことがわかります。
よって、線分 $\mathrm{AE}$ と線分 $\mathrm{DE}$ の長さの比は、三角形 $\mathrm{ABC}$ と三角形 $\mathrm{BCD}$ の面積比と等しいです。この2つの面積はすでに求めているので
\begin{eqnarray}
\frac{\mathrm{AE}}{\mathrm{DE}}=\frac{\sqrt{2}}{2} \div \frac{3\sqrt{2}}{2} =\frac{1}{3}
\end{eqnarray}となります。

相似を利用して解くこともできます。 $\triangle \mathrm{ ACE }$ と $\triangle \mathrm{ BDE }$ は相似です。また、\[ \mathrm{ AC }:\mathrm{ BD }=\sqrt{3}:3=1:\sqrt{3} \]です。なので、 $\mathrm{ AE }=x$ とすると、 $\mathrm{ BE }=\sqrt{3}x$ となります。また、 BD は直径なので、 $\angle \mathrm{ EAB }$ は直角です。よって、三平方の定理から
\begin{eqnarray}
\mathrm{ AB }^2+\mathrm{ AE }^2 &=& \mathrm{ BE }^2 \\
1+x^2 &=& 3x^2 \\
x^2 &=& \frac{1}{2} \\
\end{eqnarray}が得られます。これより、 $\displaystyle \mathrm{ AE }=x=\frac{\sqrt{2} }{2}$ が得られます。
$\triangle \mathrm{ ABD }$ も直角三角形なので、三平方の定理から
\begin{eqnarray}
\mathrm{ AD }^2
&=&
\sqrt{\mathrm{ BD }^2-\mathrm{ AB }^2} \\
&=&
\sqrt{3^2-1^2}=2\sqrt{2}
\end{eqnarray}が得られます。よって、
\begin{eqnarray}
\mathrm{ DE }
&=&
\mathrm{ AD }-\mathrm{ AE } \\[5pt]
&=&
2\sqrt{2}-\frac{\sqrt{2} }{2}=\frac{3\sqrt{2} }{2}
\end{eqnarray}なので、
\begin{eqnarray}
\frac{\mathrm{ AE } }{\mathrm{ DE } } = \frac{\sqrt{2} }{2} \div \frac{ 3\sqrt{2} }{ 2 } =\frac{1}{3}
\end{eqnarray}となります。
解答
クケ:13





