センター試験 数学I・数学A 2016年度追試 第1問 [3] 解説
問題編
問題
a, b は定数で、 $a\ne 0$ とする。 x の2次関数\[ y=a^2x^2-4ax+b \quad \cdots ① \]を考える。①のグラフの頂点の x 座標が1以上3以下になるような a の値の範囲は $\displaystyle \frac{\myBox{サ}}{\myBox{シ}} \leqq a \leqq \myBox{ス}$ である。
下の $\mybox{セ}$ には、次の 0 ~ 4 のうちから当てはまるものを一つ選べ。
0: $\gt$
1: $\lt$
2: $\geqq$
3: $\leqq$
4: $\ne$x の2次不等式\[ a^2x^2-4ax+b \lt 0 \quad \cdots ② \]の解が存在するような b の値の範囲は
$b\ \myBox{セ}\ \myBox{ソ}$
である。また②の解が $1\lt x \lt 3$ になるような a, b の値は
$a=\myBox{タ}$, $b=\myBox{チ}$
である。
考え方
前半は、頂点に関する条件を考えるので、平方完成すればいいですね。文字が入っていて計算しづらいですが、落ち着いて計算しましょう。
中盤は判別式を用いてもいいですが、先ほどの平方完成の結果を使う方が早いでしょう。
最後はグラフをかいて考えると、どういう条件が答えになるかがわかりやすくなります。
解答編
問題
a, b は定数で、 $a\ne 0$ とする。 x の2次関数\[ y=a^2x^2-4ax+b \quad \cdots ① \]を考える。①のグラフの頂点の x 座標が1以上3以下になるような a の値の範囲は $\displaystyle \frac{\myBox{サ}}{\myBox{シ}} \leqq a \leqq \myBox{ス}$ である。
解説
まずは頂点を求めるために平方完成をします。
\begin{eqnarray}
y
&=&
a^2x^2-4ax+b \\[5pt]
&=&
a^2\left(x^2-\frac{4}{a}x\right)+b \\[5pt]
&=&
a^2\left(x^2-\frac{4}{a}x+\frac{4}{a^2}-\frac{4}{a^2}\right)+b \\[5pt]
&=&
a^2\left(x-\frac{2}{a}\right)^2 -4+b \\[5pt]
\end{eqnarray}これから、頂点の x 座標が $\displaystyle \frac{2}{a}$ になることがわかります。これが1以上3以下になる範囲を考えます。このとき a は正でないといけないので、次のように変形できます。
\begin{eqnarray}
1 & \leqq \frac{2}{a} \leqq 3 \\[5pt]
a & \leqq 2 \leqq 3a \\[5pt]
\end{eqnarray}左の不等式から、 $a\leqq 2$ となり、右の不等式から $\displaystyle \frac{2}{3}\leqq a$ が得られます。この2つの共有部分が解なので、求める範囲は\[ \frac{2}{3} \leqq a \leqq 2 \] となります。
解答
サシス:233
参考
解答編 つづき
問題
下の $\mybox{セ}$ には、次の 0 ~ 4 のうちから当てはまるものを一つ選べ。
0: $\gt$
1: $\lt$
2: $\geqq$
3: $\leqq$
4: $\ne$x の2次不等式\[ a^2x^2-4ax+b \lt 0 \quad \cdots ② \]の解が存在するような b の値の範囲は
$b\ \myBox{セ}\ \myBox{ソ}$
である。
解説
先ほどの平方完成の結果から、 $y=a^2x^2-4ax+b$ の頂点は $\left(\frac{a}{2},b-4\right)$ であることがわかります。2次不等式 $a^2x^2-4ax+b \lt 0$ の解が存在するときというのは、この頂点の y 座標が負であればいいので $b-4\lt 0$ 、つまり、\[ b\lt 4 \]のときであることがわかります。
解答
セソ:14
解答編 つづき
問題
また②の解が $1\lt x \lt 3$ になるような a, b の値は
$a=\myBox{タ}$, $b=\myBox{チ}$
である。
解説
$a^2x^2-4ax+b \lt 0$ の解が $1\lt x \lt 3$ となるとき、グラフは次のようになっています。
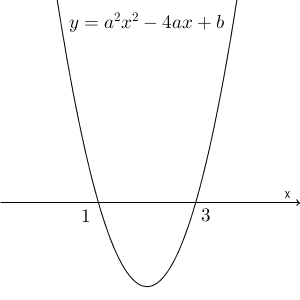
$x=1,3$ を代入したときに、関数の値は0となります。
$x=1$ の場合を考えると $a^2-4a+b=0$ となり、 $x=3$ のときを考えると $9a^2-12a+b=0$ となります。辺々引くと、次のようになります。
\begin{eqnarray}
(a^2-4a)-(9a^2-12a) &=& 0 \\
-8a^2+8a &=& 0 \\
a(a-1) &=& 0 \\
\end{eqnarray}ここで、 $a\ne 0$ なので、 $a=1$ が得られます。この結果を代入すれば
\begin{eqnarray}
1-4+b &=& 0 \\
b &=& 3 \\
\end{eqnarray}が得られます。
解答
タチ:13





