【標準】指数関数の逆関数

🕒 2018/07/11 🔄 2023/06/22

ここでは、今まで扱ったことのある指数関数を用いて、逆関数について考えていきたいと思います。

📘 目次

指数関数の逆関数

指数関数 $y=2^x$ について、この逆関数がどうなるかを考えてみましょう。

逆関数を求めるには、まずは「 $x=$ 」の形に変形すればいいのでした（参考：【基本】逆関数の定義域と値域）。この指数関数を「 $x=$ 」の形に変形するためには、底が $2$ の対数を考えればいいですね。\[ x=\log_2 y \]となります。よって、この指数関数 $y=2^x$ の逆関数は $y=\log_2 x$ となります。2つのグラフをかくと、次のようになります。

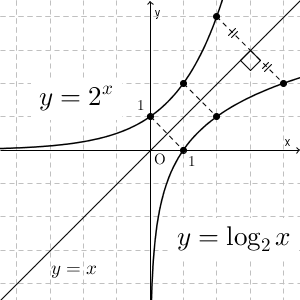
【基本】逆関数のグラフで見たように、直線 $y=x$ について対称になっていますね。

一般に、 $a\gt 0, a\ne 1$ のとき、実数 $x$ と正の実数 $y$ について、 $y=a^x$ が成り立つことと $x=\log_a y$ が成り立つことは同値です。そのため、指数関数 $y=a^x$ の逆関数は対数関数 $y=\log_a x$ であり、対数関数 $y=\log_a x$ の逆関数は指数関数 $y=a^x$ となります。

グラフをかいてみましょう。 $a\gt 1$ のときは、2つのグラフの形は、 $y=2^x$ のときとほとんどかわりません。一方、 $0\lt a \lt 1$ のときは、こうなります。

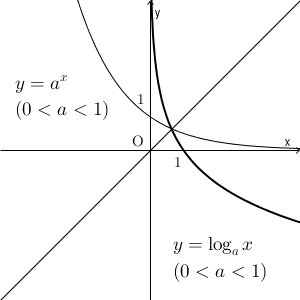
直線 $y=x$ について対称になっていることがわかります。

対数関数の逆関数

先ほども書きましたが、対数関数の逆関数は指数関数になります。ここでは、\[ y=\log_3(x-2)-1 \]という関数の逆関数を求めてみましょう。

これは\[ \log_3 (x-2)=y+1 \]と変形できるため、両辺の $3$ 乗を考えて\[ x-2=3^{y+1} \]となることがわかります。これより、 $x=3^{y+1}+2$ となることがわかるので、逆関数は\[ y=3^{x+1}+2 \]となります。

対数の定義が使えない場合

上の2つの例では、 $y=a^x$ が成り立つことと $x=\log_a y$ が成り立つことが同値であることを利用した式変形を行っています。しかし、こうした対数の定義に基づいた変形ができないケースもあります。

例題

$y=3^x-3^{-x}$ の逆関数を求めなさい。

これは、底を $3$ とする対数を考えてもあまり意味がありません。 $\log_3(3^x-3^{-x})$ は、これ以上変形できません。対数の差は真数の商になりますが、今のケースでは真数の差ですからね。これ以上はどうすることもできず、「 $x=$ 」の形に変形できません。

しかし、両辺に $3^x$ を掛けて、 $t=3^x$ とおいて、 $t$ の2次方程式だと考えれば、「 $t=$ 」から始まる式が得られ、「 $x=$ 」から始まる式も得られます。

両辺に $3^x$ を掛けると、\[ (3^x)^2-y\cdot 3^x-1=0 \]となります。 $t=3^x$ と置けば、この2次方程式は $t^2-yt-1=0$ なので\[ t=\frac{y\pm\sqrt{y^2+4} }{2} \]となります。ここで、\[ y^2 \lt y^2+4 \]なので、 $y$ がどんな値でも、 $y+\sqrt{y^2+4}$ は正であり、 $y-\sqrt{y^2+4}$ は負です。一方、 $t=3^x$ だったので、 $t$ は正です。そのため、\[ t=\frac{y+\sqrt{y^2+4} }{2} \]であることがわかり、 $t=3^x$ だったので、\[
x=\log_3 \frac{y+\sqrt{y^2+4} }{2} \]となることがわかります。

以上から、逆関数は、\[ y=\log_3 \frac{x+\sqrt{x^2+4} }{2} \]となります。

このように、簡単には「 $x=$ 」の形に変形できない場合もあります。