【標準】偶関数と奇関数の定積分

ここでは、偶関数と奇関数について紹介し、それらの定積分について見ていきます。

自然数乗の定積分をもう一度考えてみる

【基本】偶数乗と奇数乗の定積分で見たように、 $n$ が自然数のとき、
\begin{eqnarray} \int_{-a}^a x^{2n} dx &=& 2\int_0^a x^{2n} dx \\[5pt] \int_{-a}^a x^{2n-1} dx &=& 0 \\[5pt] \end{eqnarray}が成り立つのでした。このことについて、グラフを使って考えてみましょう。

【基本】定積分の復習でも見ましたが、定積分は面積を求めていることになります。例えば、\[ \int_{-1}^1 x^2 dx \]は、次の青い部分の面積が求められています。

$y=x^2$ と $x=-1$, $x=1$, $x$ 軸で囲まれた部分の面積を計算していることになります。これを見ると、 $y=x^2$ は $y$ 軸について対称なのだから、右半分を2倍すれば全体の面積になることはわかりますね。上で見た\[ \int_{-a}^a x^{2n} dx = 2\int_0^a x^{2n} dx \]はまさにこのことを表しています。左辺が全体の面積に、右辺が右半分の面積を2倍したものに、それぞれ対応しているわけです。

では、奇数乗はどうなるかを考えてみましょう。\[ \int_{-1}^1 x^3 dx \]の場合を考えてみましょう。

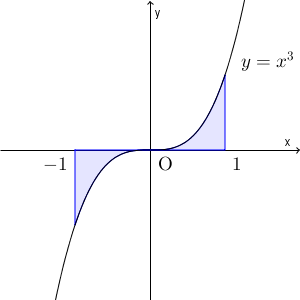
今回は先ほどと異なり、左側の部分が $x$ 軸より下側にあります。このような場合、正しく面積を求めるには、 $x^3$ ではなく、 $|x^3|$ を積分しなくてはいけません（参考：【基本】絶対値のついた関数の定積分の復習）。絶対値をつけずに計算すると、実際の面積にマイナスがついたものが計算されてしまいます。

つまり、\[ \int_{-1}^0 x^3 dx \]は、 $y=x^3$ と $x=-1$ と $x$ 軸で囲まれた部分の面積を $-1$ 倍したものになります。 $y=x^3$ は原点について対称なので、左側の部分と右側の部分の面積が同じだから、結局\[ \int_{-1}^0 x^3 dx+\int_0^1 x^3 dx=0 \]となるんですね。上で見た\[ \int_{-a}^a x^{2n-1} dx = 0 \]はこの「右側と左側が打ち消し合って $0$ になってしまうこと」を表しています。

つまり、グラフが $y$ 軸について対称の場合は、 $y$ 軸より右側の部分を2倍すればいい、原点について対称な場合は打ち消し合って $0$ になる、ということだったわけです。

偶関数と奇関数の定積分

先ほど見た通り、\[ \int_{-a}^a x^n dx \]が簡単に計算できるのは、グラフが $y$ 軸について対称となっていること、原点について対称となっていることがキーになっていることがわかりました。

グラフがこれらの性質をもつような関数は、 $x^n$ 以外にもありますね。例えば、 $y=\cos x$ のグラフは、 $y$ 軸について対称です。 $y=\sin x$ は、原点について対称ですね。

このように、 $y=f(x)$ のグラフが $y$ 軸について対称となる場合、式で書くと\[ f(x)=f(-x) \]が常に成り立つ場合、 $f(x)$ を偶関数(even function) といいます。

一方、グラフが原点について対称となる場合、式で書くと\[ f(x)=-f(-x) \]が常に成り立つ場合、 $f(x)$ を奇関数(odd function) といいます。

それぞれ、偶数乗・奇数乗と似た性質を持っているので、偶・奇の名前がついている、と考えれば覚えやすいでしょう。

偶関数や奇関数の場合に、\[ \int_{-a}^a f(x) dx \]を計算してみましょう。既に予想できると思いますが、偶数乗や奇数乗の定積分と似た性質が得られます。

【基本】偶数乗と奇数乗の定積分で見たように、 $x=-t$ として、置換積分を使いましょう。
\begin{eqnarray} & & \int_{-a}^a f(x) dx \\[5pt] &=& \int_{-a}^0 f(x) dx+\int_0^a f(x) dx \\[5pt] &=& \int_a^0 f(-t) \cdot(-1)dt+\int_0^a f(x) dx \\[5pt] &=& \int_0^a f(-t) dt+\int_0^a f(x) dx \\[5pt] \end{eqnarray}となります。ここで、 $f(x)$ が偶関数の場合は、 $f(-t)=f(t)$ なのだから、最後の式は、 $2\int_0^a f(x) dx$ となることがわかります。一方、 $f(x)$ が奇関数の場合は、 $f(-t)=-f(t)$ なのだから、最後の式は $0$ となることがわかります。

まとめると、次のようになります。

面積で考えれば、偶関数の場合はグラフが $y$ 軸について対称なので、 $y$ 軸より右の部分の面積を2倍すればいい、ということですね。奇関数の場合は、グラフが原点について対称なので、左側の積分は右側の面積の $-1$ 倍となり、打ち消し合って $0$ になるわけですね。

これらのことを使えば、例えば\[ \int_{-\pi}^{\pi} \sin^3 x dx \]というのは、 $\sin^3(-x)=-\sin^3 x$ で奇関数だとわかるから、すぐに $0$ だとわかります。

おわりに

ここでは、偶関数・奇関数の定積分について考えました。 $-a$ から $a$ まで、といった積分区間の場合には、偶関数は $0$ から $a$ までの定積分を2倍すればいいし、奇関数の場合は $0$ になることを見ました。特に、奇関数の場合には消えてなくなるので、かなりステキですね。