🏠 Home / 数学III / 積分 / 定積分

【基本】絶対値のついた関数の定積分の復習

🕒 2018/11/27 🔄 2023/05/01

ここでは、絶対値のついた関数の定積分の計算を振り返っていきます。計算の仕方は、以前学んだときと同じです。

📘 目次

絶対値のついた関数の定積分

例題

次の定積分を計算しなさい。\[ \int_0^{\pi} |\cos x| dx \]

絶対値がついている問題は、まず「絶対値を外せないかな」と考えるのが王道です。

今の場合、 $\cos x$ は正の値も負の値も取りうるので、そのまま外すことはできません。しかし、積分区間を次のように分解してみましょう。\[ \int_0^{\pi} |\cos x| dx=\int_0^{\frac{\pi}{2} } |\cos x| dx+\int_{\frac{\pi}{2} }^{\pi} |\cos x| dx \]ここでは、【基本】定積分の復習で見た、積分区間に関する性質を使っています。

さて、右辺の前半部分は、「微分して $|\cos x|$ になるもの」ですが、ここで考えている範囲は $0\leqq x\leqq \frac{\pi}{2}$ なので、「微分して $\cos x$ になるもの」ということになります。後半部分は、 $\frac{\pi}{2}\leqq x\leqq \pi$ なので、「微分して $-\cos x$ になるもの」になります。よって、それぞれの積分区間で考えれば、絶対値を外すことができるようになります。計算結果は次のようになります。
\begin{eqnarray} & & \int_0^{\pi} |\cos x| dx \\[5pt] &=& \int_0^{\frac{\pi}{2} } |\cos x| dx+\int_{\frac{\pi}{2} }^{\pi} |\cos x| dx \\[5pt] &=& \int_0^{\frac{\pi}{2} } \cos x dx+\int_{\frac{\pi}{2} }^{\pi} (-\cos x) dx \\[5pt] &=& \Big[ \sin x \Big]_0^{\frac{\pi}{2} }+\Big[ -\sin x \Big]_{\frac{\pi}{2} }^{\pi} \\[5pt] &=& (1-0)+(0+1) \\[5pt] &=& 2 \end{eqnarray}と求められます。

絶対値のついた関数の定積分は何を表している？

【基本】定積分の復習では、定積分と面積が関係していることも復習しました。 $a\leqq x\leqq b$ の範囲で $f(x)\geqq 0$ なら、\[ \int_a^b f(x) dx \]は、 $y=f(x)$, $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積を表すのでした。

ここで、 $y=\cos x$ のグラフを見てみましょう。

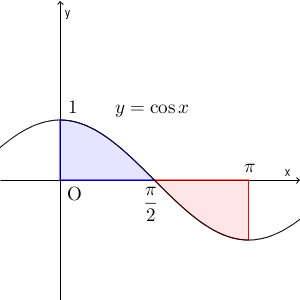
$y=\cos x$ と $x=0$, $x=\pi$, $x$ 軸で囲まれた部分は2つあります。この部分の面積は、\[ \int_0^{\pi} \cos x dx \]では求められません。実際、この定積分を計算すると\[ \Big[ \sin x \Big]_0^{\pi}=0 \]となりますが、明らかにおかしいですね。

先ほどの説明のうち、「$a\leqq x\leqq b$ の範囲で $f(x)\geqq 0$」という条件がすごく大事なんですね。上の図の対象の部分のうち、左側は $x$ 軸より上、右側は $x$ 軸より下です。右側部分が、「 $f(x)\geqq 0$ 」という条件を満たしていないので、「面積が $0$ 」という変な結果が出てしまったんですね。

この右側の部分、つまり、 $x$ 軸より下の部分は、次のように反転して計算すれば求められるようになります。

0以上の部分はそのまま、0以下の部分は反転させる、というのは、まさに「絶対値」ですね。 $|f(x)|\geqq 0$ なので、\[ \int_a^b |f(x)| dx \]は、 $y=f(x)$, $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積（の合計）を表すことになります。

先ほど求めた\[ \int_0^{\pi} |\cos x| dx \]は、 $y=\cos x$ と $x=0$, $x=\pi$, $x$ 軸で囲まれた部分の面積を表すことになるわけです。絶対値がつくと計算が少しめんどくさくなりますが、これはイジワルされているのではなく、数学的に意味のあるものを計算しているんですね。