【基本】定積分の復習
ここでは、以前学んだ定積分の復習をして、これから学んでいく定積分の内容の準備をしていきます。
定積分の復習
定積分は、【基本】定積分で見たように、すでに扱っています。ではなぜまた登場するかというと、対象の関数が広がるからです。以前に定積分について学んだときは、主に二次関数を対象にしていましたが、今回は、もっと幅広い関数を扱います。
以前は、整式に対して定積分を定義しましたが、連続な関数に対しても、次のように定義することができます。
不定積分は、 $x$ についての関数ですが、定積分は、 $F(b)-F(a)$ なので、 $x$ を含まない値になります。
また、不定積分のときには、積分定数 $C$ をつけていましたが、定積分の場合は、\[ (F(b)+C)-(F(a)+C)=F(b)-F(a) \]となるので、積分定数は消えてしまいます。なので、普通は、積分定数を $0$ として計算します。
定積分に出てくる「 $a$ から $b$ まで」という区間を、積分区間といいます。
定積分と面積の関係
定積分を計算して何が出るのか、も復習しておきましょう。【基本】面積と整式の不定積分で登場した、次の図を見てみましょう。
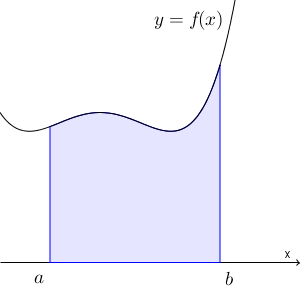
$y=f(x)$ が $a\leqq x\leqq b$ の範囲で連続で、つねに $0$ 以上の値をとるとしましょう。このとき、 $y=f(x)$ と $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積を考えてみます。
$a\leqq c\leqq b$ とし、 $x=b$ ではなく $x=c$ までの部分の面積を $S(c)$ という関数で表すことにします。このとき、 $h\gt 0$ として、 $\dfrac{S(c+h)-S(c)}{h}$ について考えてみましょう。これは、面積の変化量を $x$ の変化量で割った式です。

$\dfrac{S(c+h)-S(c)}{h}$ は、2つの長方形の高さ( $c\leqq x\leqq c+h$ での最小値と最大値)の間にあります。ここで、 $h\to 0$ とすると、2つの高さは近づいていき、どちらも $f(c)$ に収束することがわかります。つまり、面積を微分すると元の関数になる、ということです。面積も不定積分の1つである、ということです。
$f(x)$ の不定積分の1つを $F(x)$ とすると、 $S(x)=F(x)+C$ と書けます。 $b=a$ のときの面積は $0$ であることから、 $C=-F(a)$ なので、\[ S(b)=F(b)-F(a) \]が成り立ちます。この式は、「 $y=f(x)$ と $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積」が定積分で表されることを示しています。
このあたりの話は、【基本】面積と整式の不定積分や【基本】定積分で取り上げています。
定積分の性質
定積分の計算でよく使う、基本的な性質をまとめて紹介します。【基本】定積分の性質でも紹介している内容ですが、対象の関数が広くなっています。
\begin{eqnarray} & & \int_a^a f(x) dx = 0 \\ & & \int_b^a f(x) dx = -\int_a^b f(x) dx \\ & & \int_a^b f(x) dx = \int_a^c f(x) dx+\int_c^b f(x) dx \end{eqnarray}
これらは、不定積分に変換して示すことができます。証明は、【基本】定積分の性質での内容と同じです。
定積分の計算例
以前定積分を学んだときには、次のような二次関数のを扱っていました。
\begin{eqnarray}
& &
\int_0^1 x^2 dx \\[5pt]
&=&
\Big[ \frac{1}{3}x^3 \Big]_0^1 \\[5pt]
&=&
\frac{1}{3}
\end{eqnarray}ただ、今となっては、いろんな関数の不定積分を求められるようになったので、次のような定積分を求めることもできるようになったわけです。
\begin{eqnarray}
& &
\int_0^1 \sqrt{x} dx \\[5pt]
&=&
\Big[ \frac{2}{3}x^{\frac{3}{2} } \Big]_0^1 \\[5pt]
&=&
\frac{2}{3}
\end{eqnarray}このように、いろんな関数の定積分を計算する方法を、しばらく見ていくことになります。
ちなみに、この計算と面積の関係について見てみましょう。先ほども見た通り、定積分は面積を計算していることとつながっているのでした。今行った定積分の計算は、 $y=\sqrt{x}$ と $x=1$ と $x$ 軸で囲まれた部分の面積、つまり、下の図の赤の部分の面積を求めたことになります。

一方、その前に求めた、 $x^2$ の定積分は、放物線 $y=x^2$ と $x=1$ と $x$ 軸で囲まれた部分の面積、つまり、下の図の青の部分の面積です。
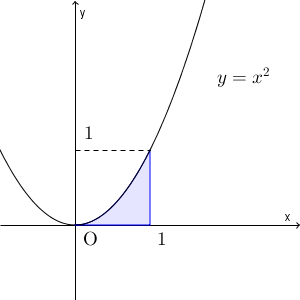
この放物線を $y=x$ で反転すれば、 $y=x^2$ は $x=y^2$ のグラフに変換されます。つまり、この青い部分は、 $y=\sqrt{x}$ のグラフでいうと、次の青い部分に対応することがわかります。

青い部分と赤い部分の面積を足すと、1辺の長さが1の正方形の面積になるはずで、 $\dfrac{1}{3}+\dfrac{2}{3}=1$ なのだから、たしかにそうなっていますね。
おわりに
ここでは、定積分の復習を行いました。不定積分の計算を踏まえて、これからいろいろな定積分の計算を行っていきます。





