【標準】円の接線と作図

ここでは、円の接線に関連する作図の問題を見ていきます。

円の接線の復習

円の接線に関連する問題を見る前に、円の接線について、少し振り返っておきます。【基本】円の接線の作図で見た内容です。

円の接線とは、円と1点だけを共有する直線のことです。

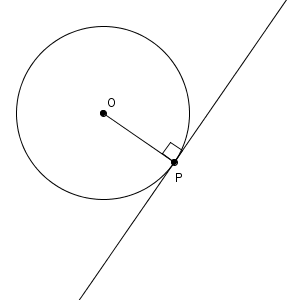
このときに共有する点（上の図では点 P）のことを接点といいます。

また、円の中心と接点を結んだ線分（半径）は、接線と垂直になります。これが円の接線が持つ重要な性質です。

これらを踏まえて、以下の問題を見ていきます。

接線と円の中心から円を作図

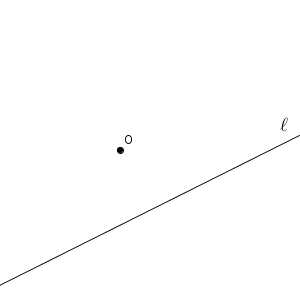
【基本】円の接線の作図では、円から接線を作図する問題を見ましたが、今回は、接線から円を作図する問題です。

円をかくには中心と半径が必要ですが、中心がすでに分かっています。なので、半径がわかればいいですね。接点がわかればいい、ということもできます。どのように作図すればわかるでしょうか。

ここで、接線の持つ性質を利用します。円の中心と接点とを結んだ線分は、接線と垂直となります。ということは、点 O から、直線 $\ell$ に垂線をおろせば、交点が接点となります。【基本】垂線の作図（直線上にない点を通る）その２で見た内容などを使えば、垂線を作図することができるので、次のようにして円を作図することができます。

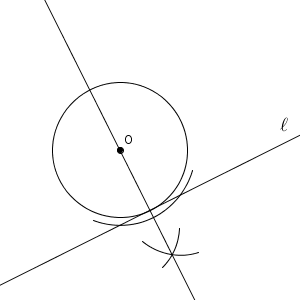
円の中心から接線までの距離は、中心から接点までの距離と等しく、さらに円の半径とも等しくなります。

2つの接線と接点から円を作図

接線が2つと接点がわかっています。どのように作図するかは置いておいて、完成図を考えてみると、次のようになります。

いろいろな性質も合わせて図にかきこみました。これを見ながら、どうすれば作図できるか考えてみましょう。接点がわかっているので、円の中心がわかればいいですね。2つの接線と円の中心はどのような関係になっているでしょうか。

2つの半直線に接するということは、2つの接線からの距離が等しい、と言い換えることもできます。2つの直線からの距離が等しい点の集まりは、角の二等分線となります（参考：【基本】点と直線との距離と作図）。つまり、円の中心は、角の二等分線上にあります。

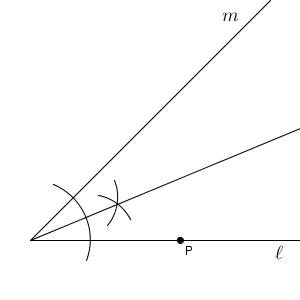
さらに、先ほどの例題でも用いましたが、接点では半径と垂直になることも使いましょう。接点を通り接線に垂直な直線もひきます。

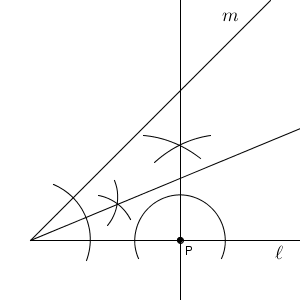
この交点が点 O となります。円の中心がわかったので、円が作図できます。

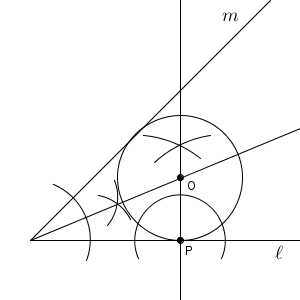
「半径」を「円の中心から接点までの距離」「円の中心から接線までの距離」と言い換えて考えることが重要になってきます。

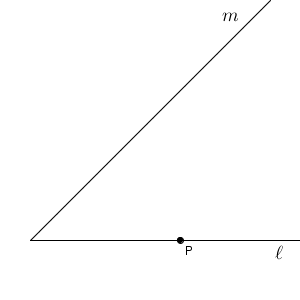
接線と接点と通る点から円を作図

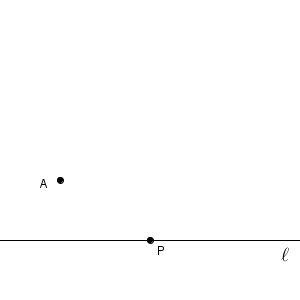
この問題も、完成図から考えましょう。次のようになります。

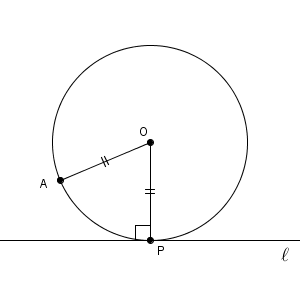
今度も、円の中心がわかればいいですね。まず、半径と接線が垂直であることを使いましょう。点 P を通り、直線 $\ell$ に垂直な直線をひけば、この直線上に円の中心があることがわかります。【基本】垂線の作図（直線上の点を通る）の内容を使います。

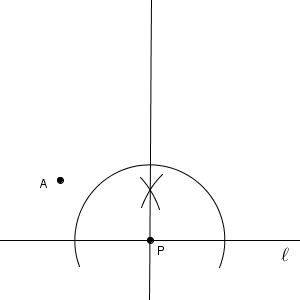
直線 $\ell$ に垂直な直線をかきました。このどこかに円の中心があるはずですが、それはどのように作図すればいいでしょうか。まだ使っていない条件は、「点 A を通る」ですね。これをどのように使えばいいでしょう。

円が通る点は、2点あります。点 A と点 P です。接点も円周上の点なので、点 P も通りますね。これは、言い換えると、中心から点 A, P までの距離は等しい、ということです。このような考え方は、【標準】3点を通る円の作図でも使いました。

このことから、円の中心は、線分 AP の垂直二等分線上にあることがわかります。

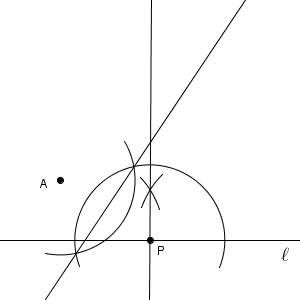
よって、「点 P を通り、直線 $\ell$ に垂直な直線」と「線分 AP の垂直二等分線」との交点が、円の中心であることがわかります。最終的には、次のような図となります。

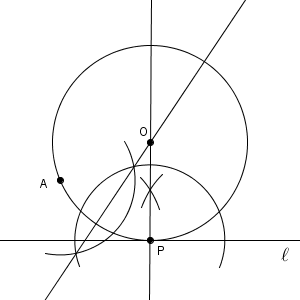
作図で用いるものは、よく使うものは垂線、角の二等分線、垂直二等分線くらいで、数は少ないのですが、いろいろ組み合わせて作図をする必要があります。

おわりに

ここでは、円の接線に関連する作図の問題を見てきました。円の半径を、中心から接点までの距離と考えたり、中心から接線までの距離と考えることで、何を作図すればいいかを考えてきました。完成図から何を作図すればいいか想像すると、考えやすいでしょう。